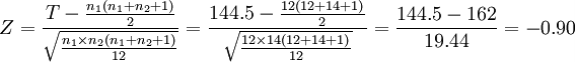rank sum test 秩和检验

秩和检验方法最早是由维尔克松(Wilcoxon)提出，叫维尔克松两样本检验法。后来曼—惠特尼将其应用到两样本容量不等(n1不等于n2)的情况，因而又称为曼—惠特尼U检验。这种方法主要用于比较两个独立样本的差异。

1、假设中的等价问题

设有两个连续型总体, 它们的概率密度函数分别为：

f₁(x),f₂(x)(均为未知)

已知f₁(x) = f₂(x − a)，a为末知常数，要检验的各假设为：

H₀:a = 0,H₁:a < 0.

H₀:a = 0,H₁:a > 0.

H0:a=0,H1, a<>0.

设两个总体的均值存在，分别记为μ₁,μ₂，由于f₁,f₂最多只差一平移，则有μ₂ = μ₁ − a。此时, 上述各假设分别等价于：

H₀:μ₁ = μ₂,H₁:μ₁ < μ₂

H₀:μ₁ = μ₂,H₁:μ₁ > μ₂

H₀:μ₁ = μ₂,H₁:μ_1<>μ₂

2、秩的定义

设X为一总体，将容量为n的样本观察值按自小到大的次序编号排列成x₍₁₎ < x₍₂₎ < Λ < x_(n),称x_(i)的足标i为x_(i)的秩，i = 1,2,Λ,n。

例如：某施行团人员的行李重量数据如表：

重量（kg）
34  39  41  28  33

写出重量33的秩。

因为28<33<34<39<41，故33的秩为2。

特殊情况：

如果在排列大小时出现了相同大小的观察值, 则其秩的定义为足标的平均值。

例如: 抽得的样本观察值按次序排成0,1,1,1,2,3,3,

则3个1的秩均为(2+3+4)/3=3.

两个3的秩均为(6+7)/2=6.5.

3、秩和的定义

现设1，2两总体分别抽取容量为n₁,n₂的样本，且设两样本独立。这里总假定 n1<>n2。

我们将这n₁ + n₂个观察值放在一起，按自小到大的次序排列，求出每个观察值的秩，然后将属于第1个总体的样本观察值的秩相加，其和记为R₁，称为第1样本的秩和，其余观察值的秩的总和记作R₂，称为第2样本的秩和。

显然，R₁和R₂是离散型随机变量，且有R₁+R₂=( (n1+n2)(n1+n2+1) )/2.  

4、秩和检验法的定义

秩和检验是一种非参数检验法, 它是一种用样本秩来代替样本值的检验法。

用秩和检验可以检验两个总体的分布函数是否相等的问题

 

秩和检验的适用范围

如果两个样本来自两个独立的但非正态获形态不清的两总体，要检验两样本之间的差异是否显著，不应运用参数检验中的T检验，而需采用秩和检验。

 

秩和检验的方法

1、两个样本的容量均小于10的检验方法

检验的具体步骤：

第一步：将两个样本数据混合并由小到大进行等级排列（最小的数据秩次编为1，最大的数据秩次编为n₁ + n₂）。

第二步：把容量较小的样本中各数据的等级相加，即秩和，用T表示。

第三步：把T值与秩和检验表中某α显著性水平下的临界值相比较，如果T₁ < T < T₂，则两样本差异不显著；如果T<>T1或T>=T2, 则表明两样本差异显著。

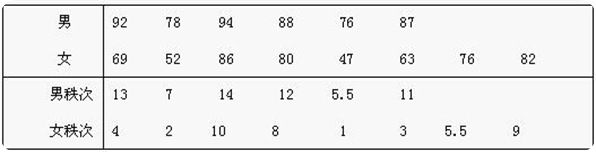
例：某年级随机抽取6名男生和8名女生的英语考试成绩如表1所示。问该年级男女生的英语成绩是否存在显著差异？

男、女生英语考试成绩表

解：检验步骤：

（1）建立假设：

H₀：男女生的英语成绩不存在显著差异

H₁：男女生的英语成绩存在显著差异

（2）编排秩次，求秩和：

T= 13 + 7 + 14 + 12 + 5.5 + 11= 62.5

（3）统计推断：根据n₁ = 6,n₂ = 8,α = 0.05， 查秩和检验表，T的上、下限分别为T₁ = 29,T₂ = 61，有T > T₂，结论是：男女生的英语成绩存在显著差异。

3、两个样本的容量均大于10的检验方法

当两个样本容量都大于10时，秩和T的分布接近于正态分布，因此可以用Z检验，其基本公式为：

式中：T为较小的样本的秩和。

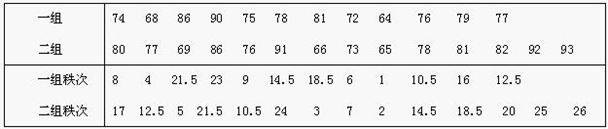
例:某校演讲比赛后随即抽出两组学生的比赛成绩如表2，问两组成绩是否有显著差异？

解：检验步骤：

（1）建立假设：

H₀：两组成绩不存在显著差异

H₁：两组成绩存在显著差异

（2）编排秩次，求秩和：

n₁ = 12,n₂ = 14,T = 144.5，代入公式，有：

（3）统计推断：因为|Z|<1.96，则应保留虚无假设，拒绝备择假设。结论是：两组的演讲比赛成绩不存在显著差异。

 

http://wiki.mbalib.com/wiki/%E7%A7%A9%E5%92%8C%E6%A3%80%E9%AA%8C

http://www.mipang.com/blog/381684.94d.htm

http://baike.baidu.com/view/1889901.htm