滑动窗口的最大值

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

 

进阶：

你能在线性时间复杂度内解决此题吗？

 

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:

滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

方法一：双向队列

前面好多人都讲了双向队列，我这里根据大佬们的解法，总结几点如下
我们通过构建双向队列记录索引并进行如下的操作：
我们将窗口逐渐地向右移。
1.当队列不空且当前队头索引不在窗口内时，pop_front();
2.当队列不空且队尾索引对应的值小于当前值时，pop_back();
3.将当前地索引插入队尾。
4.返回队首元素为此时窗口内地最大值地索引
几点解释：
1.为什么上面地第二点可以删掉队尾地元素？
因为如果后来的索引对应的元素会在较后的时间内滑出窗口，所以比现在进来的元素小的就不可能再成为最大值。
2.为什么检查划出窗口元素的元素只检查队首？
因为队列中的元素按时间先后排序
3.为什么时间复杂度为O(N)？
因为对于每一个索引，他最多进入队列一次，出队列一次。

class Solution {

public:

    //双向队列

    deque<int> dep;

    void clean_queue(int idx,int i,vector<int>& nums){

        if(!dep.empty()&&idx==dep.front())dep.pop_front();

        while(!dep.empty()&&nums[dep.back()]<nums[i])dep.pop_back();

        dep.push_back(i);

    }

    vector<int> maxSlidingWindow(vector<int>& nums, int k) {

        vector<int> res;

        for(int i=0;i<k;i++){

            clean_queue(i-k,i,nums);

        }

        res.push_back(nums[dep.front()]);

        for(int i=k;i<nums.size();i++){

            clean_queue(i-k,i,nums);

            res.push_back(nums[dep.front()]);

        }

        return res;

    }

};

 

方法二 动态规划

算法的思想是将输入数组分割成有 k 个元素的块。
若 n % k != 0，则最后一块的元素个数可能更少。

 

 

 

开头元素为 i ，结尾元素为 j 的当前滑动窗口可能在一个块内，也可能在两个块中。

 

 

 

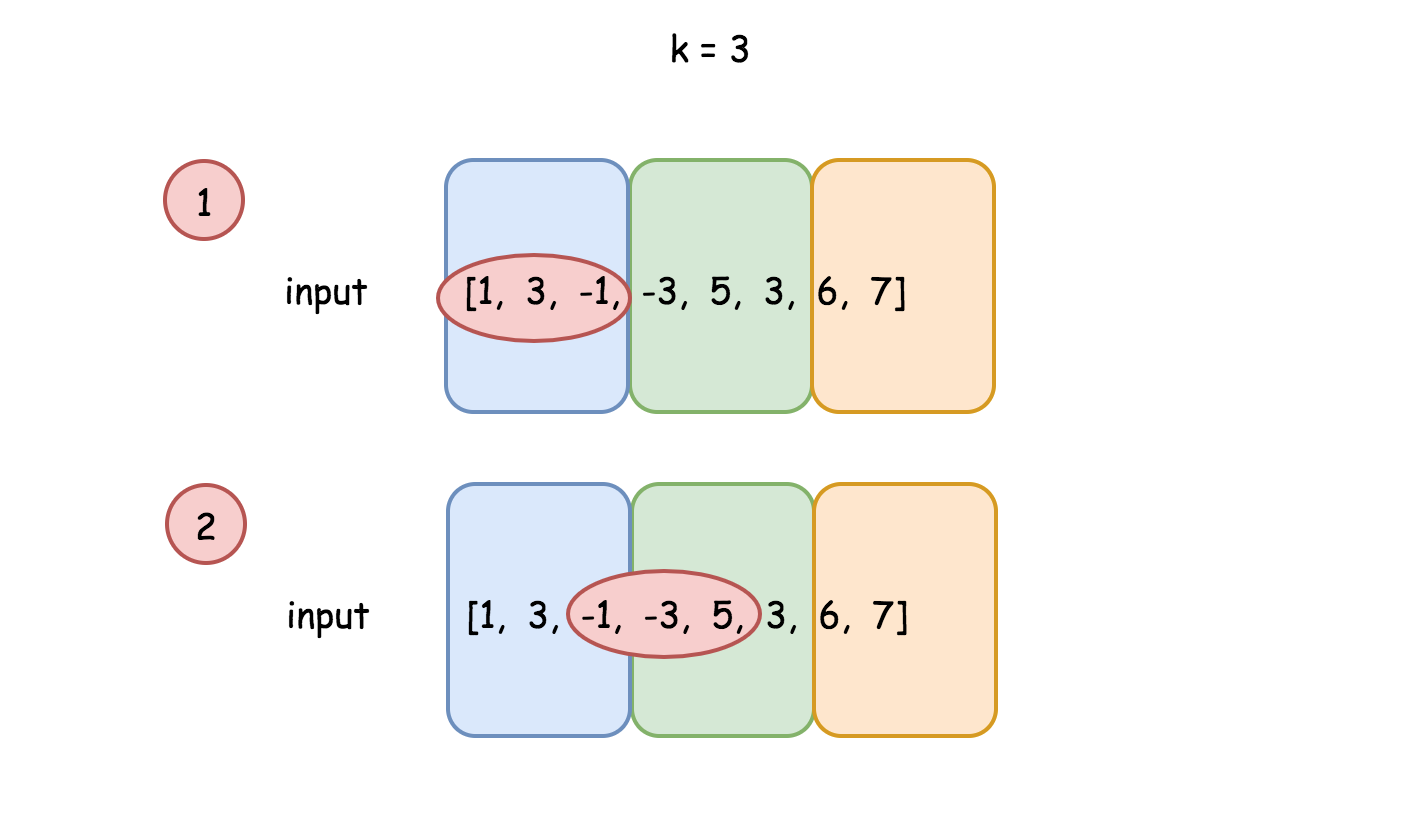
情况 1 比较简单。 建立数组 left， 其中 left[j] 是从块的开始到下标 j 最大的元素，方向 左->右。

 

 

 

为了处理更复杂的情况 2，我们需要数组 right，其中 right[j] 是从块的结尾到下标 j 最大的元素，方向 右->左。right 数组和 left 除了方向不同以外基本一致。

两数组一起可以提供两个块内元素的全部信息。考虑从下标 i 到下标 j的滑动窗口。 根据定义，right[i] 是左侧块内的最大元素， left[j] 是右侧块内的最大元素。因此滑动窗口中的最大元素为 max(right[i], left[j])。