分布式快照算法—— Chandy-Lamport 算法的证明

状态和事件的定义：

对于分布式流处理系统，我们可以将数据处理流程抽象化为DAG（V,E），其中V表示逻辑的处理进程p，E表示进程之间通信的c。

C的状态是沿C发送的消息序列，不包括沿C接收的消息。P的状态是各种参数的值。

流程由一组状态，一个初始状态（来自此组）和一组事件定义（全局状态转换图）。进程p中的事件e是一种原子动作，它可以改变p本身的状态以及最多一个与p进行通信的通道c的状态：c的状态可以通过沿c的发送消息来改变（如果c中的消息由p发出）或沿c接收消息（如果c中的消息是发给p的）。事件e的定义是：（1）事件发生的进程p；（2）事件发生之前p的状态s；（3）事件发生之后p的状态s'；（4）通道c（如果有的话），其状态因事件而改变；以及（5）消息M（如果有的话）沿着c发送或沿着c接收 。我们用5元组（p，s，s’，M，c）定义e，如果e的出现不会改变任何通道的状态，则M和c是特殊符号nul。

分布式系统的全局状态是一组进程和通道的状态：对于初始全局状态，每个进程状态是其初始状态，每个通道的状态为空序列。事件的发生可能会更改全局状态。令事件e =（p，s，s'，M，c）我们说e可以在全局状态S下发生，当且仅当（1）全局状态S下的过程p的状态为s且（2）如果c为指向p的信道，则全局状态S中的c状态是一个消息序列，其头部为M。我们定义一个next函数，其中next（S，e）是在全局状态S中事件e刚发生之后的全局状态。仅当事件e可以在全局状态S中发生时，next（S，e）的值才被定义。 ，在这种情况下，next（S，e）是与S相同的全局状态，除了：（1）next（S，e）中p的状态为s'； （2）如果c是指向p的信道，则next（S，e）中c的状态是S中c将头部的M删除后的状态； （3）如果c是指离p的信道，则next（S，e）中c的状态与S中的c将M添加到c的尾部后的状态。

一个简单的例子：

 

 

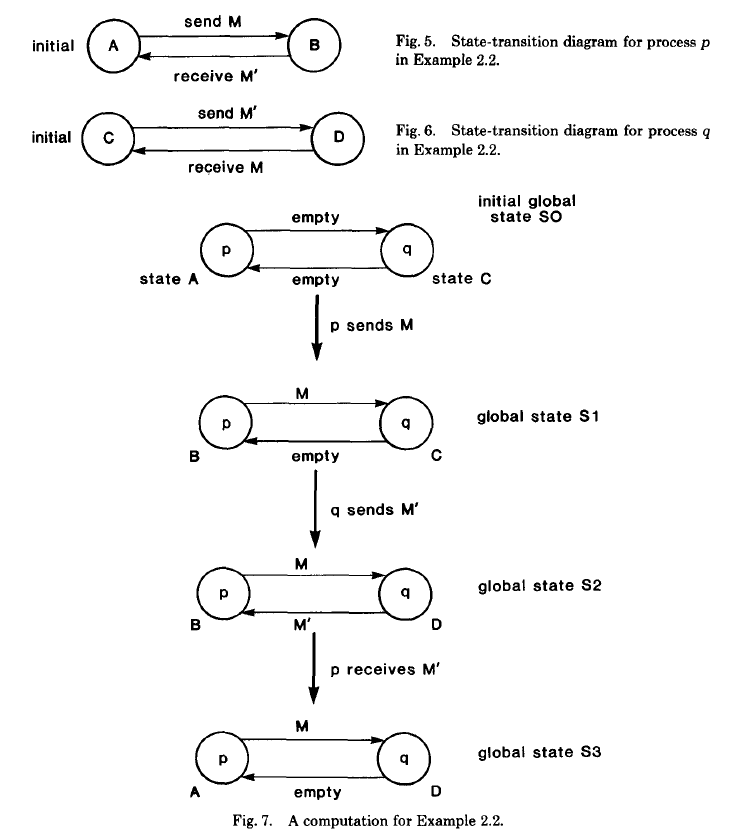
算法：

Motivation for The Steps of the Algorithm
将状态的记录者分为三个角色：

消息的发送者；
消息通道（单向）；
消息的接收者；
消息的发送者同时也可以是消息的接收者，实际过程中消息通道也可能是双向的，都不响应算法描述。接下来原文通过对模型篇中描述的两个模型进行案例分析, 讲了两个道理：

发送者record状态时，已发送的消息数 = channel Record时已经接收消息数。道理不难，场景：A村上午09:00找个拖拉机把大米拉到B存去。

假设1：8:50时，拖拉机司机在小本本上写了一句：“车上没米”；9:01分大米上车，然后A村在自己的小本本上记录了“米已经送离我村”。将两个小本本合起来一看，MD，大米呢。很显然，大米送上车后，拖拉机上的小本本必须得更新了。
同理，A村如果08:59分记小本本，拖拉机09:01分记小本本，就会出现两个小本本上都写着此处有大米了。
同理，接收者record状态时，已经接收的消息数 = channel Record状态时已经被消费的消息数。

 

Global-State-Detection Algorithm Outline
直接给出了一个满足上述条件的算法。有一个重要的前提，大家Record状态的时机是自发的、随机的。具体方式是：

对发送者p：在p记录状态后，发送其他消息前，发送一个marker；
对于接收者q，在其接收到marker时：
如果q未record状态，就记录当前状态，记录channel的状态为空；
如果q已经record了状态，就记录channel的状为当前收到的数据 - q record时已经收到的数据。嘛意思？可以理解为q Record时channel状态的补充记录。
初次看原文的时候，其实觉得这个结论来的有点懵，后来又觉得没毛病：

Channel本身是没有程序载体的，也就是说它不可能记录自己的状态；
谁能轻松的、准确的 Record Channel的状态呢？必然是接收者，如果用发送者，还得有个机制知道下游消费到哪了不是？这种机制一般还会耦合业务。
用Marker来协调发送者和接收者，是利用了发送者和接收者之前必然存在的因果关系，只有数据发送了，接收者才能收到，并且保序。
Channel状态记录的时机虽然是随机的，但是可以通过Marker收到后进行补充，达到满足前一节的两个相等条件。
并不是Record后全局状态就形成了，然是要marker消息走完数据处理全链路之后才会形成。

Termination of Algorithm
为了确保全局状态记录算法在有限时间内终止，每个进程必须确保（L1）没有标记永久保留在发送通道中，并且（L2）在算法启动的有限时间内记录其状态。

如果对于每个进程q：q可以自发记录其状态，或者存在从进程p（自发记录其状态）到q的路径，则可以确保在有限时间内终止。

How to get the global state:

我们将分布式状态记录为S*将seq(ei)定义为一组事件，将Si定义为在ei发生之前的全局状态，那么我们假设分布式状态记录从Sl开始，结束于St,那么对于seq(ei)的子序列seq’(ej),其中t>j>=l，存在一个seq’’(ek)，使得seq’’(ek)是seq’(ej)的子序列，且存在某一个t=>k>=l，使得Sk=S*。

我们将seq’(ej)中的事件分为两类，对于事件e和他所属的进程p,如果事件e发生在p记录自己状态之前，我们称e为前事件，否则我们称e为后事件。我们可以发现如果ej-1为后事件且属于进程p，而ej为前事件且属于进程q，那么事件ej-1和ej不可能对应于这样的一个事件组，即从消息从p发出然后由q接收。假设成立，那么p在记录自己的状态后会发送mark，然后发送消息M，这时q会先收到mark然后再收到M，这意味着ej是一个后事件。

这样，对于所有这样的ej和ej-1，他们之间不存在有序的关系，即我们将这两个事件的发生顺序交换后，Sj+1不会受到任何的影响。这样，我们将seq’(ej)中所有的前事件移动到事件队列seq的前部分（你可以想象是赋予所有的前事件1，赋予所有的后事件0，然后冒泡排序）。

假设最后一个前事件为ek,那么我们可以证明S*=Sk+1。

要证明上述的结论必须要证明：

（1）      经过seq(ei……ek)之后得到能得到S*中所有进程的状态，这是显而易见的，因为所有进程记录状态的时间都在“后事件”之前，而这些后事件我们还没有执行。

（2）      S *中每个通道c的状态为（所有前事件中发送到c的消息）-（所有前事件中从c接收的消息）。我们从两个方面来看c的状态，一方面，我们记录的局部的c的状态是p记录自己状态后到q收到mark之前的所有消息，也就是说，p已经发送的认为q应该处理完的消息减去q实际上处理完了的消息；另一方面（所有前事件中发送到c的消息）-（所有前事件中从c接收的消息）=p发送mark之前已经发送的-q记录state之前已经接收的（因为后面的事件都是在记录状态之后发生的，不会对接收数目产生影响）。这个值就表明了p以为q已经处理了的和q实际上已经处理了的消息数目之差。

这样我们通过重新的排列seq’(ei)中的事件的顺序可以得到从初始状态Sl->S*->St的一个状态转移序列，由于我们已经知道了S*(分布式全局状态)，我们只需要记录那些后事件，然后在S*的基础上演绎这些事件就可以得到St,即全局的状态。

看了一天大概就是这个样子吧，这是我的个人理解，如果想看最透彻的解读推荐看一下论文：https://lamport.azurewebsites.net/pubs/chandy.pdf