[hdu3068]最长回文(Manacher算法)

http://acm.hdu.edu.cn/showproblem.php?pid=3068

题目大意：求最长回文串的长度。

解题关键：Manacher算法

引用一个较好的解释

p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;

 

可以这么说，这行要是理解了，那么马拉车算法基本上就没啥问题了，那么这一行代码拆开来看就是

如果mx > i, 则 p[i] = min(p[2 * id - i], mx - i)

否则， p[i] = 1

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

 

 

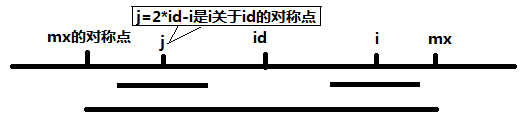
当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。

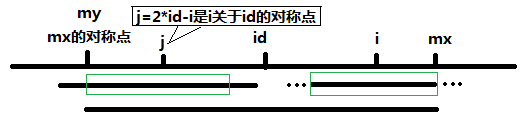
对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
char s[110010*2];
int p[110010*2];
int main(){
    while(scanf("%s",s)!=EOF){
        int len=strlen(s);
        for(int i=len;i>=0;i--){
            s[2*i+1]='#';
            s[2*i+2]=s[i];
        }
        s[0]='*';
        int id=0,maxlen=0;
        for(int i=2;i<2*len+1;i++){
            if(p[id]+id>i) p[i]=min(p[2*id-i],p[id]+id-i);
            else p[i]=1;
            while(s[i-p[i]]==s[i+p[i]])++p[i];
            if(p[i]+i>p[id]+id) id=i;
            if(p[i]>maxlen) maxlen=p[i];
        }
        printf("%d\n",maxlen-1);
    }
}