#410div2C. Mike and gcd problem

C. Mike and gcd problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike has a sequence A = [a1, a2, ..., an] of length n. He considers the sequence B = [b1, b2, ..., bn] beautiful if the gcd of all its elements is bigger than 1, i.e. .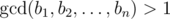

Mike wants to change his sequence in order to make it beautiful. In one move he can choose an index i (1 ≤ i < n), delete numbers ai, ai + 1 and put numbers ai - ai + 1, ai + ai + 1 in their place instead, in this order. He wants perform as few operations as possible. Find the minimal number of operations to make sequence A beautiful if it's possible, or tell him that it is impossible to do so.

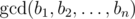 is the biggest non-negative number d such that d divides bi for every i (1 ≤ i ≤ n).

Input

The first line contains a single integer n (2 ≤ n ≤ 100 000) — length of sequence A.

The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.

Output

Output on the first line "YES" (without quotes) if it is possible to make sequence A beautiful by performing operations described above, and "NO" (without quotes) otherwise.

If the answer was "YES", output the minimal number of moves needed to make sequence A beautiful.

 

题解：当$\gcd (x,y)! = 1$时，直接得出答案。

　　　当$\gcd (x,y) =  = 1$，令$d = \gcd (x - y,x + y)$，

　　　所以，$d|(x - y),d|(x + y)$

　　　由信安数基课本P4，$a|b,a|c \to a|tb + sc$,

　　　$d|2x,d|2y$$\to d|\gcd (2x,2y) \to d|2\gcd (x,y) \to d|2$，$d =  = 1or2$因为若再继续下去，必须满足此等式，故不必继续。

　　　可以看出最后的d一定整除偶数,所以n个数必须都为偶数.

　　　所以此题即变为，把n个数变为偶数的最小步数。

　　　当$a[i]\% 2 =  = 1 ，a[i + 1]\% 2 =  = 1$,步数增加1，

　　　当a[i]和a[i+1]有一个为偶数时，步数增加2.

 

 

 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
using namespace std;
ll n,a[100005],t=0;
ll gcd(ll a,ll b){
    while(b){
        ll temp=b;
        b=a%b;
        a=temp;
    }
    return a;
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a[i];
        t=gcd(t,a[i]);
    }
    for(int i=0;i<n;i++){
        a[i]%=2;
    }
    if(t!=1){
        cout<<"YES\n0\n";
        return 0;
    }
    ll ans=0;
    for(int i=0;i<n;i++){
        if(a[i]){
            ans++;
            if(!a[i+1]){
                ans++;
            }
            a[i]=a[i+1]=0;
        }
    }
    cout<<"YES\n"<<ans<<endl;
    
}