力扣题库(随时更新)

1.
"""
给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

"""

def choose(msg):
    lst=[]
    for i in range(len(msg)):
        for j in range(i+1,len(msg)+1):
            m=msg[i:j]
            if len(set(m)) == len(m):
                lst.append(m)
    lst=list(sorted(lst,key=lambda x:len(x)))
    if  len(lst)==0:
        return 0
    return  len(lst[-1])
print(choose(""))
#经测试可以实现功能
#但是超过时间限制

　

def Substring(s):    
　　 st = {}
    i, ans = 0, 0
    for j in range(len(s)):
        if s[j] in st:
             i = max(st[s[j]], i)
         ans = max(ans, j - i + 1)
         st[s[j]] = j + 1
         return ans

　　

　　

 测试 s="abbccd

j=0时

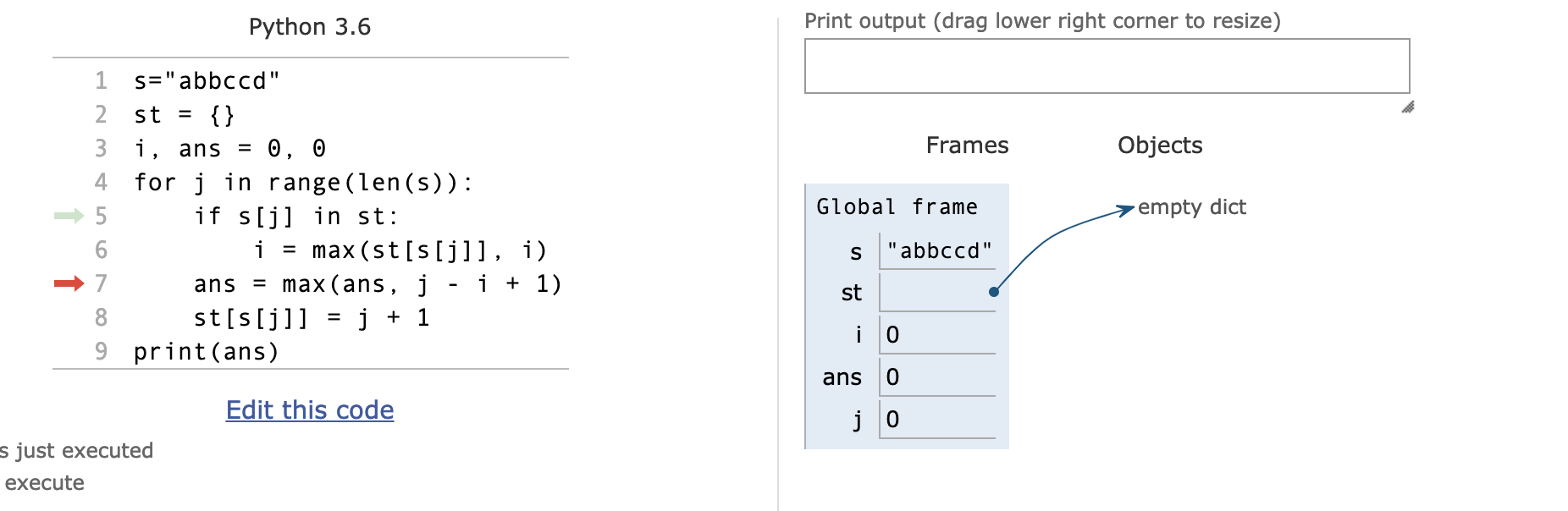
j=1时

 

j=2时

此时循环到s[2]即第二个b

b前面有两个字符,因此 i 被赋值为2

 

 

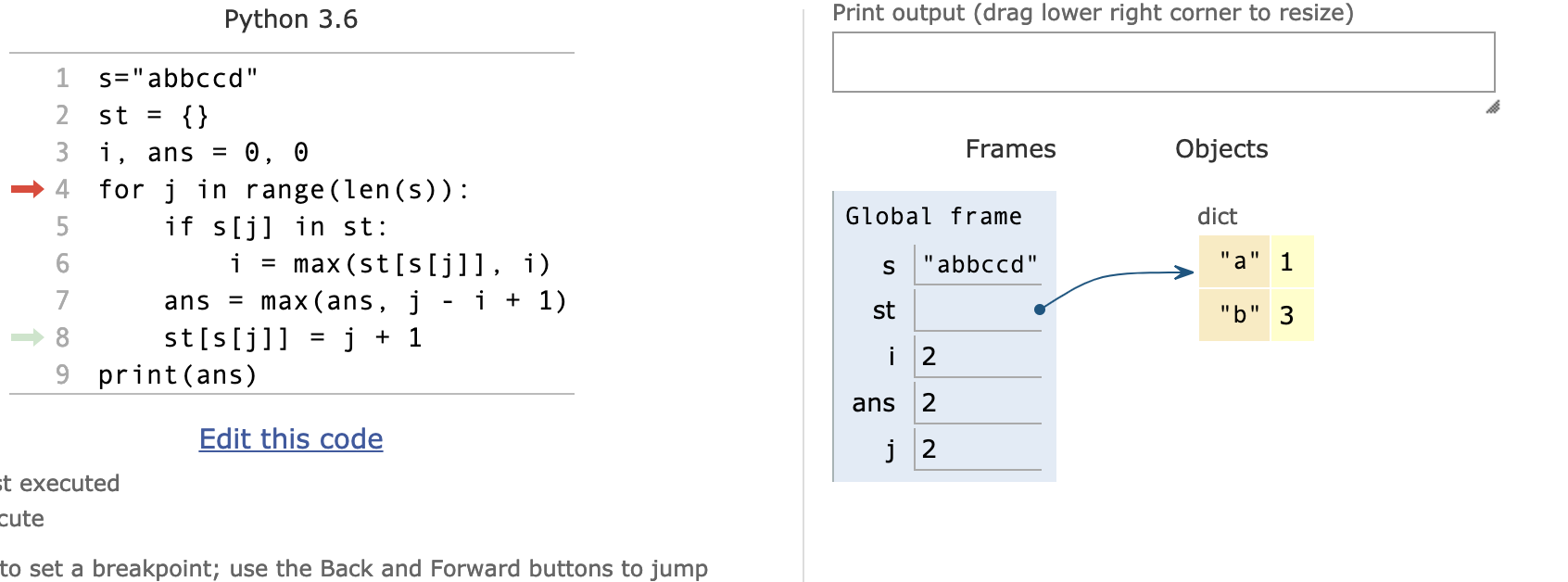
j=3时

 

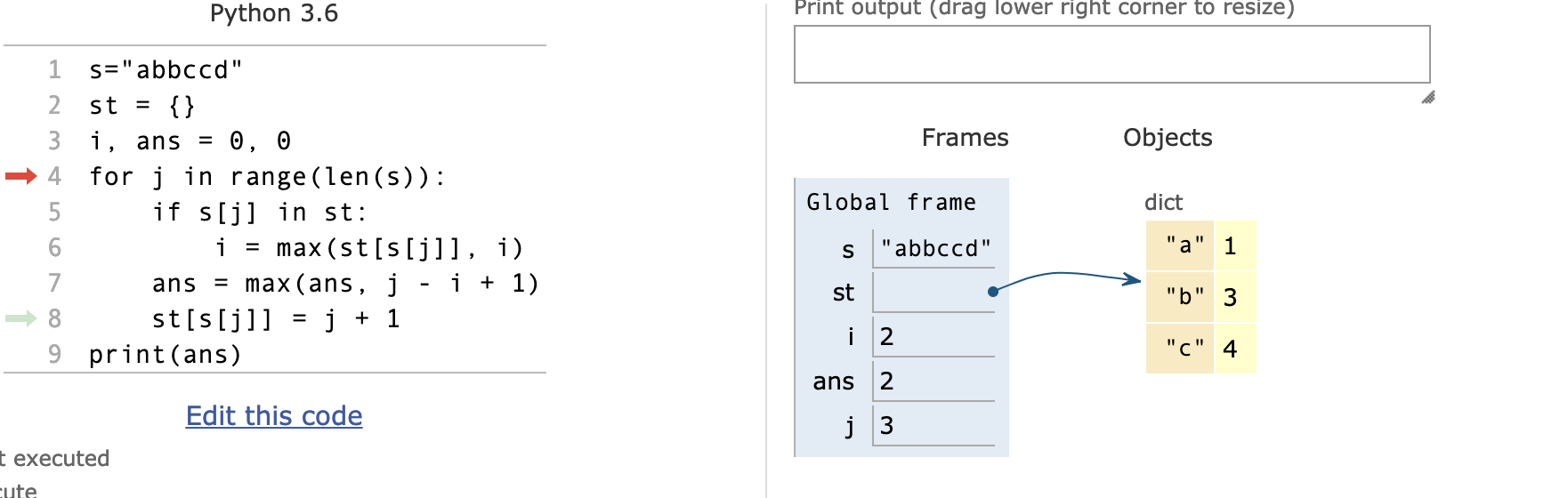
j=4时

此时循环到s[4]即第二个c

c前面有四个字符,因此 i 被赋值为4

 

j=5时 

 

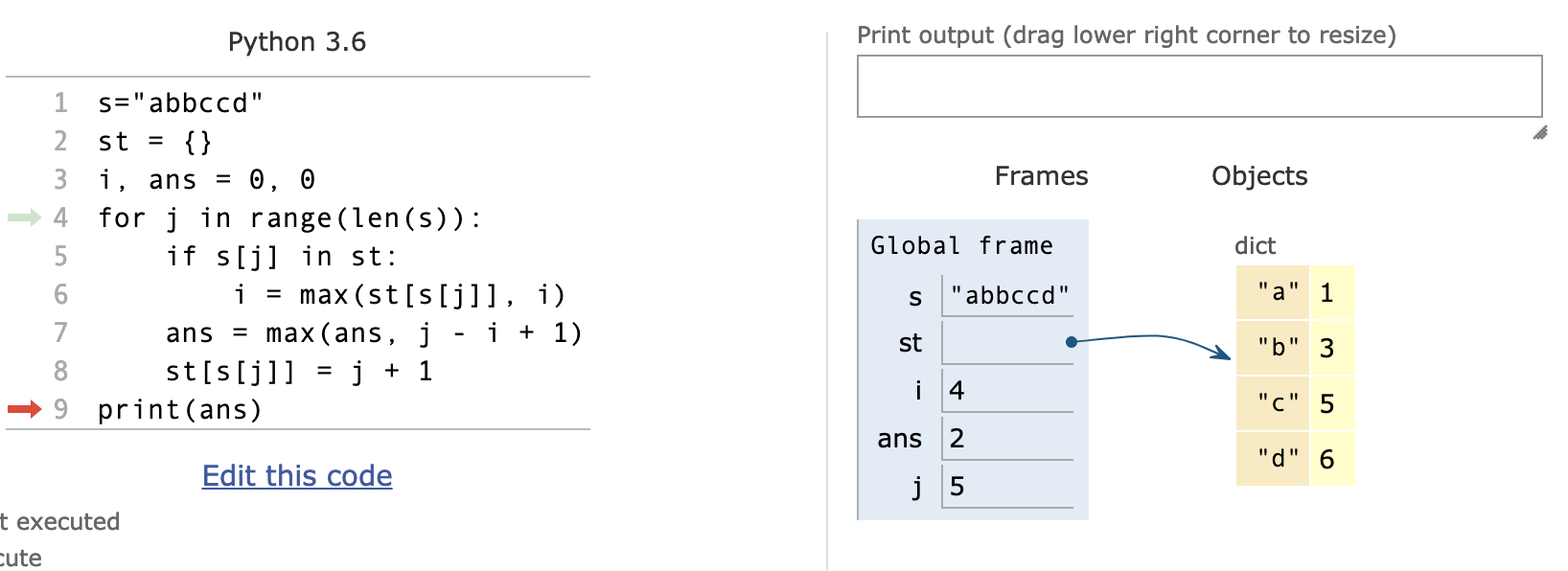
i的作用就是当出现重复字符的时候,把当前字符前面的字符个数赋值给i

ans = max(ans, j - i + 1)

使ans能够在出现重复字符的时候锁定住,直到出现更长的无重复的字符串

 

2.

"""题目描述
输入一行字符串，计算其中A-Z大写字母出现的次数
输入描述:
案例可能有多组，每个案例输入为一行字符串。
输出描述:
对每个案例按A-Z的顺序输出其中大写字母出现的次数。
"""

def socelt(msg):
    import re
    lst=re.findall("[A-Z]",msg)
    return len(lst)

　3.

"""
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
"""

    def findMedianSortedArrays(self, nums1, nums2):
     
        nums1.extend(nums2)
        res = nums1
        if not res:
            return None
        if len(res)==1:
            return res[0]
        res.sort()
        if len(res)%2==0:
            res_ind=int(len(res)/2)

            return (res[res_ind-1] + res[res_ind]) / 2
        else:
            res_ind = int(len(res) //2)
            return res[res_ind]

　　

4.给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

lst=[
    [1,3,1],
    [1,5,1],
    [4,2,1]
]
​

1 2 3 4 5 6 7 8 9 10

rows=len(lst) cols=len(lst[0]) for i in range(rows-2,-1,-1):     lst[i][-1] += lst[i+1][-1] for i in range(cols-2,-1,-1):     lst[2][i] += lst[2][i+1] for i in range(rows-2,-1,-1):     for k in range(cols - 2, -1, -1):         lst[i][k]+=min(lst[i][k+1],lst[i+1][k]) print(lst[0][0])

　　

5.给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分

 

1 2 3 4 5 6 7 8 9 10 11

lst=[      [2],     [3,4],    [6,5,7],   [4,1,8,3] ] cow=len(lst) for i in range(cow-2,-1,-1):     for index in range(0,len(lst[i])):         lst[i][index]+=min(lst[i+1][index],lst[i+1][index+1]) print(lst[0][0])