二叉树

二叉树

• 基本概念

  • 二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”

• 根节点

  • 树中最顶部的节点

• 子树

  • 完整的子树
    • 根节点和左右叶子节点组成
  • 不完整的子树
    • 根节点和左叶子节点
    • 根节点和右叶子节点
    • 根节点
  • 特点：每一个节点都可以作为一棵子树的根节点

• 二叉树节点表示以及树的创建

  # coding:utf-8
  
  class Node:
      '''节点的实现'''
      def __init__(self,item):
          self.item = item
          self.left = None
          self.right = None
  
  
  class Tree:
      '''树'''
      def __init__(self):
          self.root = None
  
      def insert(self,item):
          '''添加节点'''
          node = Node(item)
          #判断树是否为空，如果为空，则将该节点赋值给根节点
          if self.root == None:
              self.root = node
              return
          q = [self.root]
          while q:
              cur = q.pop(0)
              if not cur.left:
                  cur.left = node
                  break
              else:
                  q.append(cur.left)
              if not cur.right:
                  cur.right = node
                  break
              else:
                  q.append(cur.right)

二叉树的遍历

• 树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问，即依次对树中每个结点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（traversal）。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。
• 深度优先遍历（纵向遍历）：按照子树中根节点的位置，可以分为以下3种形式
  • 先序遍历：根节点-左子树-右子树
  • 中序遍历：左子树-根节点-右子树
  • 后序遍历：左子树-右子树-根节点
  • 深度遍历实现思路：
    • 深度遍历是需要作用到每一棵子树中
    • 子树和子树的区别体现在根节点中
    • 如果写一个函数，该函数可以将一棵子树中的节点进行遍历，则将该函数作用其它函数中，就可以实现深度遍历

      def pre_order(self,root):
          '''先序排列'''
          if root == None:
              return
          print(root.item)
          self.pre_order(root.left)
          self.pre_order(root.right)
      
      def middle_order(self,root):
          '''中序排列'''
          if root == None:
              return
          self.middle_order(root.left)
          print(root.item)
          self.middle_order(root.right)
      
      def post_order(self,root):
          '''后序排列'''
          if root == None:
              return
          self.post_order(root.left)
          self.post_order(root.right)
          print(root.item)

• 广度优先遍历（层次遍历）：从树的根节点开始，从上到下，从左到右遍历整个树的节点

  def travel(self):
      '''广度优先遍历'''
      if self.root == None:
          return
      cur = self.root
      q = [cur]
      while q:
          cur = q.pop(0)
          print(cur.item)
          if cur.left:
              q.append(cur.left)
          if cur.right:
              q.append(cur.right)

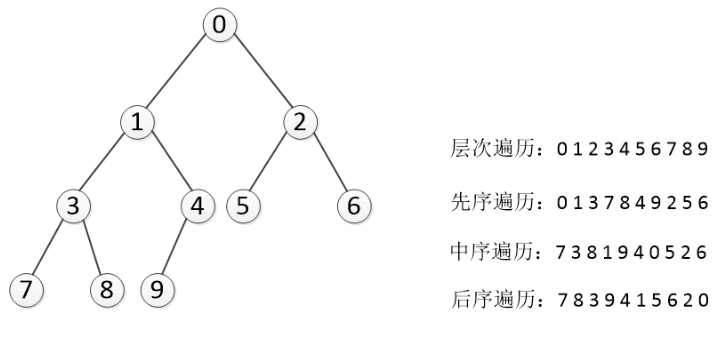
• 示例：
  • 

二叉排序树

• 定义

  • 一棵空树，或者是具有下列性质的二叉树：
    （1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
    （2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
    （3）左、右子树也分别为二叉排序树；

• 排序

  • 通过深度优先遍历中的中序遍历，即可按照升序遍历所有节点元素的值

• 二叉排序树及其排序算法的实现：

  # coding:utf-8
  
  class Node:
      '''节点的实现'''
      def __init__(self,item):
          self.item = item
          self.left = None
          self.right = None
  
  class SortTree:
      '''二叉排序树'''
      def __init__(self):
          self.root = None
  
      def add(self,item):
          '''插入'''
          node = Node(item)
          #如果为空树，则直接赋值给根节点
          if self.root == None:
              self.root = node
              return
          cur = self.root
          while True:
              #插入的值小于根节点的值，则插入到根节点的左侧
              if item <= cur.item:
                  #左节点为空，则直接插入
                  if cur.left == None:
                      cur.left = node
                      break
                  #左节点非空，则将游标指向该节点，然后将值继续与左节点作比较
                  else:
                      cur = cur.left
              #插入的值大于根节点的值，则插入到根节点右侧
              else:
                  #右节点为空，则直接插入
                  if cur.right == None:
                      cur.right = node
                      break
                  #右节点非空，游标指向右节点，然后将值继续与右节点作比较
                  else:
                      cur = cur.right
  
      def middle_order(self,root):
          '''中序排列'''
          if root == None:
              return
          self.middle_order(root.left)
          print(root.item)
          self.middle_order(root.right)
  
  if __name__ == '__main__':
      t = SortTree()
      alist = [3,5,2,4,7,6,9,1,8,0]
      for item in alist:
          t.add(item)
      t.middle_order(t.root)