Q-Learning算法简明教程
声明
本文转载自:https://blog.csdn.net/itplus/article/details/9361915
此处仅作学习记录作用。这篇教程通俗易懂,是一份很不错的学习理解Q-learning算法工作原理的材料。
以下为正文:
1.1 Step-by-Step Tutorial
本教程将通过一个简单但又综合全面的例子来介绍Q-learning算法。该例子描述了一个利用无监督训练来学习位置环境的agent。
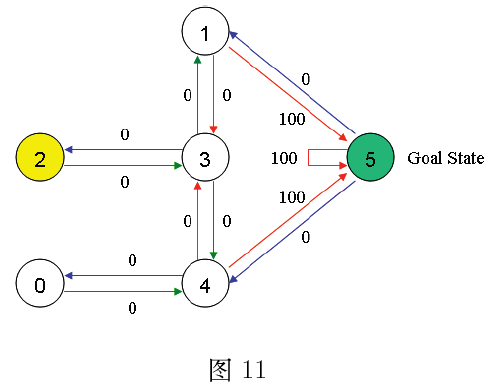
假设一幢建筑里面有5个房间,房间之间通过门相连(如图1所示)。我们将这五个房间按照从0至4进行编号,且建筑的外围可认为是一个大的房间,编号为5。
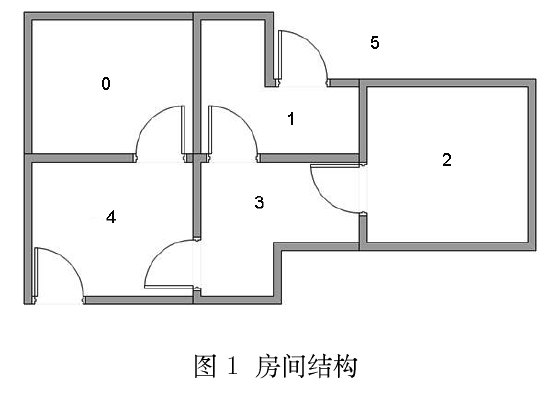
上图的房间也可以通过一个图来表示,房间作为图的节点,两个房间若有门相连,则相应节点间对应一条边,如图2所示。

对于这个例子,我们首先将agent置于建筑中的任意一个房间,然后从那个房间开始,让其走到建筑外,那是我们的目标房间(即编号为5的房间)。为了将编号为5的房间设置为目标,我们为每一扇门(即相应的边)关联一个reward值:直接连接到目标房间的门的reward值为100,其他门的reward值为0。因为每一扇门都有两个方向(如由0号房间可以去4号房间,而由4号房间也可以返回0号房间),因此每一个房间上指定两个箭头(一个指进一个指出),且每个箭头上带有一个reward值(如图3所示)
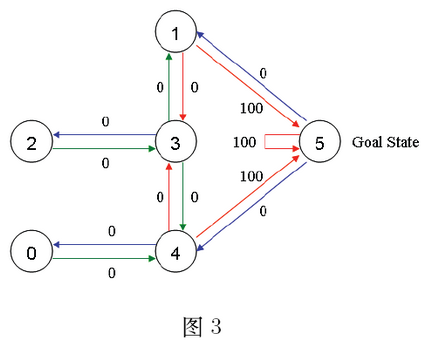
注意,编号为5的房间有一个指向自己的箭头,其reward值为100,其他直接指向目标房间的边的reward值也为100。Q-learning的目标是达到reward值最大的state,因此,当agent到达目标房间后将永远停留在那里。这种目标也称为“吸收目标”。
想象一下,我们的agent是一个可以通过经验进行学习的“哑巴虚拟机器人”,它可以从一个房间走到另一个房间,但是,它不知道周边的环境,也不知道怎么走到建筑的外面去。
下面我们想对agent从建筑里的任意房间的简单撤离进行建模。假定现在agent位于2号房间,我们希望agent通过学习到达5号房间。

Q-Learning算法中有两个重要术语:“状态(state)”和“行为(action)”。
我们将每一房间(包括5号房间)称为一个“状态”,将agent从一个房间走到另外一个房间称为一个“行为”。在图2中,一个“状态”对应一个节点,而一种“行为”对应一个箭头。
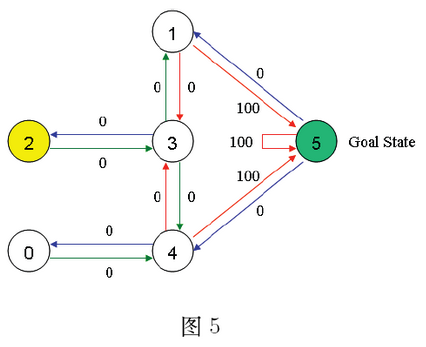
假设agent当前处于状态2。从状态2,它可以转至状态3(因为状态2到状态3有边相连)。但从状态2不能转至状态1(因为状态2到状态1没边相连)。类似地,我们还有
- 从状态3,它可以转至状态1和4,也可以转回至状态2.
- 从状态4,它可以转至状态0,5和3.
- 从状态1,它可以转至状态5和3.
- 从状态0,它只能转至状态4.
我们可以以状态为行,行为为列,构建一个如图6所示的关于reward值的矩阵R,其中得-1表示空值(相应节点之间没有边相连)。

类似地,我们也可以构建一个矩阵Q,它用来表示agent已经从经验中学到的知识。矩阵Q与R是同阶,其行为表示状态,列表示行为。
由于刚开始时agent对外界环境一无所知,因此矩阵Q应初始化零矩阵。为简单起见,在本例中我们假设状态的数目是已知的(等于6)。对于状态数目未知的情形,我们可以让Q从一个元素出发,每次发现一个新的状态时就可以在Q中增加相应的行列。
Q-learning算法的转移规则比较简单,如下式所示:
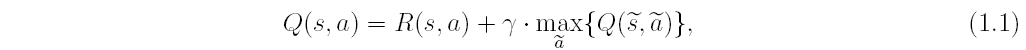
其中s, a表示当前的状态和行为,~s, ~a表示s的下一个状态及行为,学习参数γ为满足0≤γ<1的常数。
在没有老师的情况下,我们的agent将通过经验进行学习(也称为无监督学习)。它不断从一个状态转至另一个状态进行探索,直到到达目标。当agent达到目标状态后,一个episode即结束,接着进入另一个episode。
下面给出整个Q-learning算法的计算步骤。
算法1.1(Q-learning算法)
Step 1 给定参数γ和reward矩阵R。
Step 2 令Q := 0。 # 将表格Q初始化为0
Step 3 For each episode:
3.1 随机选择一个初始的状态s。
3.2 若未达到目标状态,则执行以下几步
(1) 在当前状态s的所有行为中选取一个行为a.
(2) 利用选定的行为a, 得到下一个状态~s.
(3) 按照(1.1)计算Q(s, a)
(4) 令s := ~s
Agent利用上述算法从经验中进行学习。每一个episode相当于training session。在一个training session中,agent探索外界环境,并接收外界环境的reward, 直到达到目标状态。训练的目的是要强化agent的“大脑”(用Q表示)。训练得越多,则Q被优化得更好。当矩阵Q被训练强化后,agent便很容易找到目标状态得最快路径了。
公式(1.1)中的γ满足0≤γ<1. γ趋向与0表示主要考虑immediate reward, 而γ趋向于1表示agent将同时考虑future rewards.
利用训练好的矩阵Q,我们可以很容易地找出一条从任意状态S0出发达到目标状态的行为路径,具体步骤如下:

1.2 Q-Learning Example By Hand
为进一步理解上一节介绍的Q-Learning 算法是如何工作的,下面我们一步一步地迭代几个episode。
首先取学习参数γ=0.8,初始状态为房间1,并将Q初始化为一个零矩阵。
观察矩阵R的第二行(对应房间1或状态1),它包含两个非负值,即当前状态1的下一步行为有两种可能:转至状态3或转至状态5.随机地,我们选取转至状态5

想象一下,当我们的agent位于状态5以后,会发生什么事呢?观察矩阵R的第6行(对应状态5),它对应三个可能的行为:转至状态1,4或5.根据公式(1.1),我们有
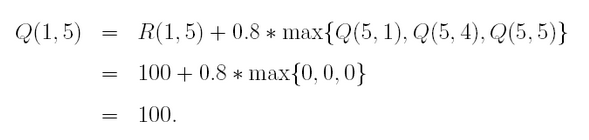
现在状态5变成了当前状态。因为状态5即目标状态,故一次episode便完成了,至此,agent的“大脑”中的Q矩阵刷新为
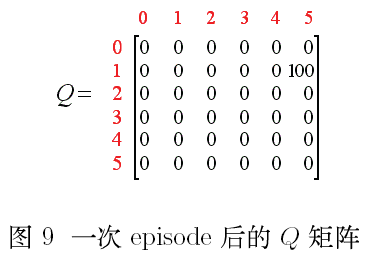
接下来,进行下一次episode的迭代,首先随机地选取一个初始状态,这次我们选取状态3作为初始状态。
观察矩阵R的第四行(对应状态3),它对应三个可能的行为:转至状态1,2或4.随机地,我们选取转至状态1.因此观察矩阵R的第二行(对应状态1)。它对应两个可能的行为:转至状态3或5.根据公式(1.1),我们有

注意到上式中的Q(1,5)用到了图9中的刷新值。此时,矩阵Q变为
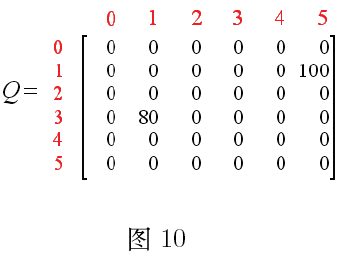
现在状态1变成了当前状态。因为状态1还不是目标状态,因此我们需要继续往前探索。状态1对应三个可能的行为:转至状态3或5.不妨假定我们幸运地选择了状态5.
此时,同前面的分析一样,状态5有三个可能的行为:转至状态1,4或5.根据公式(1.1),我们有

注意,经过上一步刷新,矩阵Q并没有发生变化。
因为状态5即为目标状态,故这一次episode便完成了,至此,agent的“大脑”中的Q矩阵刷新为

若我们继续执行更多的episode,矩阵Q将最终收敛成

对其进行规范化,每个非零元素都除以矩阵Q的最大元素(这里为500),可得(这里省略了百分号)

一旦矩阵Q足够接近于收敛状态,我们的agent便学习到了转至至目标状态的最佳路径。只需按照上一节结尾时介绍的步骤,即可找到最优路径(如图15所示)。

例如,从2为初始状态,利用Q,可得
- 从状态2,最大Q元素指向状态3;
- 从状态3,最大Q元素指向状态1或4(这里假设我们随机地选择了1);
- 从状态1,最大Q元素指向状态5,
因此最佳路径的序列为2-3-1-5.





