CS231N 数据预处理(data proprecessing)

原文链接：https://blog.csdn.net/weixin_38646522/article/details/79534677

 

一些数据预处理的标准方法有均值化数据和归一化数据。

零中心化的意义在上面已经详细的讲述了，这里就不在细讲。

 

 

归一化数据的意义在于让所有的特征都在相同的值域之内，并且让这些特征有相同的贡献。对于图像处理，在大部分情况下会进行零中心化处理，但实际上却不会真的去过多地进行归一化处理像素值。因为一般对图像来说，在每个位置已经得到了相对可比较的范围和分布，所以也没必要去进行归一化处理。

 

 

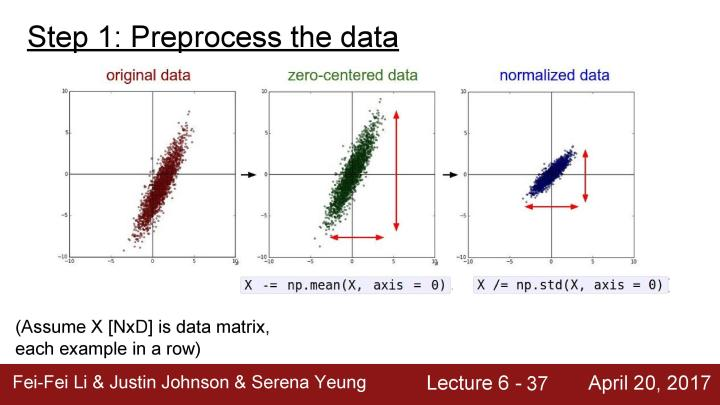
 在机器学习中可能会看到更为复杂的东西，类似PCA或者是whitening（白化），但在图像应用领域就是一直坚持使用零均值化，而一般不做其它复杂的预处理，因为我们不会想要所有的输入投影到一个更为低维度的空间中。

一旦在训练阶段对训练集进行了数据预处理，那么在测试阶段也需要对测试数据做同样的事情。在训练阶段决定的均值也会应用到测试数据中，所以会从训练数据中得到相同的经验均值来进行零均值化预处理。一般对于图像，从训练数据中计算均值图像，每张图像的尺寸都是相同的，然后会得到一组数据并对要传到网络中的每张图减去这组均值，最后对训练数据进行同样的处理。实际上对一些网络也通过减去单通道的均值，来代替用一整张均值图像来将图像数据集零中心化。这么做的原因是对于整张图片来看，减去均值图像和只是减去单通道图像均值相比并没有太大的不同，同时更容易传输和处理，例如你会在VGG网络中看到这样的操作。例如如果网络中使用的是sigmoid函数，数据预处理的零均值化仅仅会在网络的第一层解决了sigmoid函数式非零中心化的问题，因为一般使用的网络都很深，所以在后面的层中这个问题会以更恶化和严重的形式出现。

 

下面讲述关于初始化权值的内容。

 

 

先来个问题，例如有一个标准的双层神经网络，我们看到所有这些用来学习的权值都是需要初始化的，然后再使用梯度更新这些权值，那么这时候使用零初始化的权值会发生什么？这时候全部神经元做的事情都会是一样的，由于权值都是零，给定一个输入，每个神经元将在输入数据上有相同的操作，然后它们将会输出相同的数值并得到相同的梯度，因为这会用相同的方式更新并得到完全相同的神经元。但这不是我们想要的，我们希望不同的神经元学习到不同的知识。

 

 

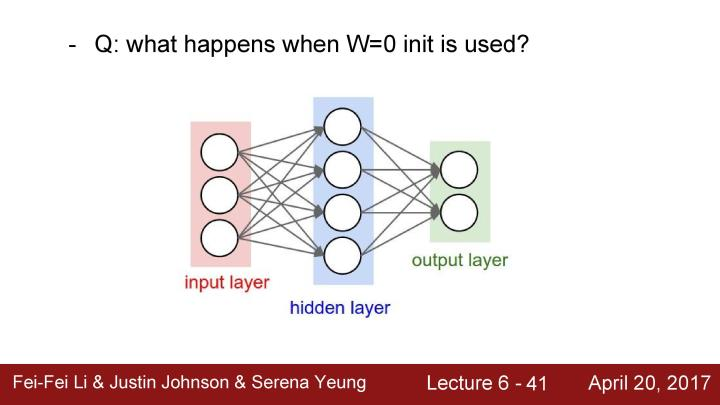
 所以首要做的事情是尝试将其改变为所有的权值初始化为一个很小的随机数，我们可以从一个概率分布中抽样，例如从标准高斯分布中抽样并把抽样结果乘以0.01。这样的初始化在小型的神经网络中表现很好，因为解决了参数对称问题。但在结构较深的神经网络中会存在问题。

下面通过一个试验分析这个问题。这里使用一个结构较深的神经网络，在下面的例子中，初始化了一个有十层的神经网络，每层都有500个神经元，并使用tanh非线性激活函数，用很小的随机数来初始化权值。用随机数据作为输入，在每一层观察中产生的激活函数的数据的统计结果。

可以观察到如果计算每一层的均值和标准差，就可以看到第一层的数据的均值总是在0的附近（应为tanh是以0为中心的），但是标准差会缩小并快速逼近到0，如第二个图所示。如果把结果画出来，下面的折线图显示的是每层的均值和标准差，底部一些列的柱状图是展示了每一层的激活值的概率分布。

 

 

 可以看到在第一层有一个合理的高斯分布，问题是当每一层乘以一些小的随机数的权值W后，激活数值会随着一次次的相乘而迅速地缩小，最后得到的结果全部为零。在反向传播时，每一层都是很小的输入值（都小到近似于0），为了得到对权值的梯度，要用上游的梯度乘以本地的梯度，对W * x节点，本地梯度就是x (已经是很小的输入值），这时的权值梯度结果就会近乎为0，这和之前用零来初始化权值出现的问题类似，这意味着它们基本上是没有更新的。当把所有的梯度连接在一起，由于这个是点积运算，实际上在每一层的反向传播中是在做上游梯度和权值的乘法来得到下游的梯度。所以不断地乘以W会得到类似与正向传播中所有数据变得越来越小的现象（因为正向传播中后面的激活值都是几乎为0），现在梯度和上游梯度都会趋向于0。

 

 

 现在我们知道当权值很小的时候会出现问题，如果尝试使用增大权值来解决这个问题会出现什么？从标准高斯分布中抽象并把抽样结果乘以1，现在的权值都很大，W和X通过这样的网络得到输出，考虑到tanh的特点，如果输入的值是非常大或者非常小，这时网络就总是处于饱和状态。观察下面图中的激活值分布都是趋向于-1或者+1，这会到所有梯度都趋向于0，权值将不会得到更新。

 

可以看到初始化是一个挺苦难的事情，初始化的权值不能太大或者太小，不过一个很好的初始化权值的方法是Xavier initialization。关于这个方法的公式的解释是，如果观察到这里的W，可以看到把它们初始化为从高斯分布中取样，然后根据输入的数量来进行缩放。这个方法的解决问题的原理可以查阅课程对应的notes(http://link.zhihu.com/?target=http%3A//cs231n.github.io/neural-networks-2/%23init), 但基本上的做法是指定输入的方差等于输出的方差，直观地说这种方法是如果有少量的输入，那么就除以较小的数从而得到较大的权值，我们需要较大的权值，假设有少量的输入，用每一个输入值乘以权值，那就需要一个更大的权值来得到一个相同的输出方法，反之亦然。基本上想要一个unit gaussian权值作为每一层的输入，为了可以初始化unit gaussian权值，可以在训练时使用Xavier initialization，所以在每一层大概会有一个unit gaussian。

 

 

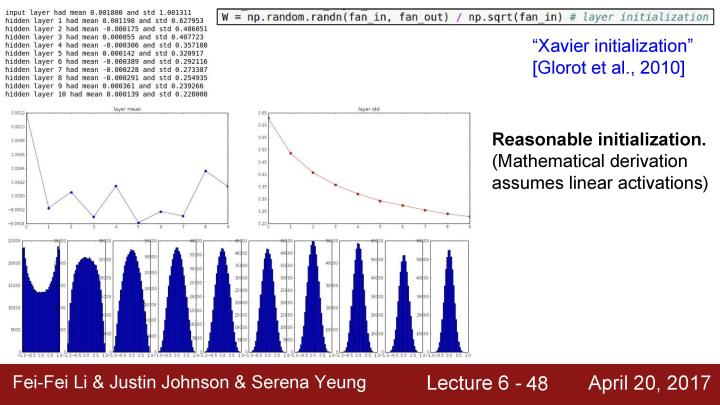
但问题是当使用类似ReLU等激活函数时，因为类似ReLU的激活函数会让一半的神经元挂掉。也就是每次都将有大约一半的神经元被设置为零，实际上这是把得到的方差减半。如果现在假设得到的推导和之前是相同的，那就不会得到正确的方差，而是一个特别小的值。最后将会再次看到unit gaussian分布开始收缩，这时越来越多的峰值会趋向于0。

 

 

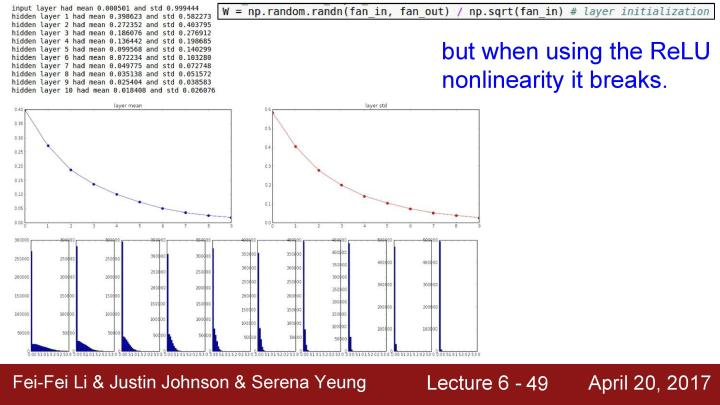
 在一些论文中已经指出可以试着通过除以2来解决这个问题，这些做法基本上是在调整，因为有一半的神经元被设置为0，所以有效的输入只是真实输入的一半，所以只要除了2这个因子，这就很好地解决了这个问题。同时也可以发现unit gaussian分布在深度神经网络中每层都表现得很好。在实践中，重视权值是非常重要的，这会训练结果有很大的影响。

 

 

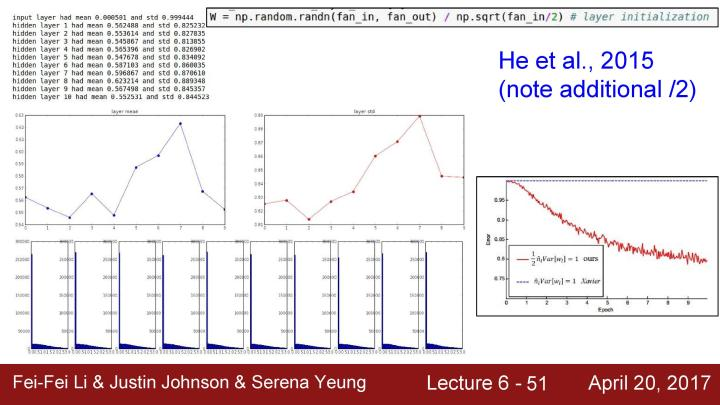
 合理地初始化权值仍然是一个活跃的研究领域，下面是一些这个方面的论文和资源。一个很好的经验法则是从使用Xavier initialization开始，然后再考虑一些其他的方法。

 

接下来要讲述的是Batch Normalization的内容

 

 

 Batch Normalization 的想法是在想要的gaussian范围内保持激活。我们要想unit gaussian激活，那么对它们进行批量归一化。考虑一下在某一层上的批量激活，取目前批量处理的均值，然后可以用均值和方差进行归一化。基本上是在训练开始的时候才设置这个值，而不是在初始化权值的时候设置，这就可以在每一层都有很好的unit gaussian分布和在训练的时候能够一直保持。现在要明确地让所有通过深度神经网络的前向传播在每一层都有很好的unit gaussian分布。通过归一化每一个神经元的输入的这批数据均值和方差来实现这个目的，同时这是一个可微函数。

 

 

如果观察输入的数据，就会想到假设在当前的批处理中有N个训练样本，并假设每个批量处理都是D维度的，然后将对每个维度单独计算经验均值和方差，并且对其进行归一化。

批量归一化通常在全连接或者卷积层之后插入，我们不断地在这些层上乘以权值W，虽然会对每一层造成不好的scaling effect, 但是这基本上可以消除这种影响。因为基本上是通过每个与神经元激活函数相连的输入来进行缩放，所以可以用相同的方法在全连接层和卷积层，唯一的区别是在卷积层的情况下，我们不仅想要归一化所有的训练样例的每个独立的特征维度，而且要联合归一化在激活映射中所有的特征维度、空间位置和所有特性。这么做的原因是想要服从卷积的性质，我们希望附近的位置能够以同样的方式进行归一化。所以在卷积层的情况下，在每个激活图中会有一个均值和方差，我们将在批量处理的所有实例中进行归一化。

 

 

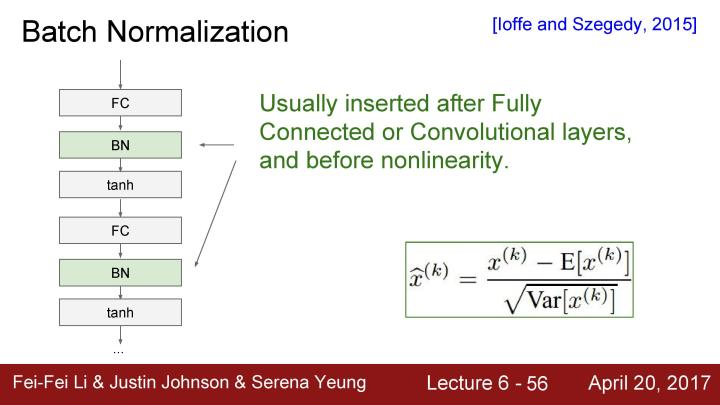
要注意的是我们并不清楚要在每个全连接层之后进行批量归一化的操作，也并不清楚是否确实需要给这些tanh非线性函数输入unit gaussian数据。因为这里所做的是把输入限制在非线性函数的线性区域内，虽然这并不绝对，但基本而言我们是希望避免出现饱和状态，但是有一点饱和状态也是好的，同时你希望能够控制饱和的程度。

 

 

所以要强调的是，批量归一化是在完成归一化操作之后需要进行额外的缩放操作。所以我们先做了归一化，然后使用常量 进行缩放，再用另外一个因子 进行平移，并且这里实际在做的是允许你恢复恒等函数。网络可以按照需要学习缩放因子 使之等于方差，也可以学习 使之等于均值，在这种情况下就可以恢复恒等映射，就像没有进行批量归一化一样。现在就拥有让网络为了达到比较好的训练效果而去学习控制让tanh具有更高或者更低饱和状态的能力。我们希望学习 和 从而恢复恒等函数的原因是想要它具有灵活性，批量归一化做的是将数据转换为unit gaussian数据，虽然这是一个很好的想法，但这不能保证总是最好的选择，在tanh这样的特殊例子中，我们希望可以控制饱和状态的程度，所以这样做是为了让类似进行unit gaussian归一化一样更具备灵活性。

 

 下面是批量归一化的一个小结。

 

 在测试阶段，对批量归一化层，现在减去了训练数据中的均值和方差，所以在测试阶段不用重新计算，只需把这当成训练阶段，例如在训练阶段用到了平均偏移，在测试阶段也同样会有所用到