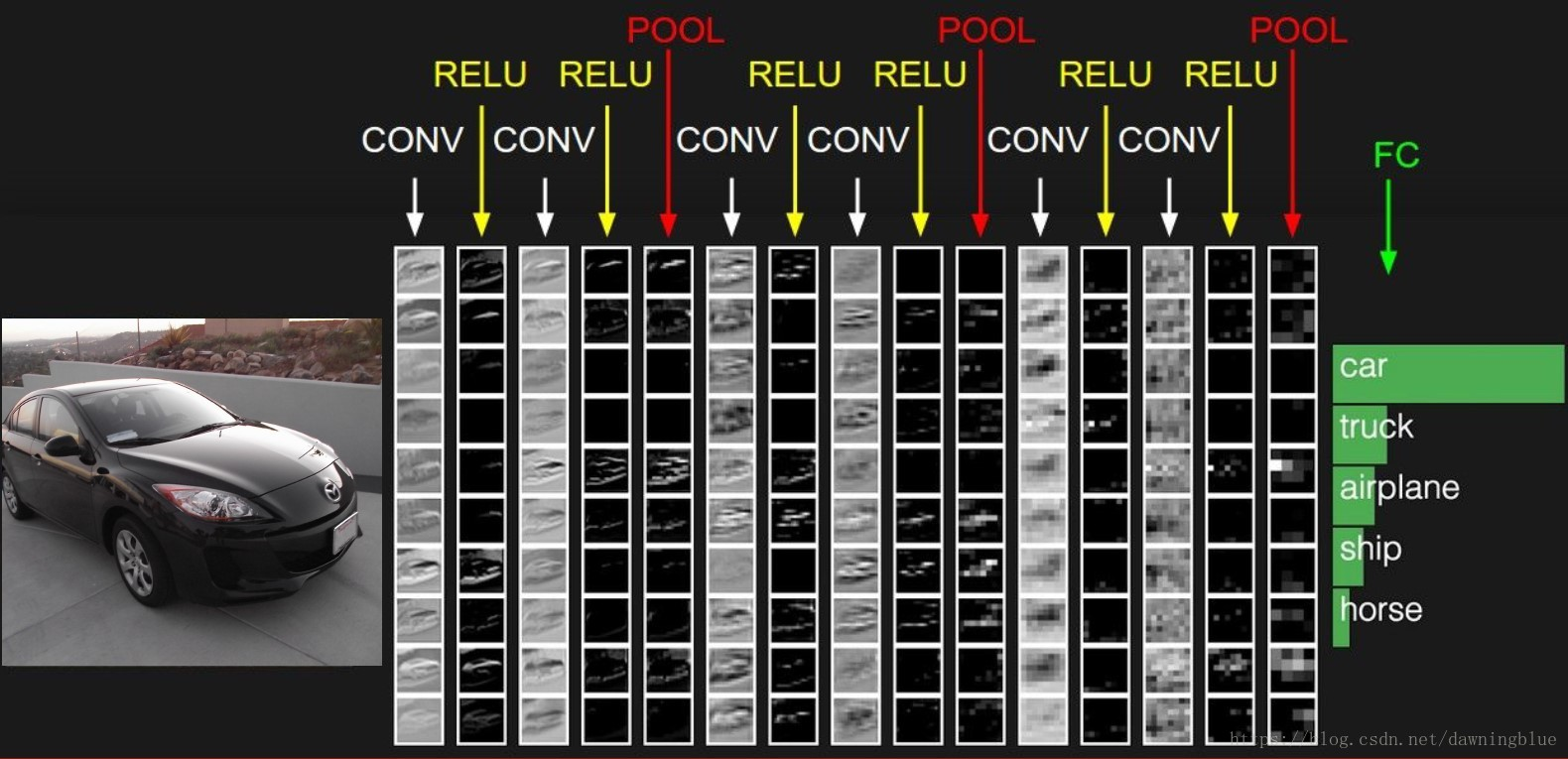
CS231n课程笔记---卷积和池化
原博客:https://blog.csdn.net/dawningblue/article/details/82902336
用不是特别严谨但是比较通俗的语言描述整个过程
卷积神经网络是从卷积层开始介绍的,而卷积层的介绍是从全连接层开始介绍的。
全连接层的处理方式是一次性处理一张图片的全部信息,处理的方式是将图片信息和权重矩阵做乘积,得到一个评分结果。
在细节层面上:
我们会把一张图的全部信息拉成一个一维的向量,一张图的全部信息原始的状态像一个长方体(32x32x3)权重矩阵和这个图片信息的矩阵乘法,本质上来说其实是一次性进行多个点积运算,因为你可以把权重的每一行想象成某一类图像的典型特征,本质上,没有什么矩阵乘法只有点积,或者一次性多个批量的点积,点积才是能说出意义的操作。
最后得到一个评分结果是一个向量,这个向量的纬度和图像的类别数一样,而每一个分量代表这个图片在这个类别上的评分,如果评分越高,那么图片属于这个类别的可能性就越大。于是就有了softmax回归,softmax的本质是在线性回归的基础上,进行了归一化处理,从评分变成了可能性(概率),看起来更直观。
本质上来说,全连接层的提取特征是整体一次性,而卷积层的特征提取是一点一点的提取。
卷积层的处理方法,在最核心的数学处理方面是没有本质不同的,需要借助“点积”这个数学工具,但是整个处理流程上改进了许多。
首先全连接层对图像是整体处理,而卷积是局部多次处理。它背后的深意其实是一开始我们认为图片的特征信息可以一次性就全部提取出来,变为我们认为需要将特征进行分割和组合,经过多次粗到细化才能提取出来的。
具体做法是,我们把之前整个大W变为一个一个小的w, 让每一个小的w和图片上的每一个区域都进行匹配测试(匹配的方式就是用点积),并把匹配的经过进行记录到一个矩阵中去(这些小的权重,通俗而不是专业一点的说法叫做“过滤器(filter), 还有一个更加专业的说法称之为卷积核)之后再拿一个小的w和图片上的每个区域都进行了匹配测试又得到一个矩阵,就这么反反复复(不断训练),得到最优化的权重矩阵。
之后这些矩阵经过激活函数的处理ReLU,处理结果应该还是一个矩阵。
知识点
知识点1:图片是存储信息的形象表达
1. 矩阵表示
典型的灰度图
2. 向量表示
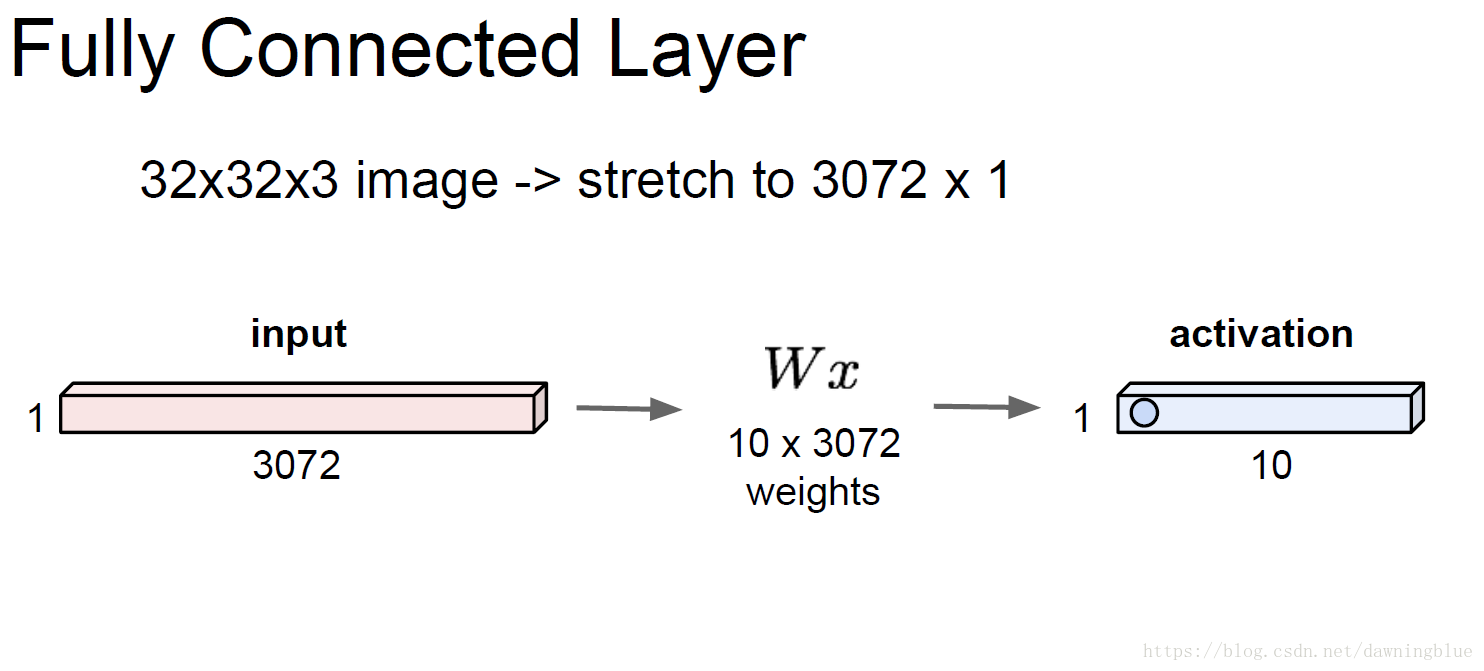
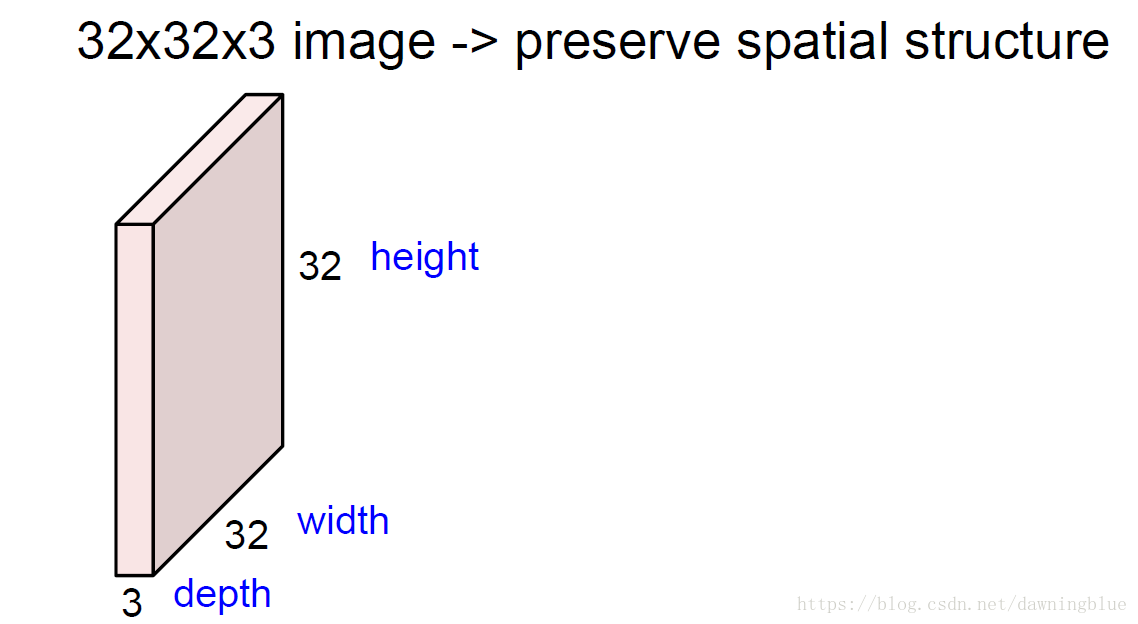
3.长方体表示(volume)
一张RGB图片
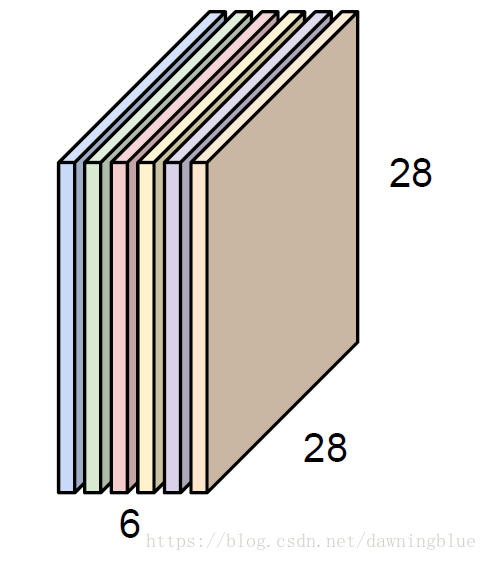
图片的深度具体怎么理解呢?我觉得可以按照RGB三个通道来分成三个平面,可以参考卷积的结果来理解
知识点2:权重

什么叫过滤器,就是符合特征的信息,过滤器能够把它筛选出来,不符合特征的过滤器能把它过滤掉,这个就是过滤器。很明显,这个过滤器其实就是某种图像特征的数学表达式,通过点积运算能够筛选特征匹配度最高的图像部分。
2.2 过滤器的空间特性
过滤器是一个三维的空间矩阵。
我们虽然是用二维的过程来展示,实际上过滤器的数据结构是三维的。
“Filters always extend the full depth of the input volume”
过滤器会延展到输入空间的完整深度。
2.3 运算
过滤器与图像的一部分进行点积运算(其实还要加上一个偏置)得到一个标量数字
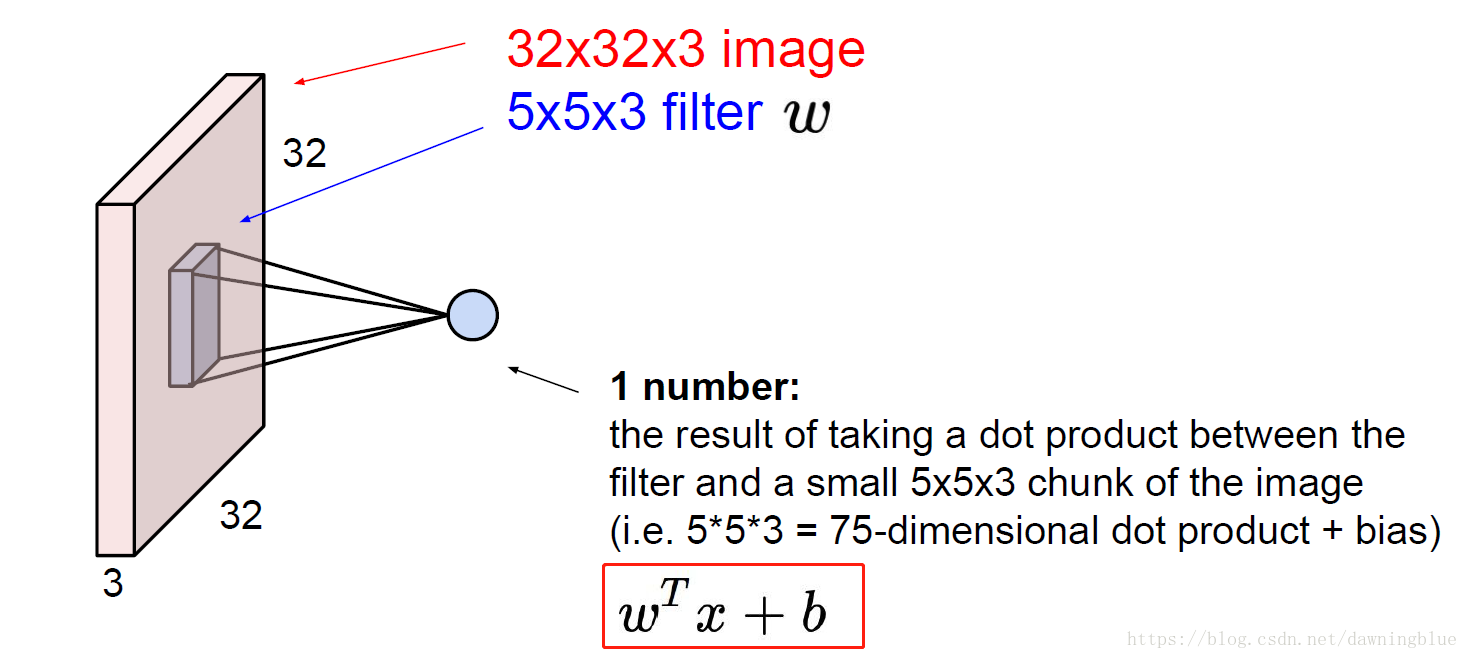
其实就是把以前整张图的权重进行运算的过程变成小权重和图像的一部分进行运算的过程。运算的本质没有变。
2.4 到底是点积还是卷积
我们做的“卷积”, 理论上其运算的方式是,filter和它覆盖的图像,它们在空间位置上一一对应的元素相乘,结果是和把filter以其覆盖的图像分别展成一个一维的向量再做点积结果是一样的。而在计算机实际的实现过程中,我们就是按照展开成一维向量再做点积的方式进行处理的。
那么其实这里的“卷积”和“点积”本质上其实是一样的。
2.5 卷积核里的参数是训练出来的
卷积核就是小一点的权重,而权重都是训练出来的,那么卷积核的权重也是训练出来的。
虽然网络结构是人为设计出来的,但是里面的参数是训练得到的。
2.6 数量关系
从动态特征可以总结出数量之间的关系,有几个常用的表示方法

2.7 感受野
从脑科学神经的角度来理解,卷积核也可以称为“感受野”
2.8 池化层
1. 池化层的作用就是降低数据量
2. 池化层只缩减长度和宽度,不改变深度。
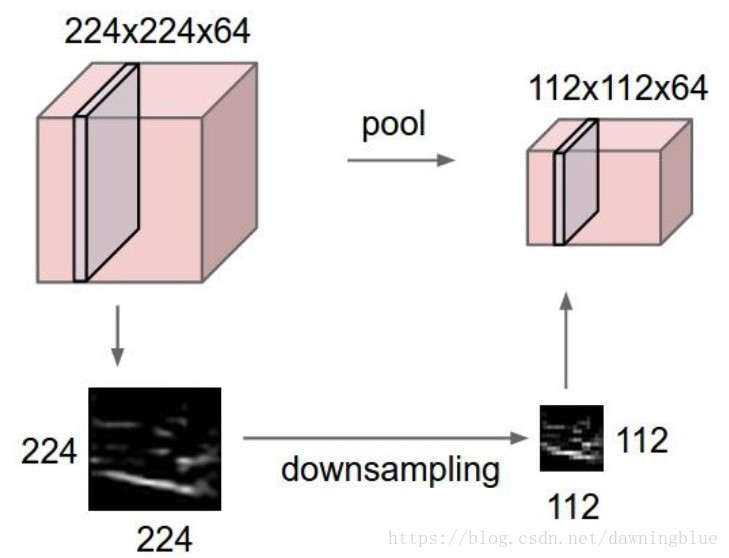
3. 最大池化

从这张图就能看出
3.1 采样的方法其实还是局部扫描的方法(这点和卷积过程一样)
3.2 和卷积不同的地方在于第一,步长采用最高的上限,第二运算的方式是取每个局部的最大值。
4. 为什么是最大池化而不是均值池化
其实每个局部区域中的每一个值都是经过激励函数产生的值,它体现了这个局部的某一特种,我们就拿这个局部特征最明显的那个作为这个局部的代表就可以了。
5. 既然设定步长和池化都能做采样,能否只用步长不用池化或者只用池化而不用步长?
可以这么做,确实在工业界有人这么做。
知识点5: 卷积层重复的次数
LeNet 重复了3次
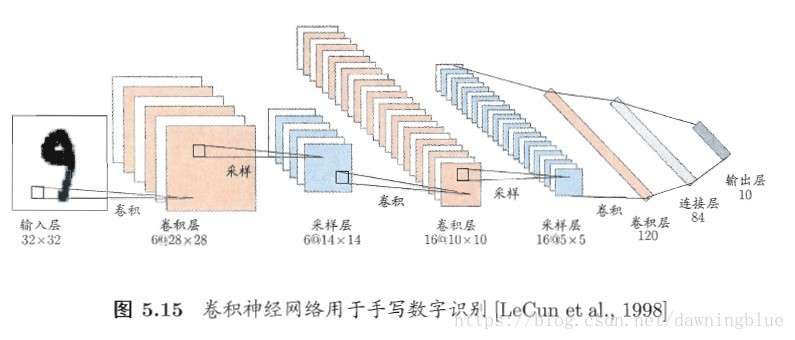
stride例子重复了6次