0412学习笔记 张宇基础30讲——第一讲函数的图像
直角坐标系下的图像:
基本初等函数:常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数
幂函数:
常见考法:求最值——解题思路:找到单调性相同或相反的函数,利用其来求出自身的最值
① 看到pow(u,1/2),pow(u,1/3)都可以用u来求最值,因为在他们共同的定义域上,单调性相同
② 看到 n1*n2*n3可以转化成ln(n1*n2*n3)——ln(n1)+ln(n2)+ln(n3)——ln(ni)的和 再对其进行求导
③ 看到1/u可以用u来求最值,因为在相同定义域上,他们的单调性完全相反
④ 看到 |u| 可以转化成sqrt(u^2),进而求u^2的最值。因为u^2和sqrt(u^2)的单调性相同

指数函数:
注意e^x不存在极限,但存在单侧极限(极限具有唯一性)
对数函数:
① 考研最常出现的考点:x = e^lnx、 u^v = e^(v*lnu)、x^x = e^(x*lnx)
② 求当x趋于0+时,x*lnx的极限:这是未定式,考虑用洛必达法则
比如求当x趋于0+时,x*lnx的极限:x*lnx转化为 lnx / (1/x) ,变成 ∞ / ∞ ,然后使用洛必达法则得到结果为0
七种未定式指路第三章

三角函数:
正弦函数和余弦函数:
① 面积
② 有界性:|sinx|<=1、|cosx|<=1(当x趋于0+时,一般用sinx<=x)
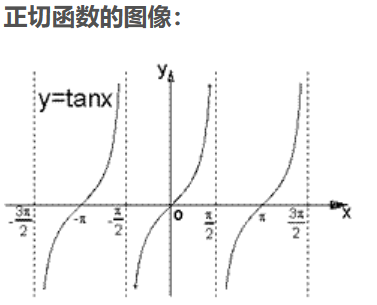
正切函数和余切函数:
tanx cotx
正割函数和余割函数:

反三角函数:
① 反正弦函数(arcsinx)和反余弦函数(arccosx):
arcsinx:定义域:[-1,1],值域:[-π/2,π/2] arccosx:定义域:[-1,1],值域:[0,π]
注意sinx和arcsinx在y∈[-π/2,π/2]是关于y=x对称的,arccosx的图像要自己记住
arcsinx和arccos的导数也需要记住:arcsinx——1/√(1-x²),arccosx—— -1/√1-x²

② 反正切函数(arctanx)和反余切函数(arccotx):
注意tanx和arctanx在y∈[-π/2,π/2]是关于y=x对称的,arccotx的图像要自己记住
arctanx和arccotx的导数也需要记住:arctanx——1/√(1+x²),arccosx—— -1/√1+x²

初等函数:基本初等函数经过有限次四则运算和有限次的复合步骤变成的一个可用一个式子表达的函数
初等函数的定义域可以是一个区间,也可以是一些孤立的点:√( cos(Π*x - 1) )的定义域:x=0、x=±2……
幂指函数 x^x也是初等函数,图像要死记:

画出函数的大致图像:① 求两端 ② 求单调性
分段函数:(非初等函数——用多个式子表达)
① 绝对值函数( y = | x | )
② 符号函数(y = sgn x [ x>0:1;x=0:0;x<0:-1 ] )
③ 取整函数( y = [ x ] :x->0+:lim [ x ] = 0、x->0-:lim [ x ] = -1 ):一般求极限用到夹逼准则:x-1 < [ x ] <= x
图形变换:
① 平移变换:f ( x + x0 ) —— 图像 f ( x )向左平移 x0、f ( x - x0 ) —— 图像 f ( x )向右平移 x0、f ( x ) + y0 —— 图像 f ( x )向上平移 y0、f ( x ) - y0 —— 图像 f ( x )向下平移 y0
② 对称变换:
关于x轴对称:y = f ( x ) -> y = - f ( x )
关于y轴对称:y = f ( x ) -> y = f ( -x )
关于原点对称:y = - f ( -x )
关于 y = x对称:y = 1 / f ( x )
f ( x ) 取值全部为正:y = | f ( x ) |
x轴右边图像消失,被左边图像取代:y = f ( | x | )
③ 伸缩变换
水平伸缩:y = f ( kx ) —— 横坐标变为原来的1/k,纵坐标不变
垂直伸缩:y = k * f ( x ) —— 横坐标不变,纵坐标变成原来的k倍
极坐标系下的图像:( g ( r , θ) = 0 )
① 描点法画图像(土办法,根据一个个点画出图)
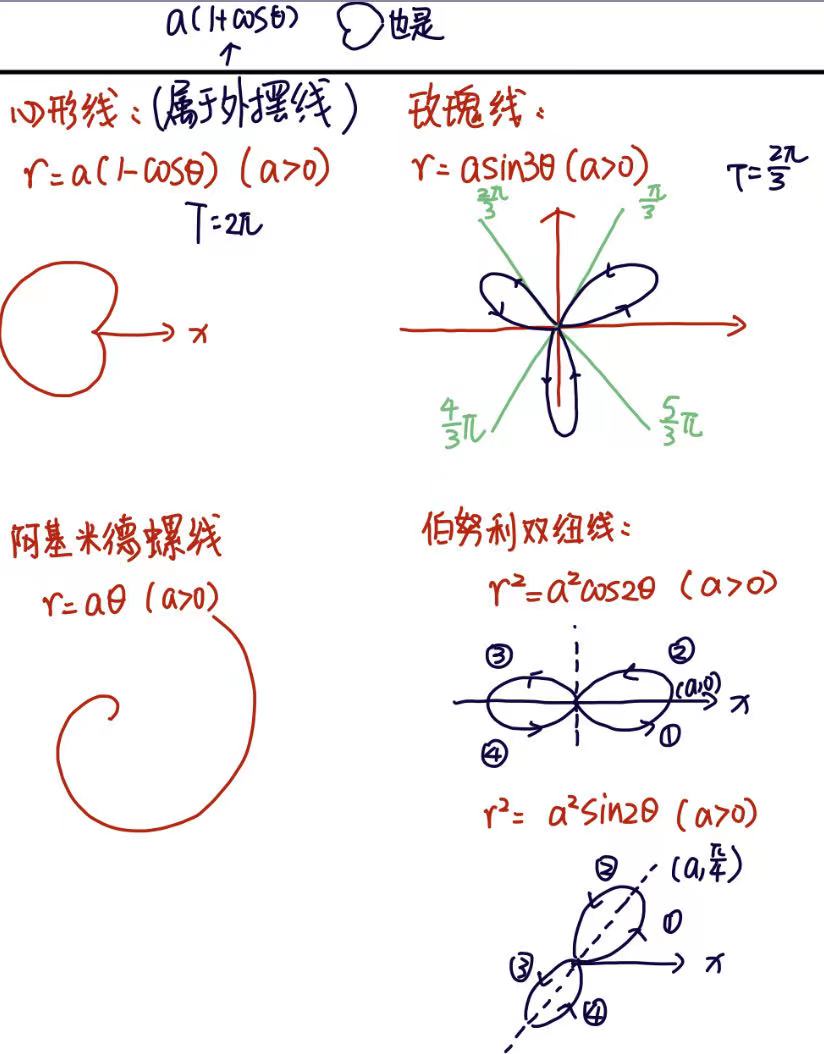
② 直角坐标系观点画极坐标系下的图像(直角坐标转极坐标,极坐标转直角坐标,f ( x , y ) = 0 )
我的理解:就是把极坐标中的r转变成y画在xy直角坐标系下,例如心型线在θ=0时,r=0,则y=0

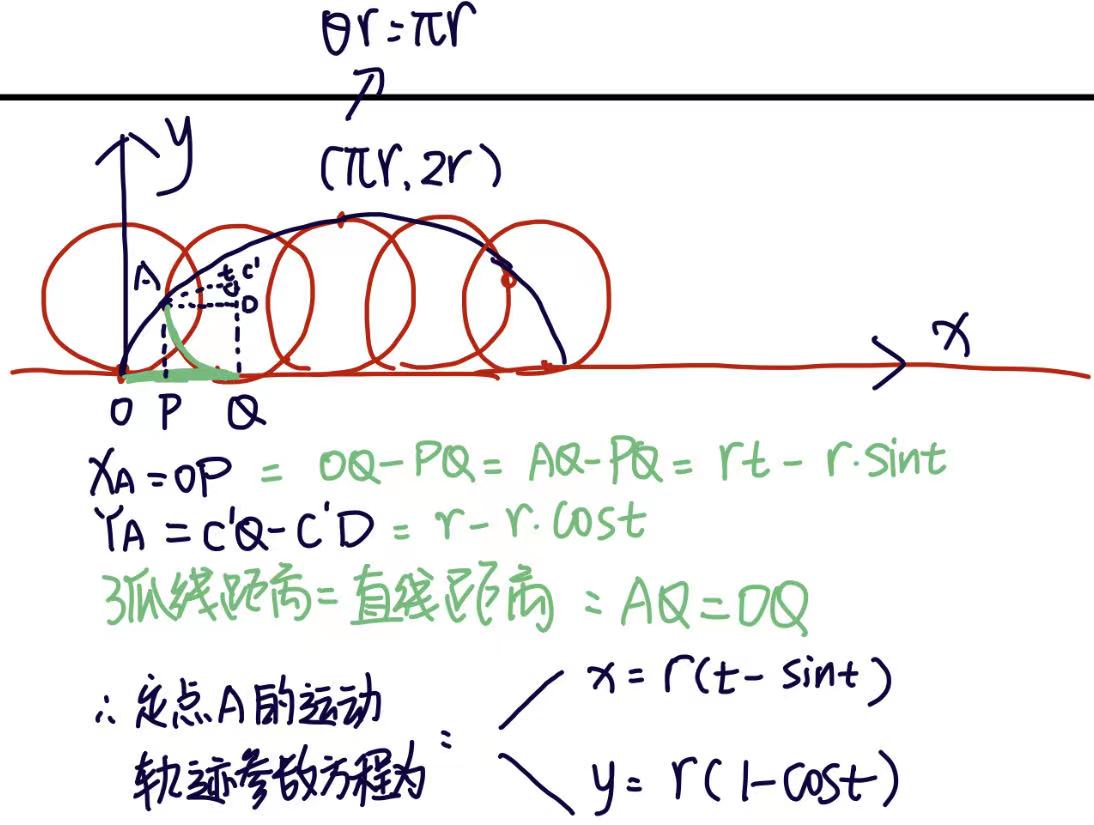
③ 参数法(x = x ( t )、y = y ( t ) )
ps:有些曲线很难用极坐标和直角坐标表达(x , y间函数表达式比较复杂),则用参数法表示曲线方程
① 摆线(平摆线)
② 星型线(内摆线——一个小圆在一个固定的大圆内做纯滚动)
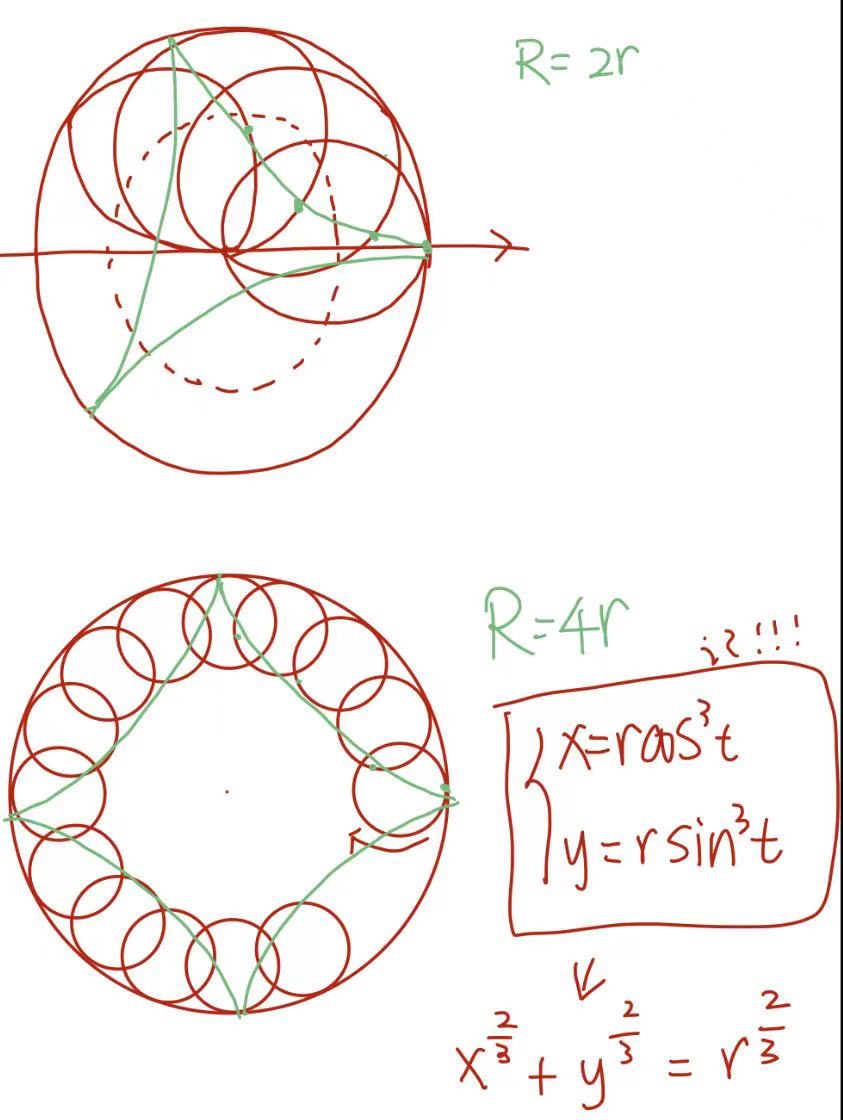
常用基础知识:
数列:
等差数列:求和:Sn = (a1 + a1 + (n-1)*d )* n / 2
等比数列:求和:有限项:Sn = ( a1*(1-q^n) ) / 1-q 无限项:常用1 + q + q^2 + q^3 +…… + q^n = (1 - q^n) / 1 - q
常见的数列前n项和:
① Σk = 1+2+3+……+n = (1+n)*n/2
② Σk^2 = 1^2+2^2+3^2+……+n^2 = n(n+1)(2n+1)/6
③ Σ1/k*(k+1) = 1/1*2 + 1/2*3 + …… + 1/n*(n+1) = 1-1/(n+1) = n/n+1
三角函数:
csc x = 1/sinx sec x = 1/cosx cot x = 1/tanx = cosx/sinx
诱导公式:奇变偶(n*Π/2为奇,n*Π为偶数)不变,符号(加减一个数之后看属于原函数的哪个区域。比如sin(2/Π+α),2/Π属于奇,(2/Π+α)在sinx图像的第二象限,按照sinx的值域来看,仍为正,所以sin(2/Π+α) = cos(α))看象限
倍角公式:
sin(2α) = 2sinαcosα
coa(2α) = cos^2 - sin^2 = 2cos^2 - 1
tan(2α) = 2tanα / 1-tan^2 α
cot(2α) = cot^2 α - 1 / 2*cot α
半角公式:
sin^2 ( α/2 ) = 1/2 * (1 - cosα)
cos^2 ( α/2 )= 1/2 * (1+cosα)
tan ( α/2 ) = sinα / 1+cosα
cot ( α/2 ) = 1+cosα / sinα
和差公式:
sin(α±β) = sinαcosβ + cosαsinβ
cos(α±β) = cosαcosβ ∓ sinαsinβ
tan(α±β) = tanα ± tanβ / 1 ∓ tanαtanβ
cot(α±β) = cotαcotβ ∓ 1 / cotβ±cotα


指数运算法则:
a^a * a^b = a^(a+b)、 a^a / a^b = a^(a-b)、 (a^a)^b = a^ab、 (ab)^a = a^a * b^a、 (a/b)^a = a^a / b^a
对数运算法则:
loga MN = logaM + logaN
logaM/N = logaM - logaN
logaM^n = nlogaM
logaM^1/n = 1/n *logaM
一元二次方程基础:
一元二次方程:ax^2 + bx +c = 0
求根公式:-b±√b^2-4ac / 2a
韦达定理(根与系数的关系):x1+x2 = -b/a,x1x2 = c/a
判别式:Δ = b^2 - 4ac Δ>0:有两个不同的根 Δ = 0:有两个相同的根 Δ<0:有两个共轭复根:-b ± (√4ac-b^2) i /2a
抛物线顶点:(-b/2a , 4ac - b^2 / 4a)
因式分解公式:
重点要记住:
a^3 + b^3 = (a+b)(a^2-ab+b^2)
a^3 - b^3 = (a-b)(a^2+ab+b^2)
n是正整数:a^n - b^n = (a - b)*(a^n-1 + a^n-2 * b + a^n-3 * b^2 + …… + b^n-1)
n是正奇数:a^n + b^n = (a + b)*(a^n - 1 - a^n-2 * b -……- a*b^n-2 + b^n-1)
二项式定理:
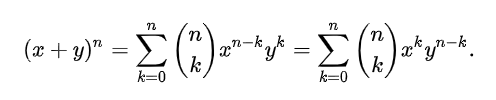
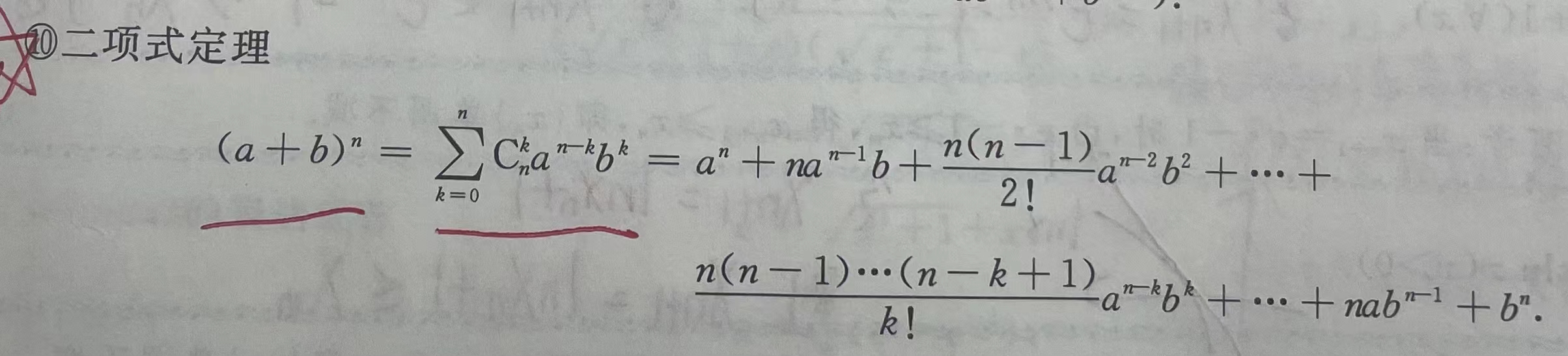
阶乘与双阶乘:
n! = 1*2*……*n(注意:0! = 1)
( 2n! ) = 2*4*6*8*……*2n = 2^n * n!
( 2n-1! ) = 1*3*5*……*2n-1
点火公式:
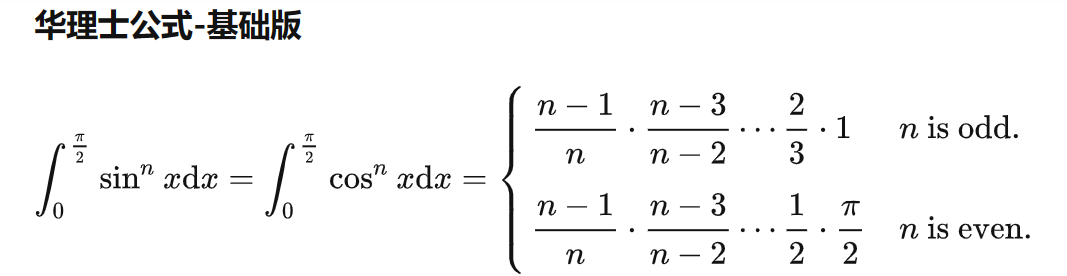

常用的不等式:(可以用于证明函数有界、找到Xn+1和Xn的关系:是递增还是递减、判断数列的单调性)
① | a+b | <= | a | + | b |
② | | a | - | b | |<= | a-b |
③ √ab <= (a+b) / 2 <= √(a^2 + b^2) / 2 ————> | ab | <= (a^2 + b^2) / 2( 算数平均<=几何平均<=均方根 )
④ 3√abc <= (a+b+c)/3 <= 3√(a^2 + b^2 + c^2)
⑤ 若0<a<x<b,0<c<y<d,则 c/b < y/x < d/b(注意字母,越小的数要除越大的数)
⑥ sinx < x < tanx(0<x<Π/2)
⑦ sinx < x(x>0)
⑧ arctanx <= x <= arcsinx(0<=x<=1)(记住图像)
⑨ e^x >= x+1(任意x)
⑩ x-1 >= lnx(x>0)(很简单,自行画图)
⑩ 1/(x+1) < ln(1+1/x) < 1/x(x>0)证明:ln(1+1/x) = ln(x+1) - lnx 若存在一个点ε∈[x,x+1],则在此区间上使用拉格朗日中值定理:ln(x+1) - lnx = f'(ε)*(x+1-x) = 1/ε
又因为x>0,x+1>ε,x<ε,x+1>x,所以ε>0,且1/(x+1) < 1/ε < 1/x
一定会考的图像!!!!!!:
反双曲正弦函数:√ln(x+√(x^2+1))
导数:1/√(x^2 + 1)
双曲正弦函数:(e^x - e^-x)/2

注意:上面两个函数都是奇函数,如果题目让求微分,则奇函数在对称区间内为0
双曲余弦函数:(e^x+e^-x)/2——偶函数
回忆考点:F(X) = f(x)-f(-x)必为奇函数,F(X) = f(x)+f(-x)必为偶函数


