Macro / Micro / Weighted AUC 如何计算实例讲解
情景:二分类模型在验证集上的 outputs 为 [[-0.0464, -0.0268], [-0.0234, -0.0091]],验证集 labels 为 [0, 1]。一步一步推导出 AUC。
- 首先明确几个概念
-
TPR: sensitive/recall,检测出来的阳性样本的占比,适用于癌症筛查
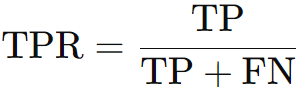
-
FPR:模型是否把所有的阴性样本都预测成了阳性
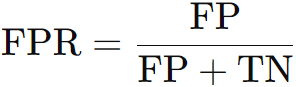
👉极限情况1:TPR = 1 & FPR = 1,说明模型把所有样本都预测成了阳性(包含两个含义:对于阳性样本,模型都能检出;但对于阴性样本,模型都判断错误)。但显然,这种情况下,那些未患病的被试(阴性样本)会经历没必要的检查,所以不应该鼓励模型把所有样本都预测成阳性。
👉极限情况2:TPR = 0 & FPR = 0,说明模型把所有样本都预测成了阴性(同样包含两个含义:没有无辜的被试受模型所害,但真正患病的被试也被模型漏掉了)。这样一来,模型也失去了诊断价值,白白浪费被试们的时间。实际临床应用中,应该根据实际需求选择偏重提高TPR还是降低FPR。 -
AUC 值为 ROC 曲线下面积:ROC 曲线图的横坐标为 FPR,纵坐标为 TPR,根据不同阈值下的 [FPR, TPR] 点对 ROC 曲线进行绘制。结合上面的两种极限情况,ideal的 ROC 曲线会先后经过(0, 0)、(0, 1)、(1, 1)三个点,代表对于所有的阈值,FPR 都等于0,同时 TPR 都等于1。在实际情况中,越接近于左上角的 ROC 曲线越理想。
- 计算AUC
-
将outputs通过Softmax先转换成概率分布(参考我们的另一篇文章),得到 [[0.4955, 0.5045], [0.4977, 0.5023]]。
-
将 outputs 看成 one-hot 格式,得到预测样本为正类(1)对应的的概率是:[0.5045, 0.5023]。
-
将 [0.5045, 0.5023] 作为两个阈值,讨论当阈值分别为 ∞、0.5045 和 0.5023 时,正负样本的预测情况。
-
阈值的作用
在二分类问题中,模型输出的分数通常表示样本属于正类的概率或相关性。我们可以通过设置不同的阈值来决定样本是被预测为正类还是负类:如果预测分数高于/等于阈值(sklearn.metrics.roc_curve),我们将样本分类为正类;如果预测分数低于阈值,我们将样本分类为负类。 -
具体过程如下
1> 阈值为 ∞ 时,两个样本均为负类。
2> 阈值为 0.5045 时,第一个样本:分数为 0.5045,等于阈值,所以预测为正类;第二个样本:分数为 0.5023,低于阈值,所以预测为负类。
3> 阈值为 0.5023 时,第一个样本:分数为 0.5045,高于阈值,所以预测为正类;第二个样本:分数为 0.5023,等于阈值,所以预测为正类。
-
-
计算不同阈值下的 TPR、FPR 分别是多少(真实标签为 [0, 1])
1> 阈值为 ∞ 时,预测标签为 [0, 0],TPR=0,FPR=0。
2> 阈值为 0.5045 时,预测标签为 [1, 0],TPR=0,FPR=1。
2> 阈值为 0.5023 时,预测标签为 [1, 1],TPR=1,FPR=1。 -
根据上面的三个点绘制 ROC 曲线(横坐标:FPR,纵坐标:TPR),根据阈值从大到小,三个点分别为(0, 0)、(1, 0)、(1, 1)。
-
绘制出的 ROC 曲线的曲线下面积为 0, 所以 AUC=0。
⭐只有在多分类问题下面,讨论 macro / micro / weighted AUC 的区别才有意义。因为如果是二分类问题,只会有一组正类和负类、一条ROC曲线。计算普通的 average/macro AUC 即可。多分类问题下,每个正类都画一条 ROC 曲线,然后选择不同的方法(macro / micro / weighted),得到最终多分类的 ROC 曲线,从而计算 AUC。


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步