javascript 算法 ---递归

“要理解递归，首先要理解递归。” ——佚名

递归函数是在函数内部能够直接或间接调用自身的方法或函数。

假设一个函数一直调用自己结果是什么？单就上述情况而言，它会一直执 行下去。因此，每个递归函数都必须有基线条件，即一个不再递归调用的条件（停止点），以防 止无限递归。 

function A(X) {   
　　const recursionAnswer = confirm('Do you understand recursion?');
   if (recursionAnswer === true) { 
　　　　//基线条件 ，停止点
   　　 return true; 
  　}  
　　//递归调用
 　　A(recursionAnswer); 
 } 

作为递归的第一个例子，我们来看看如何计算一个数的阶乘。数 n的阶乘，定义为 n!，表示 从 1到 n的整数的乘积。
5的阶乘表示为 5!，和 5 × 4 × 3 × 2 × 1相等，结果是 120。（注意一个概念定义 0！= 1，不是等于 0）

 function factorial(x){
    //基线
    if(x == 0 || x==1){
       return 1;  
    }
    //递归调用
    
    return    x*factorial(x-1);

}

斐波那契数列

 0、1、1、2、3、5、8、13、21、 34等数组成的序列。数 2由 1 + 1得到，数 3由 1 + 2得到，数 5由 2 + 3得到，以此类推。斐波 那契数列的定义如下。 

 

 

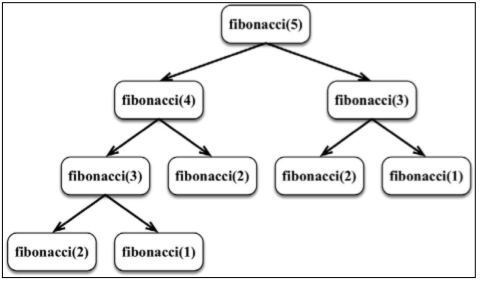
//迭代的方法

function fibonacciIterative(n) {  
       if (n < 1) return 0;
       if (n <= 2) return 1; 
       let fibNMinus2 = 0;  
       let fibNMinus1 = 1;  
       let fibN = n;  
       for (let i = 2; i <= n; i++) { 
             // n >= 2 
            fibN = fibNMinus1 + fibNMinus2; 
            // f(n-1) + f(n-2)   
            fibNMinus2 = fibNMinus1;  
            fibNMinus1 = fibN;  
       }   
  return fibN; 
} 
                       

//递归的方法

function fibona(n){
    if(n <= 2)
    {
        return 1;
    }
    if(n < 1)
    {
        return 0;
    }
    reurn fibona(n-1)+fibona(n-2);
}