神经网络

 

1. 神经网络模型开发动机

神经网络可以解决非常复杂的非线性分类问题。当特征数量特别多时， 可以考虑使用该算法。

 

解释一下非线性

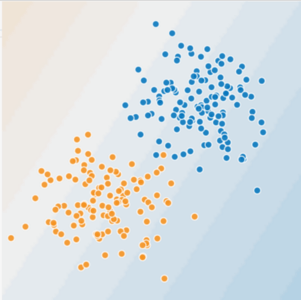图中， 蓝色表示生病的树， 橙色表示健康的树。 如果使用一条直线， 则可以区分开来，做出很好的预测。

 

但是如果是以下这种

如果是这种情况， 使用直线无法区分，这就是非线性问题。

需要使用两个或者多个特征相乘来对特征空间中的非线性规律进行编码的合成特征， 即叫特征组合。

如果有两个特征x1, x2, 则添加新的特征 x3 = x1 * x2

最后线性公式变成

 

 

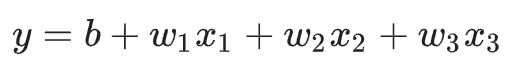现在假设有如下一个分类

如果需要一个算法，来对该图中进行区分，则神经网络是比较好的解决方案。

 

比如判断照片中是否有小汽车时。

 

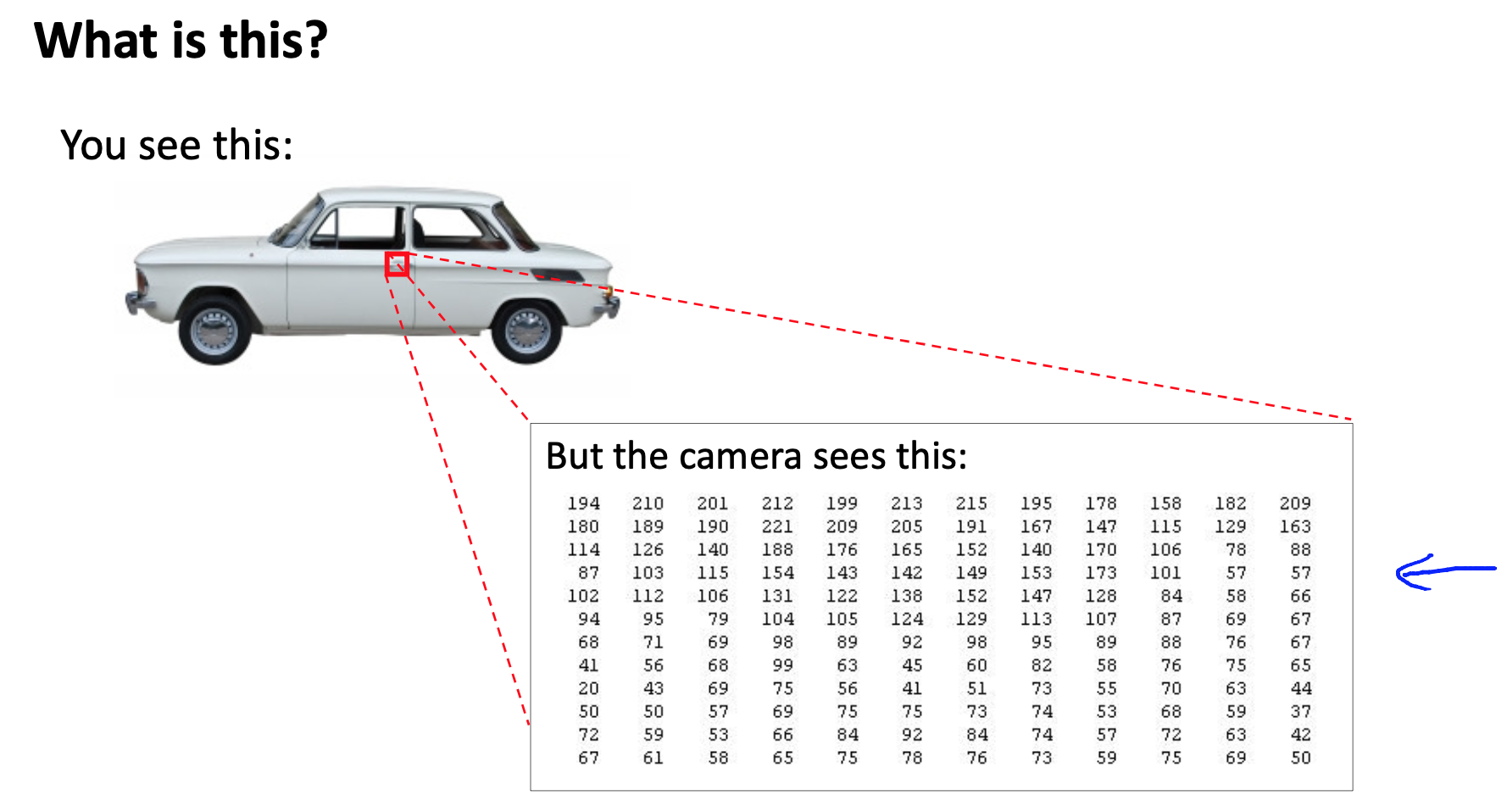如上所示， 人们通过肉眼，可以很容易的分辨出图片中显示的是一个小汽车。但是计算机通过摄像机获取到的是一个矩阵

其中每个像素的值是一个RGB颜色， 值的范围在0-255。

如果是一张50 * 50 像素的图像， 则会有 50 * 50 = 2500个像素单位

如果是彩色，每个像素又有0-255的RGB取值。即有 50 * 50 * 3 = 7500

特征数量则有约 n^2 / 2  约 3000000 个特征数量。

 

 

2. 神经网络表示

下面这张是最简单的神经网络架构，只有输入层与输出层

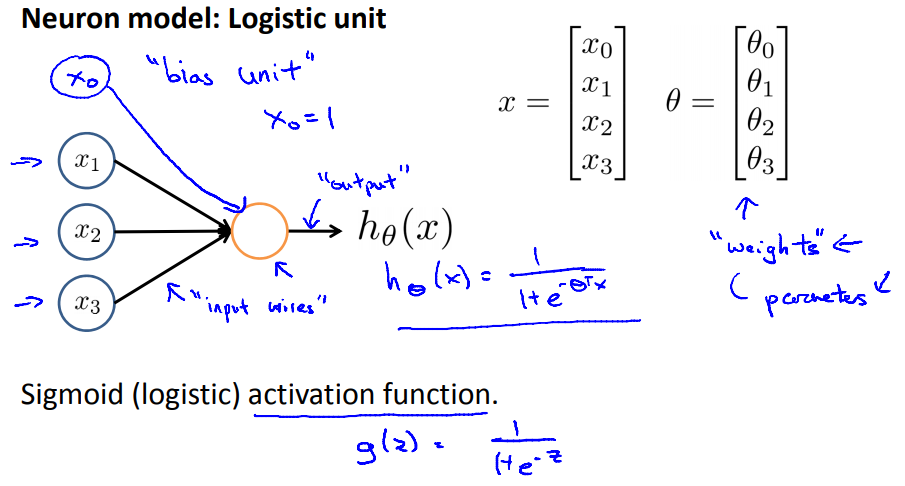该函数使用逻辑激活函数， 中间黄色的圈就是神经网络单元， 神经网络就是由这个神经单元组成的。

其中有一些最基本的组件：

* 一组节点，表示神经单元

* 一组权重， theta， 表示节点的权重

* 输入层数据

* 激活函数

 

下面这张是有一个中间层的神经网络

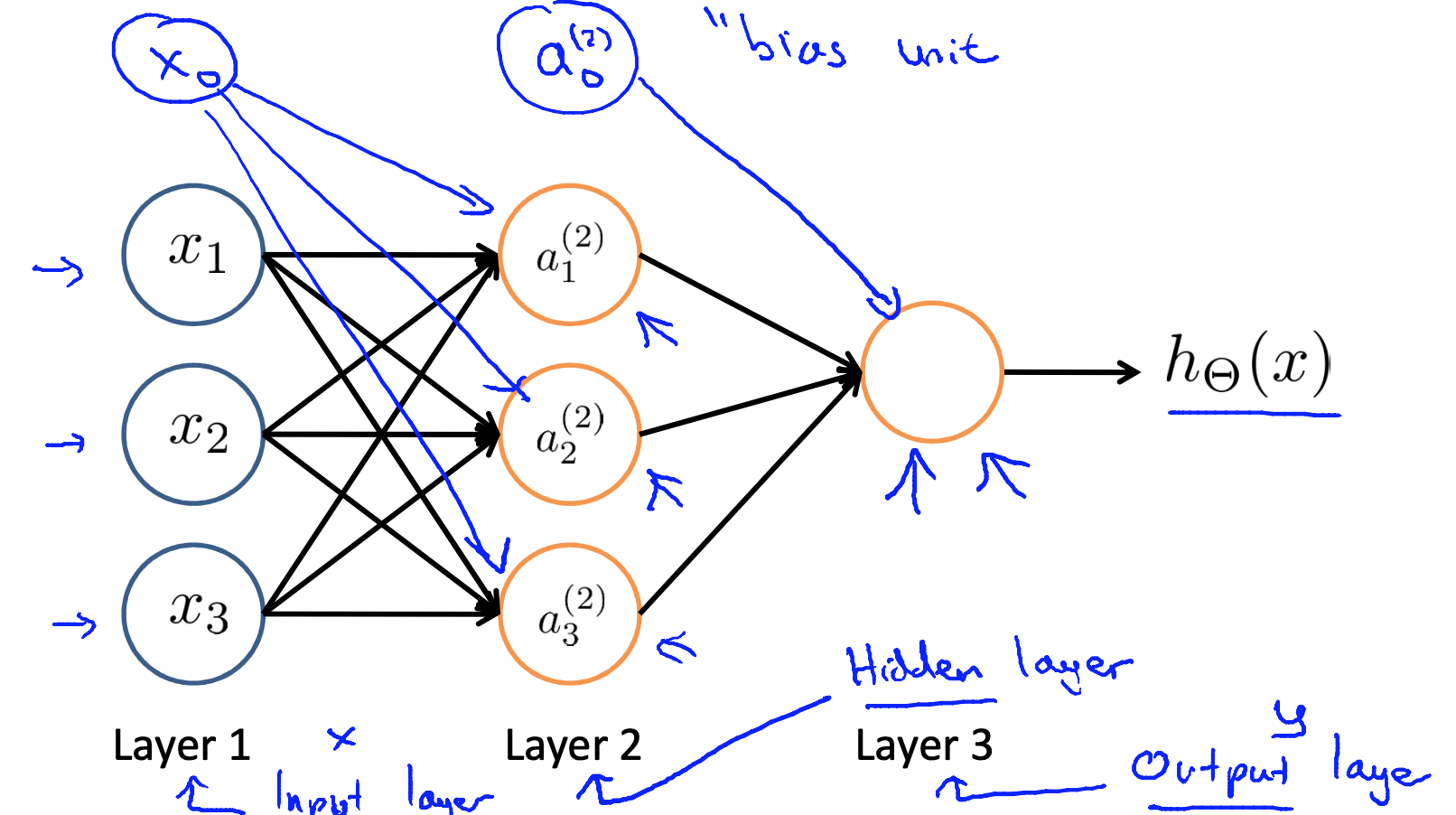神经网络是由层组成的， 第一层叫输入层， 中间层叫隐藏层，最后一层叫输出层。

 

下面仔细仔细分析上面这个神经网络的计算过程

定义一些术语

a_i^(j) 用来表示神经网络隐藏层的单元，也称激活单元， i 表示第几个神经元， j 表示第几层。

大写的theta表示一个矩阵， 表示上一层与下一层之间的关联，即是其中的weight值。

其中输入层j = 1 , 有s_j = 3个神经单元， 中间层 j = 2 有 S_j+1 = 3个神经单元, 大写theta 是一个 3 * 4 维的矩阵。

 

中间层，则有如下表示， 上标(2) 表示第2层， 下标表示第几个神经单元。

 

每个神经单元的激活函数

g() 表示S型函数，或者使用的激活函数，即逻辑回归函数

 

 

对上式进行向量化变换操作

 

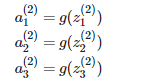对于第2层, j = 2 , 与节点 k ， 变量 z 有如下表示

 

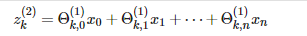向量表示如下

 

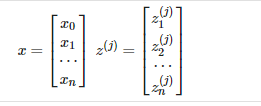即z^(j) 有如下表示

 

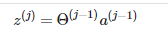最后h(theta)(x)

 

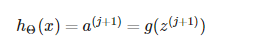整个过程叫做前向传播。

 

 

 

案例1：有如下神经网络， 其中x0 = 1

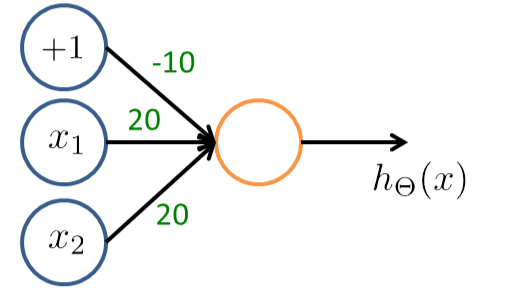并且 权重值已经 算出

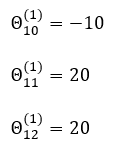整式等于

如果有如下图

则该神经网络处理如下

x1	x2	h(theta)X
0	0	0
0	1	1
1	0	1
1	1	1

所以执行与操作

 

 

 

案例2： 使用中间层来计算XNOR运算

 

 

 

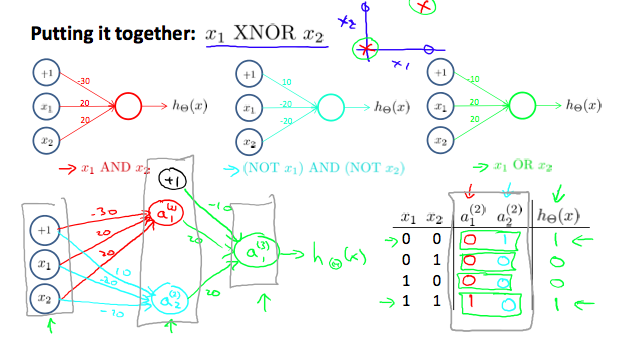一对多的分类

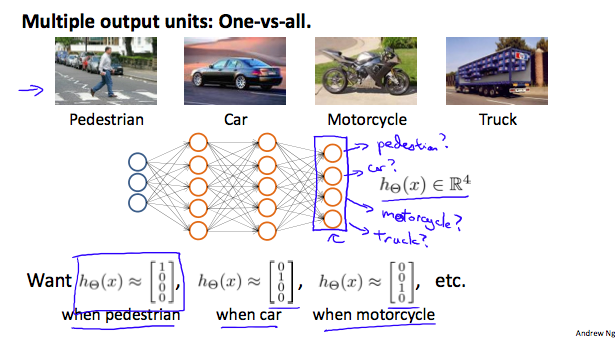输入是一张照片，输出结果是一个向量。

 

 

 

2. 成本函数(Cost Function)

假定神经网络架构如下

 

变量定义

L 表示网络中有多少层，如上架构中， L = 4

S_l 表示第l层有第几个神经单元，比如 l = 4 , S_l = 4

k 表示输出层有几个神经单元， k = 4

 

对于逻辑回归中的成本函数有哪下定义

 

则神经网络成本函数如下

 

 

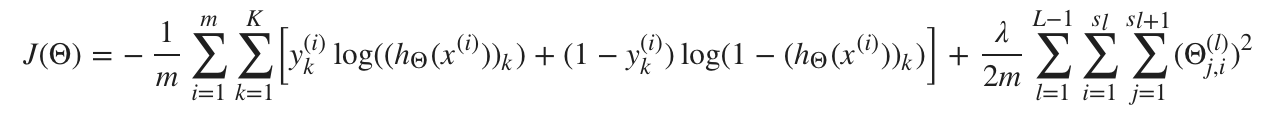3. 反向传播算法（Backpropagation Algorithm）

使用把向传播算法来min(J_theta)