逻辑回归
1. 逻辑回归
多元线性回归是用线性的关系来拟合一个事情的发生规律,找到这个规律的表达公式,将得到的数据带入公式以用来实现预测的目的,
习惯将这类预测未来的问题称作回归问题。 机器学习中按照目的不同可以分为两大类:回归和分类.
逻辑回归就可以用来完成分类任务.
1.1 二元分类实现方式
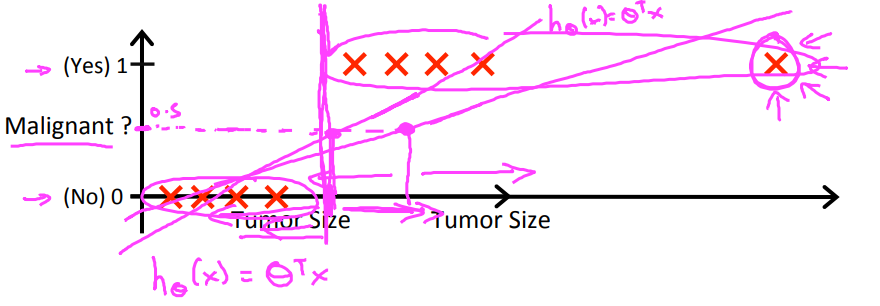
如果只有两种可能, 是(1) 或者 不是(0), 可以使用线性回归来拟合数据,然后设定一个阀值
 |
如果y的结果 大于该值, 则输出为1
如果y的结果 小于该值, 则输出为0
但是如果将Tumor Size的数据值拉长, 则会导致拟合的线太直, 数据的离群值太大。
所以该分类问题如果使用该思想,有两个问题需要解决
第一, 拟合的是一条直线,如果有异常值,导致线太直,离群值过大。
第二, 如何确定阀值。
1.2 假设函数
假设函数定义如下
 |
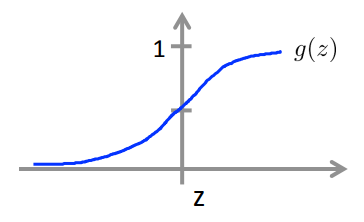
这个函数叫做Sigmod函数, 或者逻辑方程。
sigmod 函数使用octave 实现
function g = sigmoid(z) %SIGMOID Compute sigmoid function % g = SIGMOID(z) computes the sigmoid of z. % You need to return the following variables correctly g = zeros(size(z)); % ====================== YOUR CODE HERE ====================== % Instructions: Compute the sigmoid of each value of z (z can be a matrix, % vector or scalar). g = 1 ./ (1+exp(-z)); % ============================================================= end
分别使用如下值进行测试
octave:16> sigmoid(100)
ans = 1
octave:17> sigmoid(-100) ans = 3.7201e-44 octave:18> sigmoid(0) ans = 0.50000
该函数的输出值使用图表表示如下
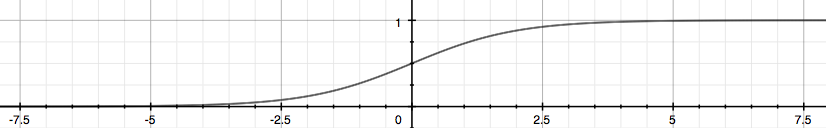 |
可以看出,此时,0 <= h(theta)(x) <= 1
1.3 决策边界
sigmod 公式如下
 |
根据sigmod函数性质, 可以有如下结论
 |
如果 g(z) >= 0 , 则对于二元分类,预测输出值为1
如果g(z) < 0, 预测输出值为0
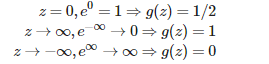 |
第一个例子
 |
第二个例子, 非线性
 |
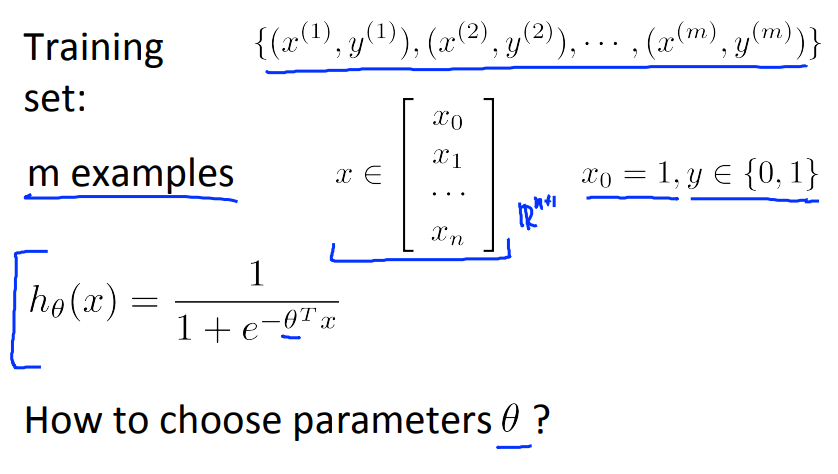
1.4 损失函数
问题如下
 |
损失函数如下
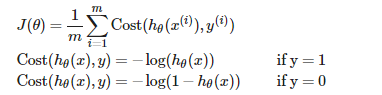 |
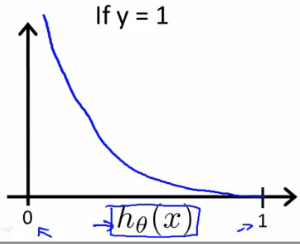
当y = 1 时, J(theta) 与 h(theta)(x) 之间关系如下图
|
当y=0时, 关系如下
 |
有如下的函数性质
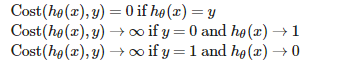 |
其中损失函数可以写成下面的形式
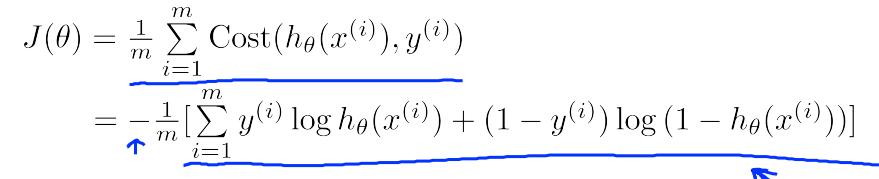 |
向量形式
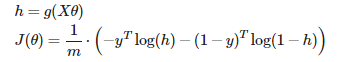 |
现在目标是要最小化 J(theta)
1.5 梯度下降
 |
继续变换形式
 |
与线性回归算法一样。
向量化形式
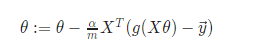 |
算法优化
共轭梯度法(Conjugate Gradient)
BFGS
L-BFGS
1.6 一对多的分类
当输出结果不是0,1两个, 而是由多个组成的
有如下方程
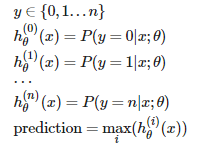
|
选择概率最大的那个值。
2. 过度拟合(Overfitting)
欠拟合(underfitting), 是表示学习的样本特征太少, 无法很好的满足数据。
过度拟合(overfitting), 表示特征太多,导致无法很好预测新的数据。
解决方案:
1. 减少特征值
- 手动选择需要保留哪些特征值
- 使用模型选择算法自动选取
2. 规则化
- 保留所有特征
正则化思想如下
 |
函数表达式如下
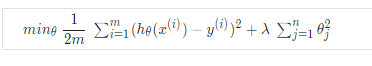 |
lambda 是一个规则化参数
如果lambda 太大, 可能会导致欠拟合
规则化线性回归的梯度下降算法
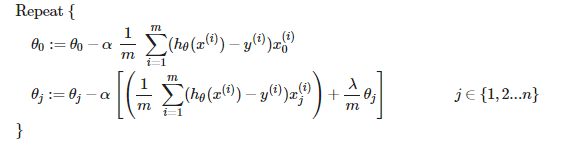 |
该式进行变换后, 表示如下
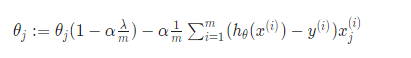 |
规则化线性回归正规方程解
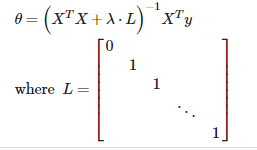 |
规则化逻辑回归的梯度下降算法
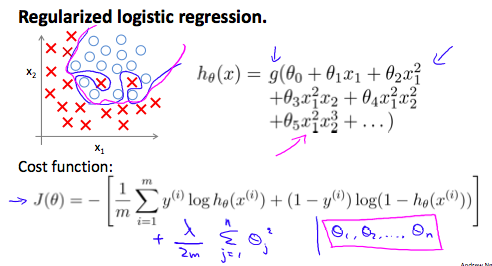 |
逻辑回归规则化方程
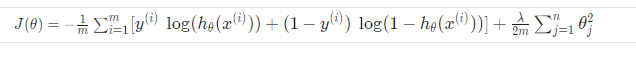 |
梯度下降
 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号