线性回归

 

1. 线性回归

回归是常用的一种数据分析的方法，通过规定因变量和自变量来确定变量之间的因果关系，建立一种回归模型，并根据实测数据来求解模型的各个参数，

然后评价回归模型是否能够很好的拟合实测数据，回归分析，可以帮助我们对数据做出合理的预测，其一般使用流程如下：

 

 

 

1.1 单个输入变量

假设我们有一组数据

序号	1	2	3	4	5	6	7	8	9	10
x(平方)	30	40	50	60	70	80	90	100	110	120
y(万)	40	60	65	80	90	100	120	130	145	150

其中x 表示房子的面积， y 表示出售的价格。 现在我有一个150平的房子， 我想知道大概的价格是多少？

 

第一步，将问题抽象化

输入参数只有一个， 房子的面积， 输出参数也只有一个，房子的价格， 一共有10条数据，设为 m = 10, 每一条数据使用 i 来标号。

则每条数据表示为

 

 

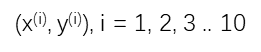定义如下机器学习算法, x 表示输入面积，y 表示输出结果

 

 

 

 

表示 H(Hypothesis)

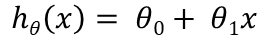本式中， theta0, 与 theta1 是参数， x 表示输入的面积

想法： 选择合适的参数，使得结果非常接近我们的结果值

 

第二步：损失函数

确定theta 0  与 theta 1 的参数值，可以拟合我们的模型数据。

 

 

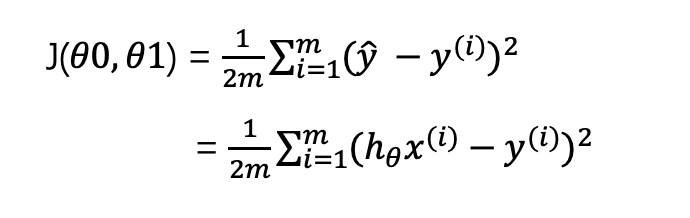
求出所有点到该直线的距离，并且值是最小值。

这个函数也叫做一元线性回归方程的均方误差函数(Squared Error Function)

 

 

第三步：计算 minize(theta1, theta2) = J(theta1, theta2)

假设theta0 是0，只有一个参数 theta1

 

假设theta1 为0 ， 则求 minize(theata1, theta2) = minize(theta2)

 

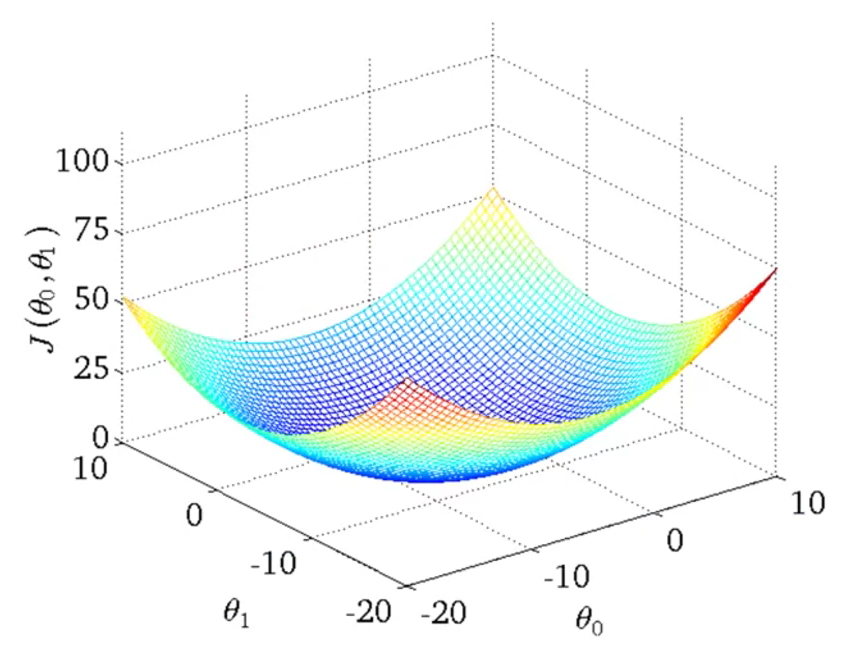
对于2个参数的变量，J(theta1, theta2) 最终的所有结果图形如下

 

 

 

 

 

1.2 多个输入变量

序号	1	2	3	4	5	6	7	8	9	10
x1(平方)	30	40	50	60	70	80	90	100	110	120
x2卧室数量	1	1	1	2	2	3	3	3	4	3
x3房龄	3	5	4	4	6	7	3	2	5	4
y(万)	40	60	65	80	90	100	120	130	145	150

其中x 1表示房子的面积，

X2表示房屋数量

X3表示房子年龄

 

y 表示出售的价格。

现在我有一个150平的房子，有四个卧室，房子年限是5年，我想知道大概的价格是多少？

 

对数据进行定义，抽象化

用m表示有多少个训练集 ，m = 10

用 n 来表示有多少个特征， 此例中n = 3

x^{(i) 来表示是第几个数据集， i 表示序列号}

x_j⁽ⁱ⁾ 来表示第几个数据集中第几个特征

 

此时假设函数为

根据此式扩展， 有n个特征，则线性回归假设函数形式为

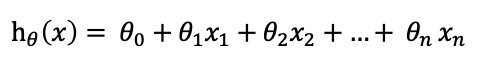为了便于记忆，可以定义x0 = 1, 则有如下定义

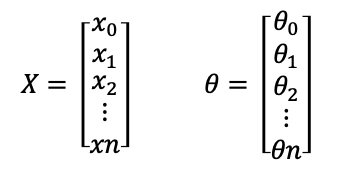则原式h_theta(x) 为

 

 

 

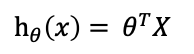2. 梯度下降

梯度下降算法， 查找最优参数（Gradient descent）

拥有函数 J(theta0, theta1),  该函数的最小值是多少？

 

2.1 对单个变量梯度下降

想法：

将theta0, theta1 变成0

不断的变化theta0, theta1的值，并计算出 J(theta0, theta1)的值，并取最小值。

直到算出最小值为止。

 

 

对于两个参数的J， 可能出现的值如下

 

 

 

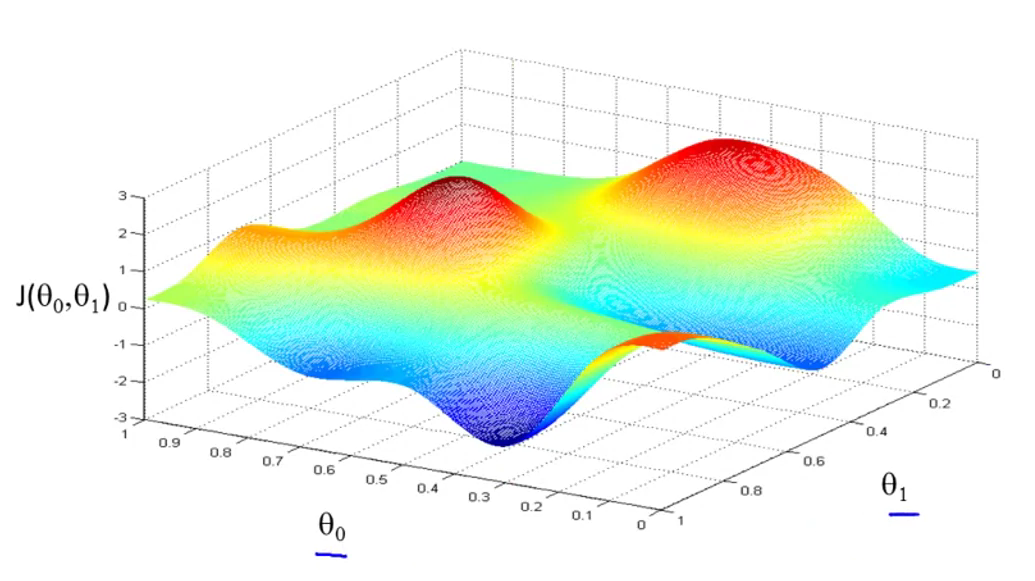
梯度下降算法

 

 

其中 ：= 是赋值的意思

alpha 是学习速率的意思

如果学习速率太慢， 则会降低学习速度

如果学习太快， 则可能导致无法收敛

 

偏导数计算过程如下：

 

 

对整个式子进行展开得到如下

 

 

 

 

当theta0 为0，只有一个参数theta1 时， J(theta1) 有如下公式

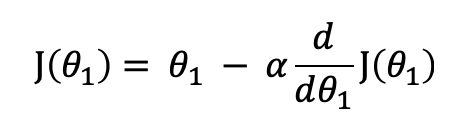只有一个参数，相当于在求该点的导数，如下图所示

 

 

当点theta1在右测时，导数值是一个大于零的数， theta1 的值逐渐梯减

 

 

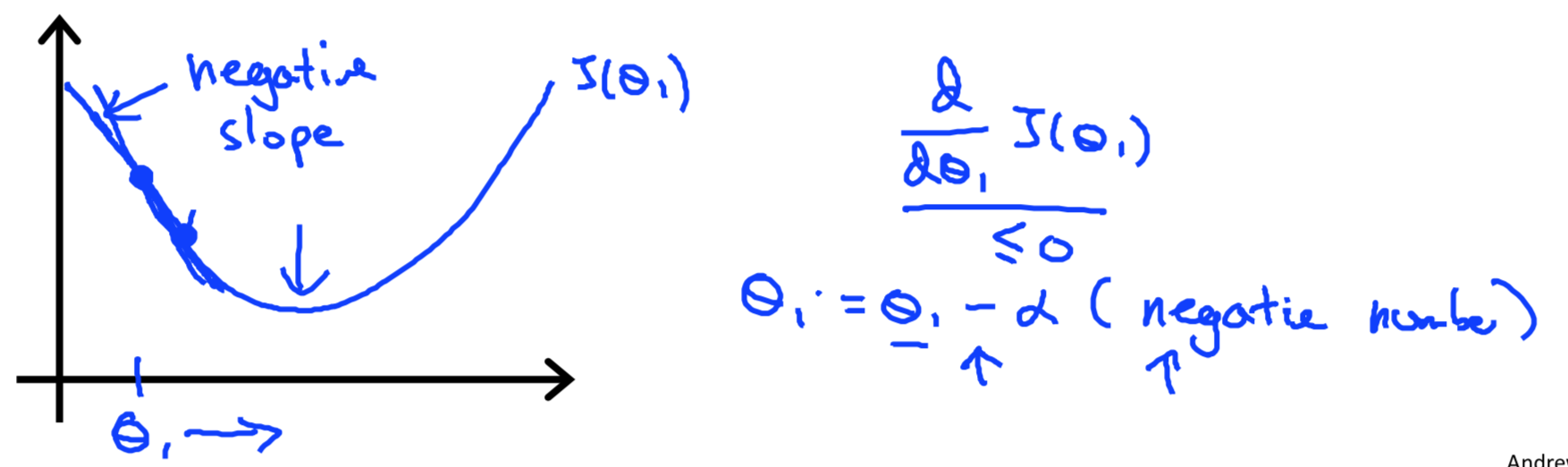
当点theta1在左测时，导数值是一个大于零的数， theta1 的值逐渐梯增

 

 

2.2 对多个变量梯度下降

多变量的损失函数如下

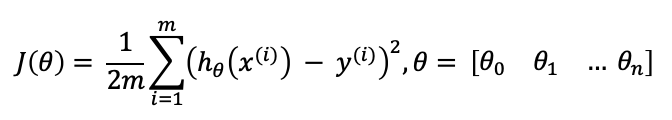梯度下降算法形式如下

 

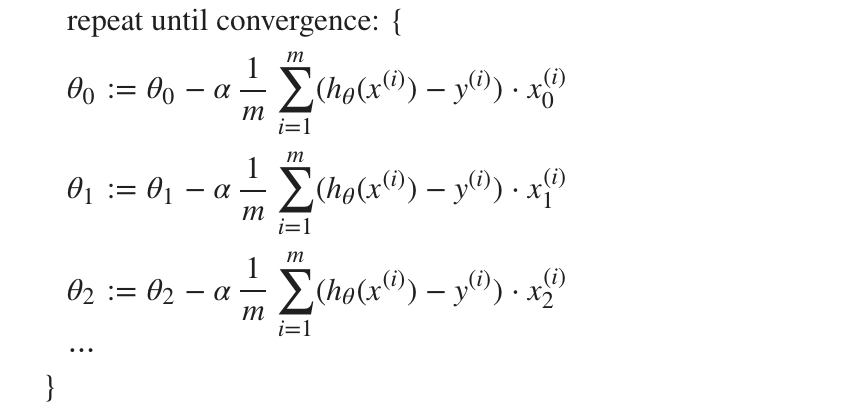抽象化

 

 

单变量与多变量对比

 

2.3 梯度下降优化

1. 特征缩放，去除（最大值 - 最小值），最好将每个特征的值放在 -1 到 1之间

2. 均值归一化，减去均值

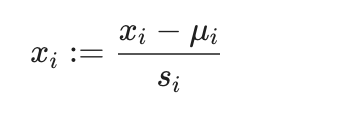mu_i 表示所有特征的均值， s_i 表示特征值的范围，最大值 - 最小值

 

 

3. 正规方程解

3.1 线性代数基础

矩阵是一个二维数组(m * n), 当 m 或 n 为1时， 则是向量

 

在octave中运行

% The ; denotes we are going back to a new row.
A = [1, 2, 3; 4, 5, 6; 7, 8, 9; 10, 11, 12]

% Initialize a vector 
v = [1;2;3] 

% Get the dimension of the matrix A where m = rows and n = columns
[m,n] = size(A)

% You could also store it this way
dim_A = size(A)

% Get the dimension of the vector v 
dim_v = size(v)

% Now let's index into the 2nd row 3rd column of matrix A
A_23 = A(2,3)

 

 

矩阵加减法： 矩阵中的每个值分别对应相加减

 

矩阵与向量相乘，规则如下

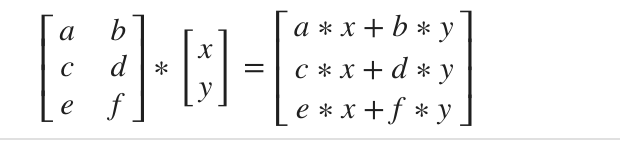可以解决一元线性方程

 

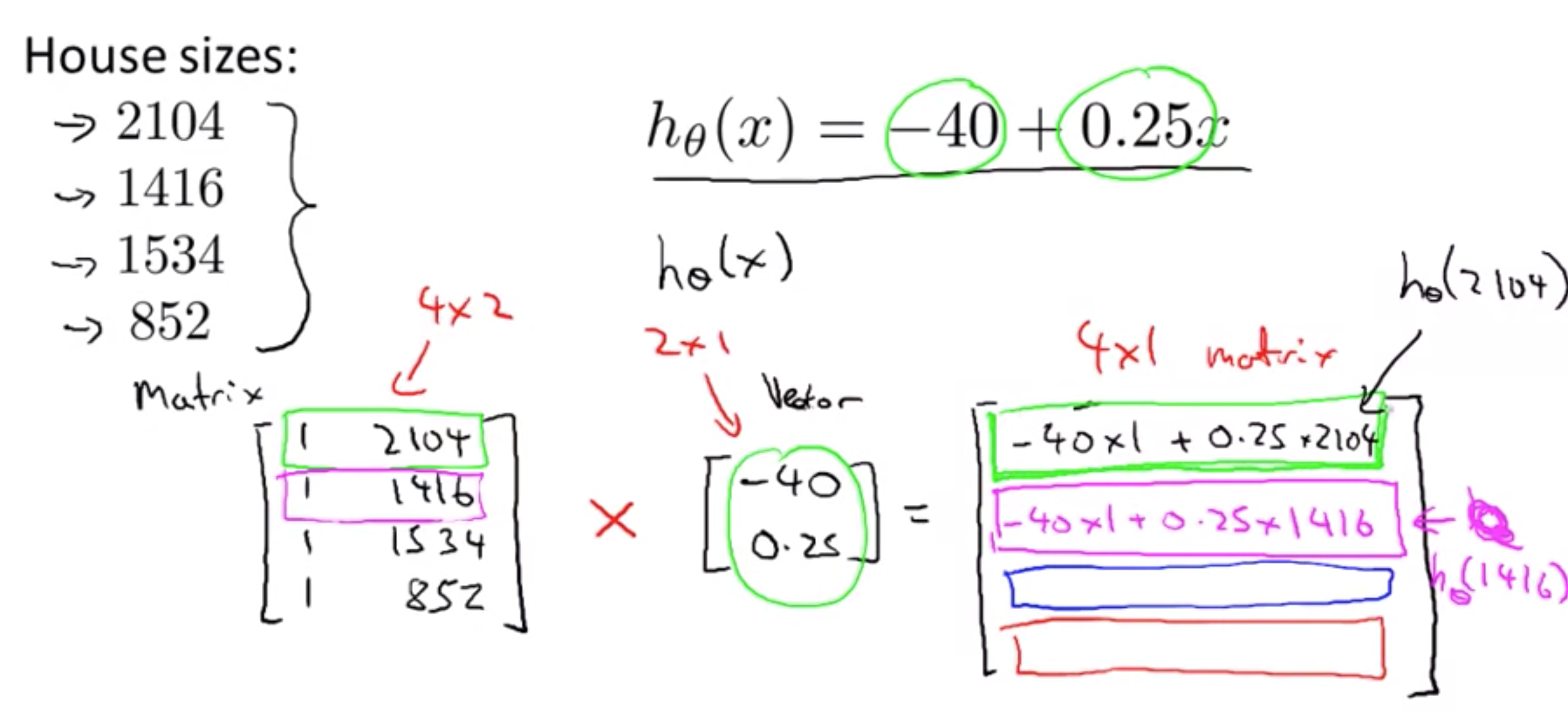代码运行如下

% Initialize matrix A 
A = [1, 2, 3; 4, 5, 6;7, 8, 9] 

% Initialize vector v 
v = [1; 1; 1] 

% Multiply A * v
Av = A * v

 

 

运行结果

A =

   1   2   3
   4   5   6
   7   8   9

v =

   1
   1
   1

Av =

    6
   15
   24

 

 

 

矩阵与矩阵相乘，相乘法则如下

 

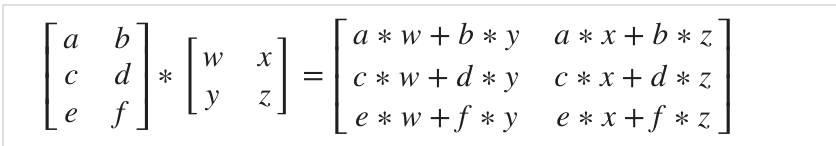可以解决多个

 

 

 

矩阵特性：

矩阵不符合交换律： AB != BA

矩阵符合结合律： ABC = A(BC)

任何矩阵与单位矩阵相乘，结果为本身。

 

% Initialize random matrices A and B 
A = [1,2;4,5]
B = [1,1;0,2]

% Initialize a 2 by 2 identity matrix
I = eye(2)

% The above notation is the same as I = [1,0;0,1]

% What happens when we multiply I*A ? 
IA = I*A 

% How about A*I ? 
AI = A*I 

% Compute A*B 
AB = A*B 

% Is it equal to B*A? 
BA = B*A 

% Note that IA = AI but AB != BA

 

 

运行结果

A =

   1   2
   4   5

B =

   1   1
   0   2

I =

Diagonal Matrix

   1   0
   0   1

IA =

   1   2
   4   5

AI =

   1   2
   4   5

AB =

    1    5
    4   14

BA =

    5    7
    8   10

 

 

矩阵转置

Aij = Bji

 

矩阵逆运算

A-1 * A = I

 

代码如下：

% Initialize matrix A 
A = [1,2,0;0,5,6;7,0,9]

% Transpose A 
A_trans = A' 

% Take the inverse of A 
A_inv = inv(A)

% What is A^(-1)*A? 
A_invA = inv(A)*A

 

 

运行结果

A =

   1   2   0
   0   5   6
   7   0   9

A_trans =

   1   0   7
   2   5   0
   0   6   9

A_inv =

   0.348837  -0.139535   0.093023
   0.325581   0.069767  -0.046512
  -0.271318   0.108527   0.038760

A_invA =

   1.00000  -0.00000   0.00000
   0.00000   1.00000  -0.00000
  -0.00000   0.00000   1.00000

 

3.2 正规方程解

 

 

梯度下降 VS 正规方程解

Gradient Descent	Normal Equation
Need to choose alpha	No need to choose alpha
Needs many iterations	No need to iterate
O (kn^2kn2)	O (n^3n3), need to calculate inverse of X^TXXTX
Works well when n is large	Slow if n is very large

 

4. Octave 基础

 

4.1 基础运算

octave>1 + 2
ans =  3
octave>3 - 2
ans =  1
octave>1 * 2
ans =  2
octave>1 / 3
ans =  0.33333
octave>2^10
ans =  1024
octave>1 == 2
ans = 0
octave>1 ~= 2
ans = 1
octave>1 && 0
ans = 0
octave>1 || 0
ans = 1
octave>