描述统计学

 

1. 简介

本篇文章是对描述统计学的一个总结概要

* 描述了统计学中的数据类型

* 分析数据时用到的统计学方法

* 如何测量集中趋势和离散程度

* 常见的数据形状

* 如何处理异常数值

* 如何构建可视化图表更好的表达数据

 

1.1 什么是数据？

文字、图像、视频、声音等和其他形式都是数据。分析数据可以让我们更好的理解事情的本质。帮助我们更好的决策。

 

一些概念：

随机变量，其值随机会而定的变量

随机事件，其发生与否随机会而定的事件

确定性变量，其值遵循某种严格的规律的变量

 

 

1.2 数据类型

有两种主要的数据类型

* 数值数据： 可以用来执行数学计算

* 分类数据： 标记一个群体或一组条目

 

将分类数据进一步划分，可以分为

分类定序：数据有排名顺序（排列问题，有两步，先取，后排）

分类定类： 数据没有排序或排名（组合问题，一步，取出即可）

 

排列公式

 

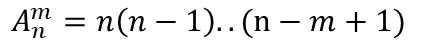组合公式

 

 

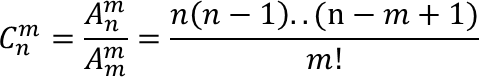数值数据进一步划分，可以分为

连续数据：可以分为更小的单位，并且仍然存在更小的单位。一个例子就是狗的年龄 - 我们可以以年、月、日、小时、秒为单位测量年龄，但是仍然存在可以与年龄关联的更小单位。

离散数据： 数据仅采用可数值。

 

 

1.3 概括统计

集中趋势测量告诉我们数据中一般情况

离散程度测量告诉我们数据之间的差异

 

分析数值数据的四个方面

* 集中趋势测量

* 离散程度测量

* 分布的形状

* 异常值

 

分析分类数据

分类数据的分析方法通常是查看落入每个组的独立个体的数量或比例。例如，如果我们在看狗的品种，我们会关心每个品种有多少只狗，或者每个品种的狗的比例如何。

 

集中趋势测量的方式有三种:

1. Mean 均值。 平均数
2. Median 中位数， 第一步，将数据排列，一半低于它， 一半高于它，对于偶数个数， 则是中间两个数的平均值
3. Mode 众数， 最常出现的值叫众数

 

随机变量用大写字母表示。每当我们观察到这些随机变量的一个结果，就用相同字母的小写表示。

 

数学符号平均值计算公

 

 

 

 

 

 

 

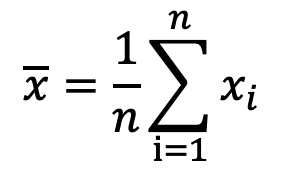
离散程度测量用于告诉我们数据之间的分散程度。常见的离散程度测量包括:

1. 极差，又称全距，是最大值和最小值之间的差值。
2. 四分位差 (IQR)，Q3​ 和 Q1​ 之间的差值。
3. 标准差，数据离散程度度量之一。它的定义为每个观察值与均值之间的平均差异。
4. 方差,

 

5数概括法

五数概括法包括 5 个值：

1. 最小值： 数据集中的最小值。
2. Q1​（第一四分位数）：排序后数据第 25% 处的值。
3. Q2​（中位数）：排序后数据第 50% 处的值。
4. Q3​（第三四分位数）：排序后数据第 75% 处的值。
5. 最大值： 数据集中的最大值。

 

方差公式

 

 

 

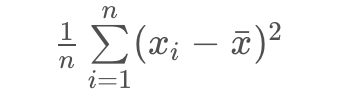
标准差公式

 

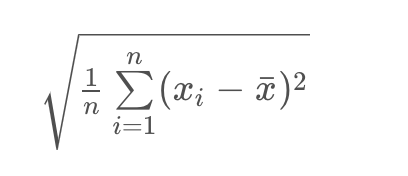* 方差和标准差都能用于比较两组不同数据的离散程度。方差/标准差较高的一组数据相比较低的一组数据，其分布更为广泛。

   但是注意，有可能只有一个（或多个）异常值提高了方差或者标准差，而大多数数据实际上比较集中。

* 在比较两个数据集之间的离散程度时，每个数据集的单位必须相同。

* 当数据与货币或经济有关时，方差（或标准差）更高则表示风险越高。

* 在实践中，标准差比方差更常用，因为它使用原始数据集的单位。

 

分布的形状如下图所示

* 右偏态

* 左偏态

* 对称分布

 

 

 

 

 

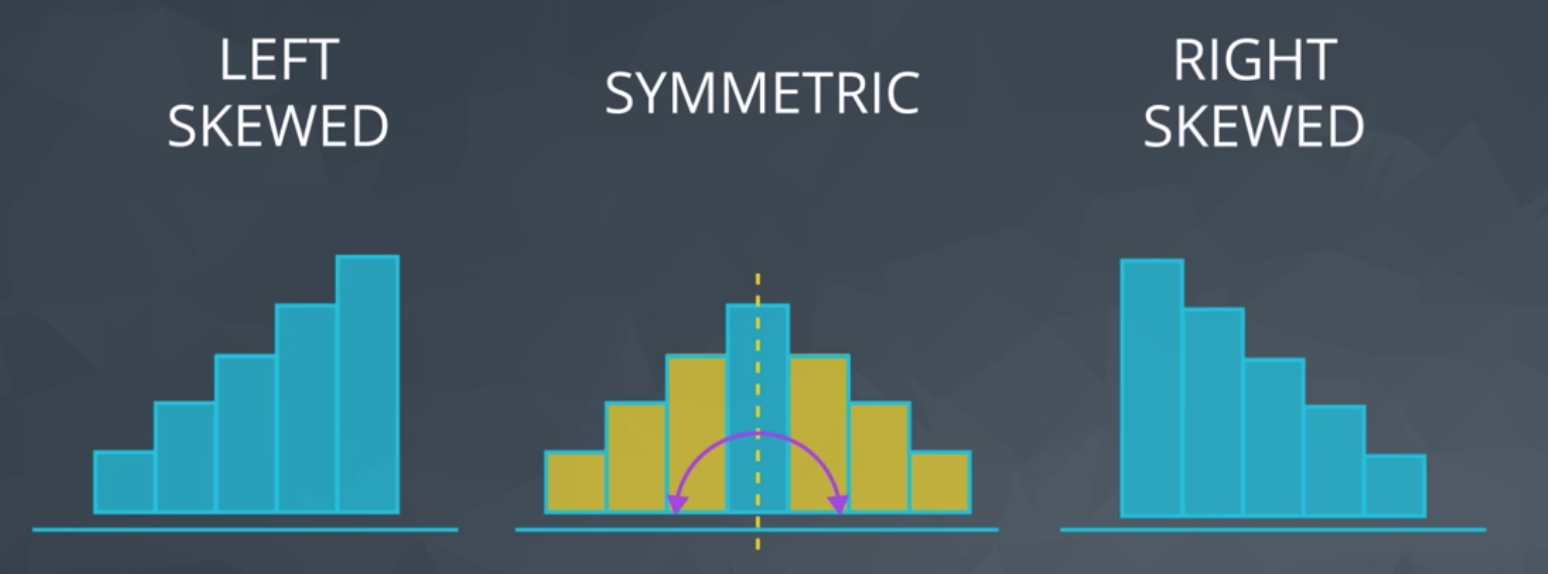
形状	均值与中位数	现实世界中的应用
对称（正态）	均值等于中位数	身高、体重、误差、降雨量
右偏态	均值大于中位数	血液中残留的药物量，呼叫中心的电话间隔时间，灯泡多久熄灭
左偏态	均值小于中位数	许多大学的成绩百分比，死亡年龄，资产价格变动

分布中的众数基本上是直方图中最高的直条。根据直方图中的最高峰数量，可能有多个众数。

 

 

异常值

异常值是明显偏离我们其余数据点的点。这会极大地影响均值和标准差等度量，而对五数概括法中的第1四分位数、中位数、第2四分位数的影响较小。

 

如何处理异常值

当出现异常值时，我们应该考虑以下几点。

1. 注意到它们的存在以及对概括性度量的影响。

2. 如果有拼写错误 —— 删除或改正。

3. 了解它们为什么会存在，以及对我们要回答的关于异常值的问题的影响。

4. 当有异常值时，报告五数概括法的值通常能比均值和标准差等度量更好地体现异常值的存在。

5. 报告时要小心。知道如何提出正确的问题。