01. 什么是人工智能
1. 基本概念
定义
机器学习是一门研究如何通过计算手段, 利用经验提升自身性能的学科。
人工智能、机器学习与深度学习三者间的关系如图1-1所示
|
图 1-1 概念间关系 |
1.1 人工智能定义
努力将通常由人类完成的智力任务自动化。
1.2 机器学习定义
是一种新的编程范式, 传统编程范式如图 1-2 所示

图1-2 传统的编程范式 |
机器学习的编程范式

图1-3 机器学习编程范式 |
机器学习的定义:在预先定义好的可能性空间中,利用反馈信号的指引来寻找输入数据的有用表示。
这个简单的想法可以解决相当多的智能任务,从语音识别到自动驾驶。
一个程序可以从经验E中学习,解决任务T, 达到性能度量值P, 当且仅当有了经验E过后,经过P评判,程序在处理T时性能有所提升。(Tom Mitchell, 1998)

图1-4 机器学习编程范式 |
机器学习可以分成两部分:根据是否有标签
* 监督式学习: 知道使用法则可以在输入与输出之间输出数据。
* 非监督式学习: 当不知道结果的时候
监督式学习算法可以分成
* 回归问题
* 分类问题
非监督式学习算法
聚类
1.3 深度学习
对深度的定义
从数据中学习表示的一种数学框架,强调从连续的层中进行学习,这些层对应于越来越有意义的表示。
“深度学习”中的“深度”指一系列连续的表示层,数据模型中包含多少层,这被称为模型的深度(depth)。
图1-4, 一个数字分类的深度学习网络框架

图 1-4 用于数字分类的深度神经网络 |
深度学习: 学习数据表示的多级方法。
深度学习从数据中进行学习时有两个基本特征:
第一, 通过渐进的、逐层的方式进行越来越复杂的表示;
第二,对中间这些渐进的表示共同进行学习,每一层的变化都需要同时考虑上下两层的需要。
强化学习:
通过不断的试错进行学习
1.4 发展历程
20世纪五十年代中后期,“连接主义”
20世纪五十年代至七十年代,人工智能研究处于推理期,典型代表,逻辑理论家,通用问题求解
20世纪七十年代中期,人工智能进入知识期
与此同时,基于逻辑的“符号主义”
机器学习研究划分为
* 从样例中学习
* 在问题求解和规划中学习
* 通过观察和发现学习
* 从指令中学习
20世纪80年代以来,被研究最广的为从样例中学习,涵盖了监督学习与无监督学习等。
20世纪90年代中期,统计学习,代表技术是支持向量机,与枋方法
21世纪初, 连接主义卷土重来,以深度学习为名的热潮,即有很多层的网络。
2. Hello World Deep Learning
观察如下一组数据
| x = | -1 | 0 | 1 | 2 | 3 | 4 |
| y = | -3 | -1 | 1 | 3 | 5 | 7 |
发现规律: y = 2x - 1
如果使用传统方案编程, 很容易得出想要的结果y的值。
cal(int x) { return 2 * x -1; }
现在使用深度学习模型来计算出 y = 2x - 1 这个算法,即通过机器去观察这组数据,
得出这个算法。
cal (int x) { 深度学习模型 return y; }
为了能让该模型正常工作,在使用深度学习模型之前 , 必须要使用样本数据来训练该模型。
2.1 环境搭建
mkdir src python3 -m venv venv pip install tensorflow pip install numpy pip install matplotlib
2.2 代码coading
第一步,导入需要的包
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt
第二步,设置训练模型数据
# set up training data x = np.array([-1, 0, 1, 2, 3, 4], dtype=int) y = np.array([-3, -1, 1, 3, 5, 7], dtype=int) for i,c in enumerate(x): print("x = {} , y = {}".format(c, y[i])
运行结果:
x = -1 , y = -3
x = 0 , y = -1
x = 1 , y = 1
x = 2 , y = 3
x = 3 , y = 5
x = 4 , y = 7
第三步, 创建层
# step 1 build the layer first_layer = tf.keras.layers.Dense(units=1, input_shape=[1])
# step 2 assemble layers into model
model = tf.keras.Sequential([first_layer])
神经网络的核心组件是层, 所以创建模型中第一步就是构建层,层是一种数据过滤器。
每层过后就是更有用的信息。
不同的张量格式与不同的数据处理类型需要用到不同的层。
例如
简单的向量数据保存在形状为(samples, features)的 2D 张量中, 通常用密集连接层来处理
序列数据保存在形状为(samples, timesteps, features)的 3D 张量中, 通常用循环层(LSTM, recurrent Layer)来处理。
图像数据保存在4D张量中,通常用二维卷积层(Keras 的 Conv2D)来处理。
第四步: 编译模型
# complie the model model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(1))
编译模型需要三个参数:
* 损失函数(loss function): 网络如何衡量在训练数据上的性能,具有多个输出的神经网络可能具有多个损失函数。
定义损失函数有一些指导原则:
对于二分类问题,使用二元交叉熵损失函数
对于多分类问题,可以用分类交叉熵损失函数
对于回归问题,可以用均方误差损失函数
对于序列学习问题,可以用联结主义 时序分类(CTC,connectionist temporal classification)损失函数,等等。
* 优化器(optimizer): 基于训练数据和损失函数来更新网络的机器
* 在训练和测试过程中需要监控的指标(metric)
模型是由层构成的网络,深度学习模型是层构成的有向无环图。
常见的网络拓扑结构如下:
* 双分支(two-branch) 网络
* 多头(multihead)网络
* Inception 模块
第四步:训练模型
# train the model print("start training the model") history = model.fit(x, y, epochs=500, verbose=False) print("Finished training the model")
第五步:查看模型统计数据
# show training statistics plt.xlabel('Epoch Number') plt.ylabel("Loss Magnitude") plt.plot(history.history['loss'])
plt.show()
运行结果
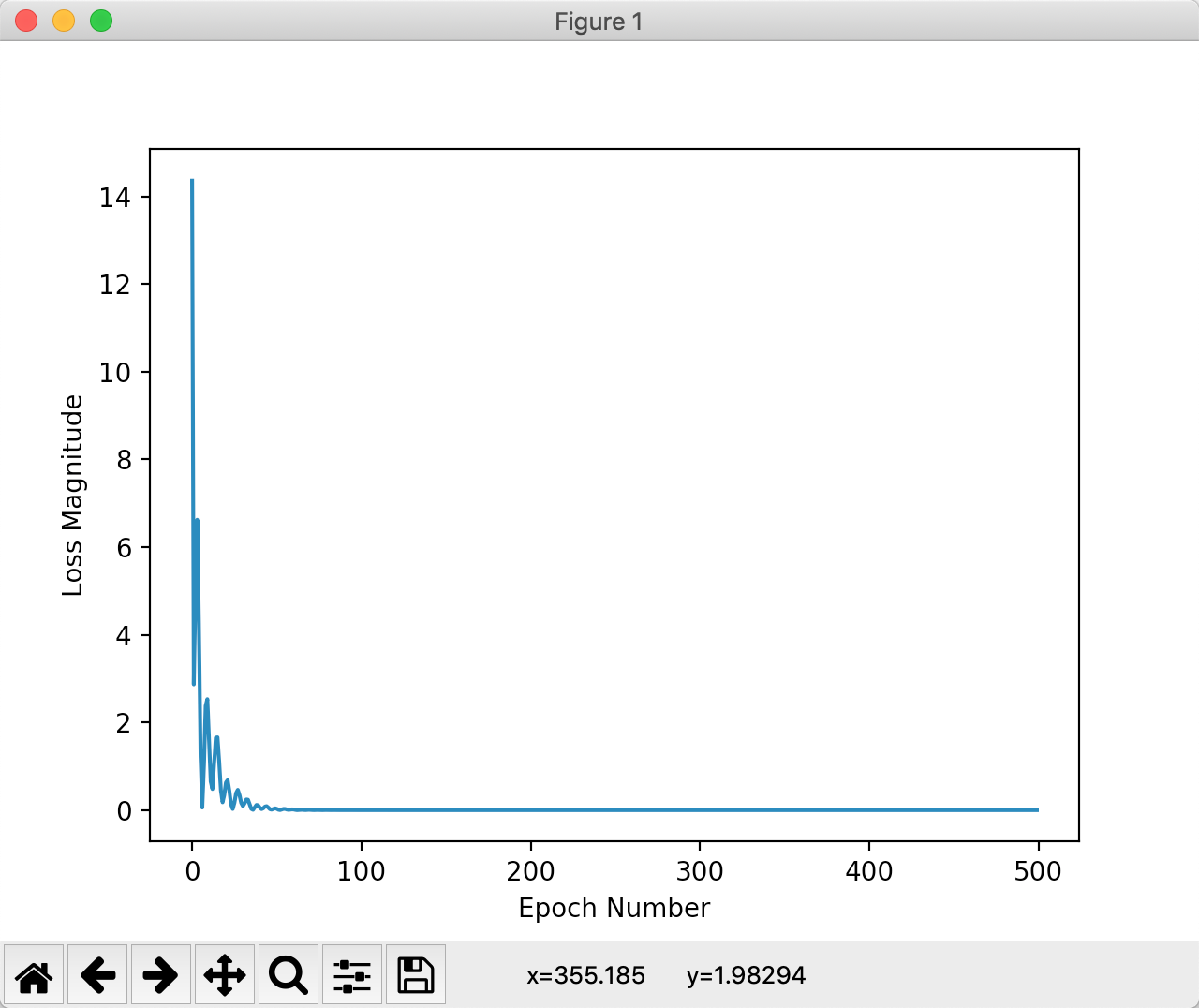
图2-1 运行结果 |
解释一下过拟合(overfit)的概念:
机器学习模型在新数据上的性能往往比在训练数据上要差。
第六步:使用测试数据测试结果
# use the model predict values print(model.predict([100]))
运行结果
[[199.]]
第七步:查看模型权重信息
# show layer weights print("These are the layer variables: {}".format(first_layer.get_weights()))
运行结果
These are the layer variables: [array([[2.]], dtype=float32), array([-1.], dtype=float32)]
典型的Keras工作流程:
(1) 定义训练数据: 输入张量和目标张量, 有两种方法(Sequential , API function)
(2) 定义层组成的网络(或模型), 将输入映射到目标
(3) 配置学习过程: 选择损失函数、优化器和需要监控的指标。
(4) 调用模型的fit方法在训练数据上进行迭代。
3. 深度学习工作原理
机器学习是将输入映射到目标,这一过程是通过观察许多输入与目标示例完成的。比如 x 与 y 值。
神经网络中每层对输入数据所做的具体操作保存在该层的权重中,其本质是一串数字,由其来进行参数化。
所以权重也被称为该层的参数。在这种情况下, 学习的意思就是找出该层的权重值,使得网络能够将每个示例
输入与其目标正确地一一对应。 流程如图3-1所示

图3-1 深度学习网络由权重来参数化 |
问题来了, 一个深度神经网络可能有数千万个参数,找到正确的取值是一项艰巨的任务。
神经网络中损失函数的定义
衡量预测值y' 与 预期值 之间的距离, 算出损失值。

图3-2 损失函数用来衡量网络输出的质量 |
例如如下一个线性回归的问题
|
图3-3 数据图表, 蟋蟀叫的声音次数与温度之间的关系 |
使用一根直线可以近似的描述这个每分钟叫声与温度之间的关系

|
事实上,虽然该直线并未精确无误地经过每个点,但针对我们拥有的数据,清楚地显示了鸣叫声与温度之间的关系。
只需运用一点代数知识,就可以将这种关系写下来,如下所示:
y = mx + b
其中:
y 指的是温度(以摄氏度表示),即我们试图预测的值。
m 指的是直线的斜率。
x 指的是每分钟的鸣叫声次数,即输入特征的值。
b 指的是 y 轴截距。
使用机器学习的方程式
y' = b + w1x1
其中:
y′ 指的是预测值(理想输出值)。 b 指的是偏差(y 轴截距)。在一些机器学习文档中,它称为 w0。 w1 指的是特征 1 的权重。权重与上文中用 m 表示的“斜率”的概念相同。 x1 指的是特征(已知输入项)。
要根据新的每分钟的鸣叫声值 x1 判断(预测)温度 y′,只需将 x1 值代入此模型即可。
下标 w1x1 是一个抽象概念, 可以用多个特征来表示更加复杂的模型。
例如有三个特征的模型可以采用以下方程来表示
y' = b + w1x1 + w2x2 + w3x3
损失值是一个数值,表示对于单个样本而言模型预测的准确程度。如果预测模型完全正确, 则损失值为0,
否则值越大,表示偏差越大。
训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差。
损失函数
(1) 平方损失 (L2损失)
定义如下:
(真实值 - 预测到的值)2 = (y - y')2
(2) 均方误差损失(MSE)
 |
其中:
(x,y) 指的是样本,其中
x 指的是模型进行预测时使用的特征集(例如,温度、年龄和交配成功率)。
y 指的是样本的标签(例如,每分钟的鸣叫次数)。
prediction(x) 指的是权重和偏差与特征集 x 结合的函数。
D 指的是包含多个有标签样本(即 (x,y))的数据集。
N 指的是 D 中的样本数量。

比较两张图哪个均方误差较高 |
左侧的图
线上的 6 个样本产生的总损失为 0。不在线上的 4 个样本离线并不远,因此即使对偏移求平方值,产生的值仍然很小:

右侧的图
线上的 8 个样本产生的总损失为 0。不过,尽管只有两个点在线外,但这两个点的离线距离依然是左图中离群点的 2 倍。
平方损失进一步加大差异,因此两个点的偏移量产生的损失是一个点的 4 倍。

优化器的定义
深度学习利用这个操作值,使用优化器函数来进行对权重值进行微调。
优化器中使用了反向传播算法,是深度学习的核心算法, 一种利用梯度下降优化来训练一系列参数化运算链的方法。

图3-3 将损失值作为反馈信号来调节权重值 |
通过迭代方法降低损失, 不断的更新, 最终会得出一个越来越接近y的预期值。
对于回归问题产生的损失值是一个碗形,所以肯定可以找到一个损失最小的值。

|
但是通过该方法需要大量的计算资源,另一种方法叫做梯度下降法
梯度下降法来降低损失, 可以减少计算的次数

|
可以看到, 降低损失是由学习速率与执行的步骤决定的。

|
梯度下降法的第一个阶段是为 w1 选择一个起始值(起点)。起点并不重要;因此很多算法就直接将 w1 设为 0 或随机选择一个值。
然后,梯度下降法算法会计算损失曲线在起点处的梯度。简而言之,梯度是偏导数的矢量;
它可以了解哪个方向距离目标“更近”或“更远”。请注意,损失相对于单个权重的梯度就等于导数。
学习速率降低可能会导致学习时间过长。

|
随机梯度下降法(SGD)

|
包含随机抽样样本的大型数据集可能包含冗余数据。实际上,批量大小越大,出现冗余的可能性就越高。
一些冗余可能有助于消除杂乱的梯度,但超大批量所具备的预测价值往往并不比大型批量高。
如果我们可以通过更少的计算量得出正确的平均梯度,会怎么样?通过从我们的数据集中随机选择样本,我们可以通过小得多的数据集估算(尽管过程非常杂乱)出较大的平均值。
随机梯度下降法(SGD) 将这种想法运用到极致,它每次迭代只使用一个样本(批量大小为 1)。如果进行足够的迭代,SGD 也可以发挥作用,但过程会非常杂乱。“随机”这一术语表示构成各个批量的一个样本都是随机选择的。
小批量随机梯度下降法(小批量 SGD)是介于全批量迭代与 SGD 之间的折衷方案。小批量通常包含 10-1000 个随机选择的样本。小批量 SGD 可以减少 SGD 中的杂乱样本数量,但仍然比全批量更高效。
4. Keras, TensorFlow, Theano, CNTK

图4-1 深度学习软件栈与硬件栈 |
TensorFlow API 层次

|





