班课4
1. non-word spelling errors
error指任何不在字典中的word,修正的方式是产生一系列候选名单,选择其中最好的
选择方式有两种,第一个是shortest weighted edit distance,另一个是highest noisy channel probability
第一个是判断从错误的单词到正确的单词所做出的大小幅度,第二种是是这个单词的概率是最高的
2. 针对第一种方法引入Damerau-Levenshtein edit distance,计算两个单词之间的距离
分别统计四种操作,分别是insertion、deletion、substitution替换、transposition of two adjacent letters相邻的交换顺序
3. 上面的第二种方法是计算candidates在文中出现的频率,选择出现频率最高的
4. channel model probability
P(x|w):给定w这个单词,对x进行修改的概率是多少
count即计算二者同时出现的次数

del[x,y]指计算xy被误写成x的次数,ins[x,y]指x被误写成xy的次数,sub[x,y]指计算x被误写成y的次数,trans[x,y]指xy被误写成yx的次数
5. noisy channel prob for acress即除了上面的概率,也要考虑单词出现在文章中的单词,即给P(x|w)乘以P(w)
6. Bigram language model:通过一系列单词,已知前一个,预测后一个单词出现的概率
P(a|b)*P(c|a)可理解为P(b a c)
7. real-word spelling errors:即单词被错写成另一个单词
对每一个单词产生一系列包含自己的candidate,分别计算,选择使整句话概率最高的句子
probability of no error:没有出现拼写错误的概率取决于application,即不修改的概率
需要修改的情况向刚才一样进行计算
0.90即10个单词出现一个错误,0.95即20个单词出现1个错误
8. 压缩优点
存放一个压缩的posting list,解压再使用比直接使用完整的要快
9. 压缩需要的两个定理
1)Heaps‘ Law:M = kT^b
用来衡量vocabulary与tokens的关系,tokens指文件中有多少单词,vocabulary是不包含重复的单词个数
通常k在30到100之间,b约等于0.5. 两边同时取log得到一个斜率为0.5的线性关系
2)Zipf's Law:频率的排名与频率的数值之间的关系,cfi=K/i
在frequency中排名第i的term,其出现的频率正比于i
举例来讲,若出现频率最高的单词出现了cf1次,则出现频率第二高的单词出现次数为cf1/2次,第三高的单词出现频率为cf1/3次
两边同时取log同样得到线性形式
10. 若是赋予每一个term一个20位的空间,对于没有这么长的单词会造成浪费,所以可以用dictionary-as-a string,将所有term连成一个string,将原始的term/posting pointer/frequency中的term替换成term pointer,pointer指向term开始的位置
则frequency 4bytes,posting 4bytes,term pointer 3 bytes,term平均8bytes,4+4+3+8=19,故而400K terms*19=7.6MB
若每个单词平均8bytes,字典里单词共400K个,则共有400K*8B=3.2MB。共需要的pointer数量为log以2为底3.2M的对数,即为3bytes。举例理解的话,若标记长度为7的字典,则7的表达为111,6为110。。。所需要的pointer个数用log求,就可以保证每个位置都有一个特殊的表示
11. 进一步压缩的话可以用blocking,即几个单词为一组形成block,四个term公用一个pointer
在每一个block里面增加表示后面几个字母代表一个单词的数字,如7代表后面7位属于同一个单词,从而减少空间的占用
这里的4只是一个合理值,如果整个string都作为一个block,可能检索的速度会非常慢(非blocking是tree所以速度较快,blocking会减慢速度)
从前没有blocking的时候,以block size为4而言,pointer所需要的空间为3*4=12bytes,但是现在不需要pointer,只需要增加表示位数的数字,即3+4=7bytes
12. 同一个block里面的term长得会很相似,所以可以进行front encoding
如第一个单词是auto,第二个单词是automata,我们将其改写为4,4,mata;即使用上面的4个字母,后面还有4个,为mata
下一个单词为automate,我们将其改为7,1 ,e,即为使用第二个单词的前面7个,即automat,后面还有一个字母e
partial 3 in 4 front encoding即对第一个以及最后一个单词进一步进行优化,因为第一个不需要前面信息,最后一个不需要知道后面有几位
13. 对于一些很罕见的单词,posting list会很短,所以term本身多占用一些空间没有关系,但是如the这种常见的,posting list会很长
第一种解决方法是using gap,即记录posting list的时候除了第一个的位置,后面的都是与前一个的差值,这样做的好处是将数值减小
对gap的压缩可以根据不同的单词采取不同压缩方法,如很罕见的单词可以用20 bits entry,而对于the这种常见的可以用1 bit entry
对于普通的单词,如果平均的gap是G,我们的gap entry就是log2G
variable length encoding指先转化为16进制,再将转化后的每一位数转化为2进制,然后相加。因为每行最多七位,所以从后往前数7位并在前面增加1表示code的最后一行,然后接着数7位,不到7位数字的用0补在前面,然后在前面加0表示不是code的最后一行如824为例
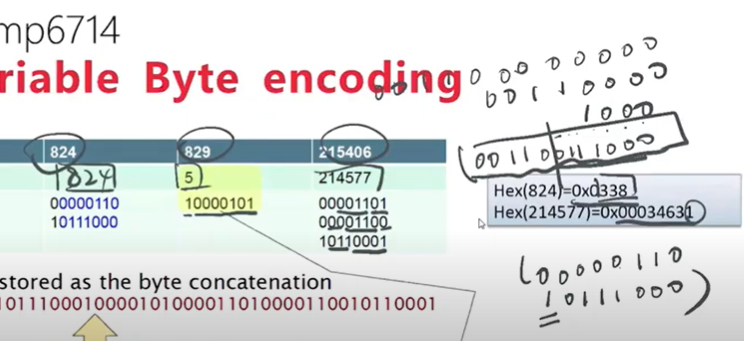
解码的时候注意补位的0,1不算。每行开头的0跟1相当于flag
14. simple9包含4位的selector以及28位的data bits
遇到一串gap的时候,计算gap最大的那个对应需要的编码数,查找对应的表格找到selector。data bits最多28个,每一段编码数固定,所以可能出现浪费1bit的情况
15. unary code
数字是几就是几个1,后面添加一个0,如3就是1110。0可以很好的对空间进行划分
16. Elias Gamma Code
Kd同时代表后面的Kr的位数
如255的Kd是7,用unary表示为11111110,同时7代表后面有7位,表示成127

解码很方便,从开始到第一个0都是Kd
17. 继续压缩的方法有Elias Delta code
因为Kd很大时,unary code会很长,方法是得到Kd与Kr之后,将Kd继续转化为Kdd与Krr

unary是控制长度的,即需要解码两次以缩短长度
18. Golomb code
定义一个参数b,首先假设其为2的k次方,根据公式求出q与r
因为r比b小,b需要k位,所以r也需要k位
q用unary表示,r用binary
b的选择比较好的是gap的均值*0.69。如果直接计算出来的数值就作为我们的b,这种方法是Golomb code,而rice code要求向下取整到2的次方
粉色框里的计算就是因式分解


 浙公网安备 33010602011771号
浙公网安备 33010602011771号