班课3
1. Karatsuba的算法中将大数分开,减少时间复杂度,但是若分的份数过多也会导致时间复杂度很高,所以引入the fast Fourier Transform
若有两个polynomial且最高次幂为n,将AB两部分合并成只有C,如下:
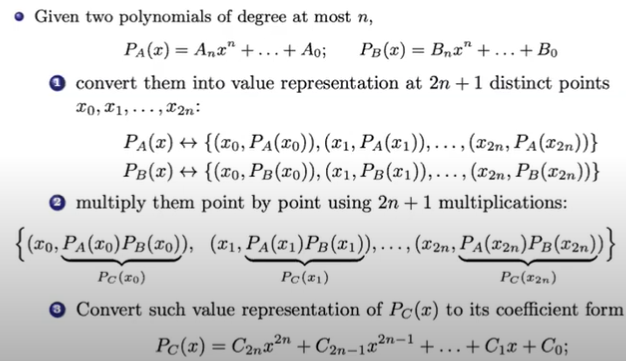
2. Complex number
若x轴表示实数,y轴表示虚数,则每个complex number都可以用一个向量(z=a+ib)表示
modulus为向量的长度以及arg(z)为与x轴的角度
z = |z|e^(i arg(z)) = |z|(cos arg(z) + i sin arg(z))
3. complex roots of unity
若z的n次方等于1,z一定存在5个解
第一点,转了n圈之后位置不变
第二点底数相同指数相加
第三点理解为减去尽可能多的n圈

4. DFT(the discrete fourier transform)
取A0到A(n-1)这n数分别作为polynomial前面的系数继而求complex roots of unity

5. 
需要FFT(fast fourier transform)计算PA(wnk), 时间复杂度为O(n logn)
6. FFT将polynomialPA(x)分为偶数次方与奇数次方的两部分,对奇数部分提取一个x出来,另y=x^2,得到新的polynomial,不断迭代
通过这种方式减少roots of unity
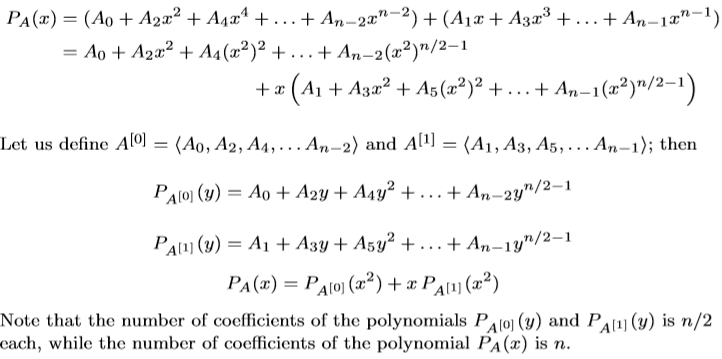

 浙公网安备 33010602011771号
浙公网安备 33010602011771号