final 2
1. inductive bias: 模型由于假定好的限制,不能跟真实的模型足够接近
如linear regression:假设target function是线性的;使用尽可能减小MSE来作为优化方向
nearest neighbor:假设function不能由一个简单的线性或非线性的function拟合;选取了唯一一种测量距离的方法
2. Bayes Theorem
P(D)通常被忽略

3. 如何用Bayes理论进行判断:选取概率更高的
a) MAP(Maximum a posterioir hypothesis), 即P(y=Ci|x)最大的即为所求
b) ML(Maximum likelihood, 即P(x|Ci)最大的即为所求
4. ∝表示正比例
bayes optical classifier: 有多个分类器,每个分类器都有一定的概率是准确的
举例来讲:


首先将hn(x)转化成P(-|hn)与P(+|hn) ———— 预测为正则+为1,-为0;反之相反
然后分别求+,-的概率(+:1*0.4+0*0.3+0*0.3,-同理)
比较+-中更大的那个的概率
5. Naive Bayes Classifier
x不仅有一个维度
假设所有feature,attribute之间都是独立的
假设总概率是不同维度下概率相乘
p(Vj)代表先前数据,如计算明天是否会羽毛球,p(Vj)即打或不大的概率;likelihood跟前面的计算类似,打以及不打分别计算(天气状况,温度等不同维度不同情况下的打/不打概率)
给出新的情况时,用先前概率乘对应情况下的概率,比较打与不大的概率,取最大值
6. zero frequency: 为避免概率为0,在原有数据基础上,每个数据都加1
7. 对于numeric attribute,与classification不同,先用高斯分布进行拟合,故而每个x都有与之对应的概率
8. Naive Bayes最重要的应用——text classification
bag of words: 忽略单词不同位置的影响,把句子理解为一个个set
一般有两种model,分别为multinomial与multivariate Bernoulli models
multivariate Bernoulli不考虑每个单词出现了几次,只关心是否出现过
同样增加advanced smooth,方法是新增加两行全是1和全为0的数据
Multinomial则需要对出现个数进行统计,对于相同类别内的数据进行混合,如class为+的情况有4种,a b c分别对应出现0,3,0次;0,3,3次;3,0,0次;2,3,0次。即class为+中,a出现5,b出现9次,c出现3次;同样增加advanced smooth,然后求概率
对于新出现的数据,出现n次就是概率的n次方
9. logestic regression
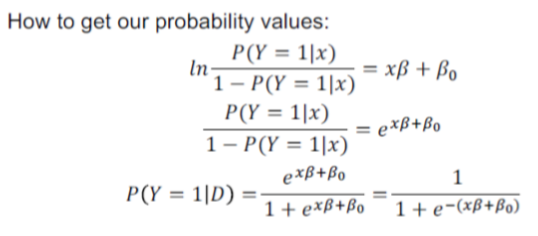
10. Occam's Razor
保证模型足够简单的前提下,越简单越好
![]()
11. decision tree
data是numeric features和discrete attribute的组合时,decision trees效果很好
目标function是离散的(即分类问题,否则采用regression trees)
12. important algorithm in Decisison Tree:TDIDT(Top-Down INducion of Decision Trees)
找到最好的一个feature进行split,在剩余的feature里,分别基于现有的两个class找到新的最好的feature
a) ID3(Iterative Dichotomiser 3)
针对categorical attribute
b) CaRT(Classification & Regression Tree)
支持categorical attribute与numerical attributes
13. Entropy
选取最好的feature的标准是希望结果尽量不均衡,即最好split之后的结果全为一类;衡量标准即为entropy(0 1之间)
![]()
14. information gain
比较原始数据的entropy与split之后所得数据的entropy的差值,越大越好
每一层split的店不一定一致
15. ID3优化可以得到gain ratio
由于有的attribute可以划分的特别细,故而split效果就很好,但是这对别的attribute是不公平的
增加splitEntropy: 划分的越细,SplitEntropy就越高
用GainRatio平衡两者,越大越好(即gain尽可能大。SplitRatio尽可能小

16. decision tree很容易overfitting
即有h, h'两个算法;training data上h的error小于training data上h'的data;所有数据上h的error大于h'的error;则h是overfitting的
17. overfitting的解决方法为pruning
a) pre-pruning: training没结束前就停下来
early stop,增添限制,如max_leaf_nodes; min_samples_split; max_depth
b) post-pruning: tree构建完成后逐层向上pruning
data分为train和valid两部分,用valid进行pruning
post-pruningk可以细分成: reduced-error Pruning; Minimum error; Samllest tree
reduced-error Pruning: 数据分为training与validation,通过training得到tree,然后在valid上逐层检测,如果某一点的split使效果反而变差了,则删除这个分支
缺点是data很少的情况下还要分一部分给valid,会使效果不好
minimum error:training时用cross-validation不断测试error,选取error最低的那个
smallest tree:考虑error的同时也要考虑tree的大小,即在可以接受的错误率范围中找到一个最小的
18. tree to rules

19. decision trees也可以解决continuous valued attribute,尽可能使class相同的分在一起

20. attr with costs
如做测试需要花钱,可以将gain修改为原来gain的平方/cost
21. windowing
解决training set过大的问题,只用一部分training data构建tree,用剩余data测试,若所有的training data都测试通过则结束,否则将测试错误的data放入window里面进一步测试
22. decision tree的inductive bias是只达到了局部最优,每一轮只选取了当前来讲最佳的;同时我们希望树的size越小越好,但是这种设定对于模型本身而言并不一定是最优解
24. decision tree优点:interpretability可解释性;测试很快;可以处理数据丢失;可处理无关attribute(Gain = 0);categorical以及numerical data均可处理
缺点是容易overfitting且不一定达到全局最优
25. regression tree
用weighted average variance做evaluation
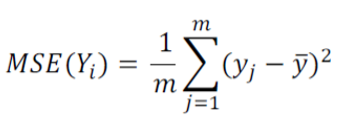

求weighted average variance即根据按照当前方法regression之后每个区间里data的占比,乘以对应MSE
选择最小的
26. model tree
regression tree的升级版本,每一个节点split后在两边分别做一个linear regression即线性回归,传递到下一层
用standard deviation reduction标准差evaluation,若拟合的足够好就不需要继续split了
27. Perceptron Learning
由一个加和与其判别函数组成(加和大于0输出1;否则输出-1)
weight用w = w + yixi更新
28. 一般用对偶方式解决:Duality
29. Perceptron Learning用kernel trick解决非线性问题
将x mapping到更高维上,如(x1, x2) --- (x2^2, x2^2, x1x2)
但是如果对mapping后的两个point做乘积会很花时间,所以可以先将x1 x2相乘
常见kernel trick有
a) polynomial kernel: K(x, x') = (x*x' + c)^q
b) RBF kernel: K(x, x') = exp(-||x-x'||^2/2a^2)
30. SVM
提高模型泛化能力,如果有很多limitation可以作为classifier,选取最宽的那个,宽度用margin表示
假设边界线为wx = t, 可以平移到最远的两个边界分别为wx = t+m, wx = t-m, 用法向量可以帮助计算margin
min 0.5*||w||^2化简得到yi(w*xi - t)>=1 即所有点都在线外,并使其最小化
解决用到Largangian multipliers
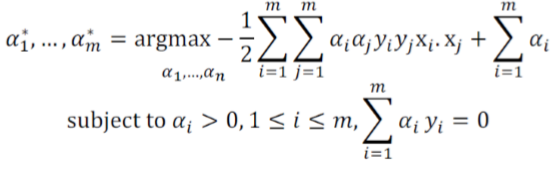
X'即x与y对应的乘在一起
X'X'T表示了不同组合的乘积,将其代入argmax的公式里
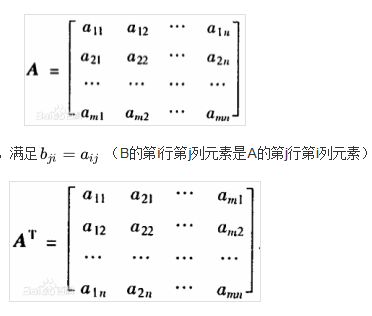
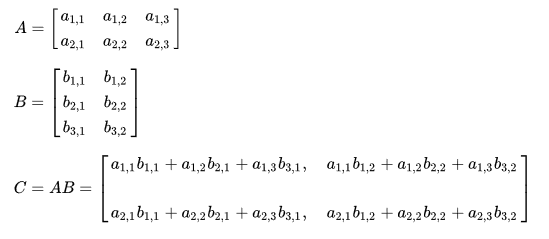
计算如下:

将a3去掉,然后分别对a1, a2求导使其等于0,解出a1, a2
然后求出w t(求t时需要support vector,即落在边界线上的一个点,这里即为an不为0的,把对应的xn代入,求t)
31. SVM也有kernel形式
32. Soft Margin SVM
ai = 0, 点在边界外面
0 < ai < C,support vector,边界上
ai = 3, 在margin里面或者边界上

 浙公网安备 33010602011771号
浙公网安备 33010602011771号