final 1
1. machine learning分类
supervised learning:output class is given (regression + classification)
unsupervised learning
2. regression预测的结果是一个连续的值,即对x y进行拟合
linear regression:假设拟合后的结果是一条直线 y = bx + c

θn对应xn前面的系数
y = θ0 + θ1x1 + θ2x2 + ... + θnxn = h(x)
首先定义一个误差函数MSE(mean squared error):
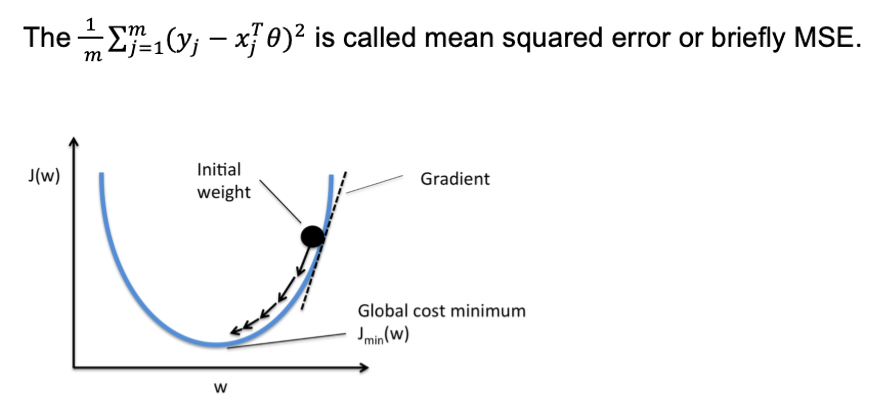
括号内内容为实际值-预测值,故而可理解为误差的平均表现,所以越小越好
3. 求MSE最小的情况——gradient descent
先不考虑所有m个情况,只对其中一个情况进行求导

最后一步中符号改变是因为所求梯度是向下梯度的反方向
4. Batch Gradient Descent指对一组所有梯度都求出来之后共同更新
Stochastic Gradient Descent指每一个点做完就进行一次更新
5. 除了gradient descent,linear regression还可以用closed-form solution解决
不需要迭代
var(x):方差

6. covariance
xn,yn分别于x, y的均值相比,若同大于或者同小于,则covariance为正,否则为负
反应x y之间是否存在正相关/负相关(正相关为+值,负相关为-值,没有什么相关性趋近于0)
correlation可理解为将范围为负无穷大到正无穷大的值压缩到-1到1的区间内

7. 用closed function得到的预测值与真实值差值之和为0
8. linear regression for curve shapes
使x2 = x1^2, x3 = x1^3。。。
故而保持线性方程的形式,但是这种赋值加的过少造成underfitting,过多造成overfitting
regularization:如何达到balanced,使J(θ)整体较小,其中前半部分表示误差,后半部分表示方程复杂程度,λ用于权衡后者的重要程度
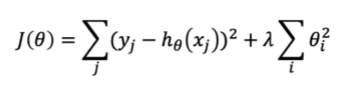
9. 同样的我们可以得到新的closed-form solution,也称之为ridge regression;若把式子中θi^2变为|θi|, 称该变形式为lasso
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
10. classification
最简单的一个模型:linear classification
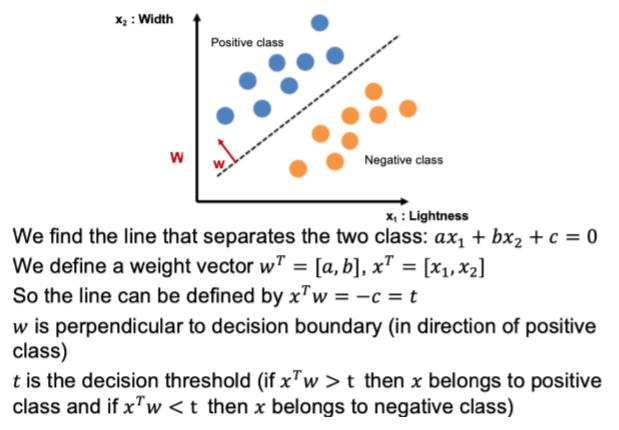
11. 首先找到两种类别的中心点(对于每个类别而言,分别求出横纵坐标的平均值),即p,n
p, n即为中心点也可以代表向量,用两者相减得到的w即为classification所求分割点的法线
故而已知分割线的法向量,以及分割线必定经过两中心点连线的中点,可求

12. 其他一些分类形式
a) generative algorithm
学习不同y下x分布的概率,可以产生新的数据
b) discriminative algorithm
对给出x,得到它属于y的概率(如:linear classification)
13. train data: 训练用的
validation data: 测试训练效果
test data: unseen data: 最后的测试,试验结束之后用的
14. batch learning:所有数据一开始就都给了
online learning:模型可以接纳新的数据
parametric:模型有固定数量的parameter
non-parametric:参数数量不固定的模型
15. cross-validation/out-of-sample testing
a) holdout method:直接中间分开

b) Leave-One-Out Cross validation(LOOCV)
分别让每一个元素作为test case,其他所有作为training case

选取均值作为评估模型的依据
c) K-fold Cross Validation
将数据分成K份,每次取出一份作为test,训练剩下的数据 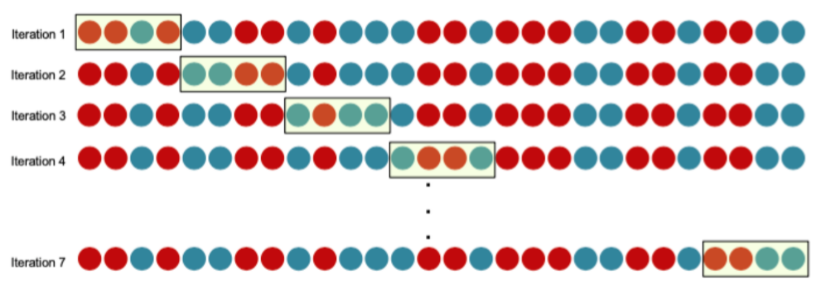
16. generalization
泛化能力,即训练结果可推广到别的数据上
deduction:将一个笼统的理念应用在一小部分数据上
induction:在部分数据上观测到一个结果,推广到通用的范围
17. data types
a) numerical
b) categorical: 一般情况下,categorical也会被转化为numerical形式
18. Normalization
训练前,先将数据压缩到同一个范围上去
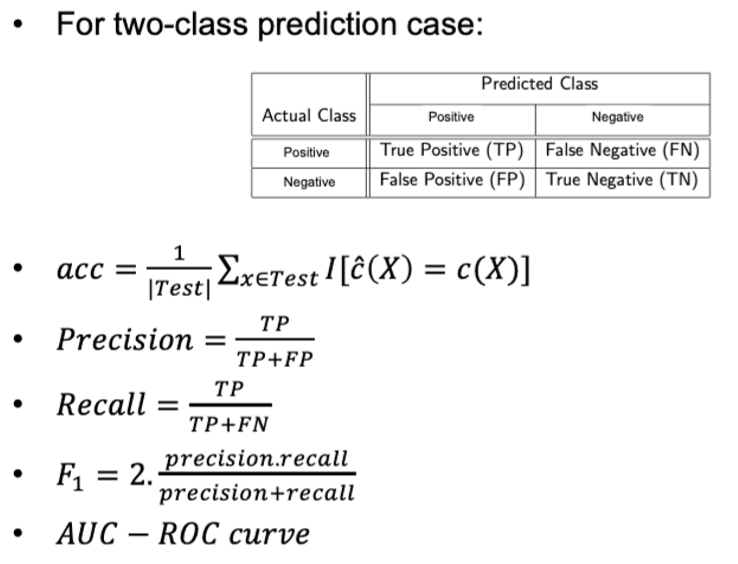
19. 对classification模型的评估
precision为预测为positive里,预测正确的概率;recall为实际为positive里,预测正确的概率
AUC-ROC curve是0到1之间的,越接近于1越好
20. 对regression模型的评估
RMSE,MAE均为越小越好,R-squared及其升级版越大越好

21. missing value
1)删掉有missing value的
很准确,但是大量数据丢失
2)用中值/中位数代替缺失值
数据量有限时比直接删除好,但是增加了variance与bias
如两条数据同时在某一位置缺失了一个值,若在其中都添加了中位数,可能增加了两条数据的相似性
3)将缺失的数据单独分到一类
跟(2)比起来没有添加过多variance
4)预测missing value
缺点是导致预测出来的值与用来预测它的值之间有较强的关联性
5)用支持missing value的算法
不用考虑相关性,但这种算法通常很耗时
22. nearest neighbor
将所有数据存储在一个数据空间里,距离很近的点之间有相似性
距离的计算如下

特殊情况还有,无穷大norm——Chebyshev distance: ![]()
0 norm即计算有几个维度里x y是不相同的: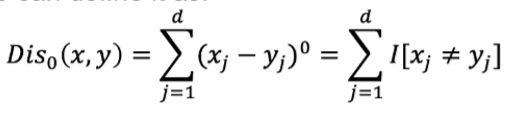
0 norm不完全属于P norm
如果x y是binary string,即为Hamming distance,计算将x转变成y需要改变几个bite (如0101--1111,hd=2)
23. distance需要满足distance metric
自己与自己之间距离为0
所有不同点之间距离大于0
距离是(symmetric)对称的,即xy,yx之间距离相同
满足三角不等式,两点之间直线最短(p<1时不满足该triangle inequality)
#若x不等于y时,x与y的距离可以是0,则为pseudo-metric
24. Nearest Centroid Classifier
只保存中心点,比较新的点与哪个中心点更近即可完成classification
简单快速,但是不准确
25. Nearest Neighbor
所有点都保留,找到新的点最近的1或几个点
若是nearest neighbor则只选择最近的点,所求点与之相同;K-Nearest neighbor则选取最近的K个点,classification的情况是对K个点进行统计,属于占比最多的class,regression则求邻居点的平均值
比24精确,但是很慢,要存储所有点,时间复杂度为O(n)
curse of dimensionality: 基于距离的方法,当x维度变大时,效果会变差。因为空间上距离的概念会越来越模糊
26. distance-weighted KNN
离所求点越近越重要,增加weight——距离平方的倒数
27. 对KNN的evaluation通常用到LOOCV,单独对每一个点进行训练求accuracy,然后求平均值
K=1时,training set error = 0,但是容易overfitting; K越大模型越稳定

 浙公网安备 33010602011771号
浙公网安备 33010602011771号