9020quiz总结
quiz 1
1. For all m,n ∈ ℕ>0 and all a,b ∈ ℤ: if a = b (mod m) and a = b (mod n) then a = b (mod mn)
answer: False
如17和5关于2同余1，关于4同余1，但是2*4=8，17和5不关于8同余
quiz 2
补充：空集与任何集合的笛卡尔积仍是空集
1.
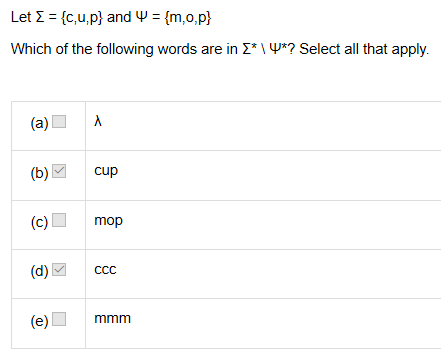
answer: b d
本题即求属于前者闭包且不属于后者闭包的，前者闭包包含{c,u,p,cc,uu,pp,cu...}，后者闭包包含{m,o,p,mm,mp...}
quiz 3
1. 
answer: d
本题的易错点是一定要为正整数
2. 
answer：a，e
function的定义有两点：
（1）binary
（2）在S到T的对应中，每一个s有且仅有一个t与之对应
f中有三个元素，故错误
若N={0,1,2,3}, a中等号over N相当于求N*N的笛卡尔积, {(0,0), (1,1), (2,2), (3,3)}，故而答案唯一
b中，(1,1), (1,2), (1,3)都有可能所以错误，c同理
3. 
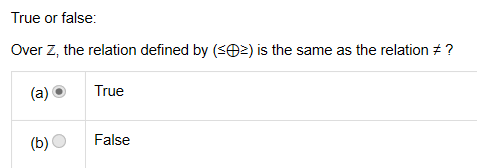
answer: a
注意异或的定义：(A\B) U (B\A)
quiz 4
补充：A\B=A与B的补集求并集
1. for all functions f X→Y and g Y→Z, if f and g are both surjective then gof is surjective
answer: True
gof为复合函数，可表示为g(f(x)), surjective为满射，证明满射即证明对任意z属于Z，存在x属于X使得g(f(x))=z
因为f, g均为满射，f(x)=y, g(y)=z, 所以g(f(x))=g(y)=z
2. for all functions f X→Y and g Y→Z, if f and g are both injective then gof is injective
answer: True
对于单射而言，对于任意a, b，if g(f(a))=g(f(b)), 则a=b是唯一的 (即output相同则input一定相同)
因为g单射故而f(a)=f(b), 因为f单射故而a=b
3. Consider the relation R = {(m,n)∈Z*Z : m^2=n^2(mod 5)}
a. Reflexivity
b. Antireflexivity
c. Symmetry
d. Antisymmetry
e. Transitivity
answer: ac
可写成5|m^2-n^2，即m^2-n^2=5k
ps: 还有一个题也是判断性质的，注意考虑为空的情况
quiz 5
1. 
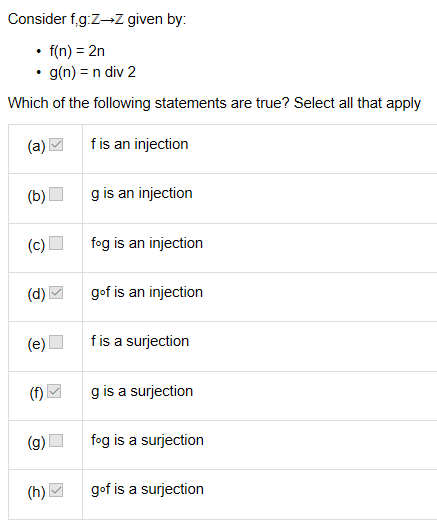
answer：a d f h
injection：
f是单射的，不同x对应不同y
g不是单射，反例为（3/2=1，2/2=1）
f∘g也不是，反例依然为3，2
g∘f是单射的
surjection:
f不是，因为其真实值域为全体偶数，而值域是全体整数集
g是的
f∘g真实值域也是全体偶数，所以不是
g∘f是的
2.
answer: a
f(n)<=f(n)必然成立，故A正确
R, AR是相对的，R成立即AR不成立
S可以找到不成立的情况，如f(n)恒等于3，g(n)=n, 当n大于3后，均符合f(n)<=g(n); f, g颠倒后，只有n小于3才成立，而定义域定义在全体实数上
AS反例：
T反例：在AS基础上再添加一个函数，使其幅度略高于黑线
3. 
answer：a c e
对于R，有零个情况满足，0也是自然数所以符合（有限多个）
对于AS的反例为：f恒为2，g除了一个元素等于1外其余也均为2
对于传递性，对于f,g只有有限个不相等，对于g,h也是只有有限个不相等，则f,h也只有有限个不相等，故而符合
quiz 6
1. 
answer: a b c d e f
sin(n)<=1∈O(1)∈O(n^2)
|n|<=n∈O(n)∈O(n^2)
b中依然可以忽略log部分，即O(n)
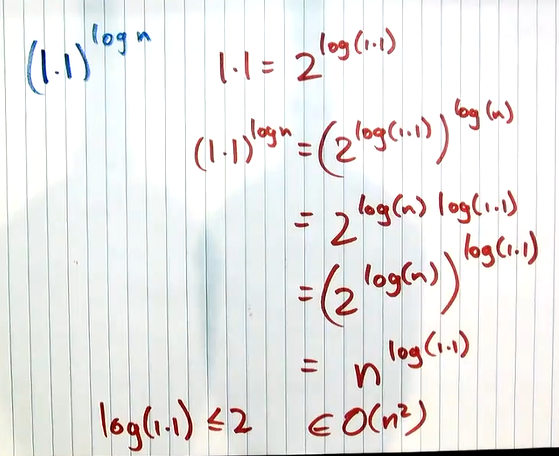
2. 
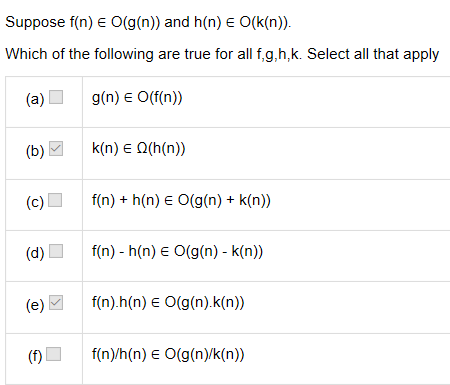
answer: b c e
f 的反例：f(n)=n^2=g(n), h(n)=n, k(n)=n^2
f/h=n, 大于1(g/k)
有关Big O，这里只考虑正数的情况
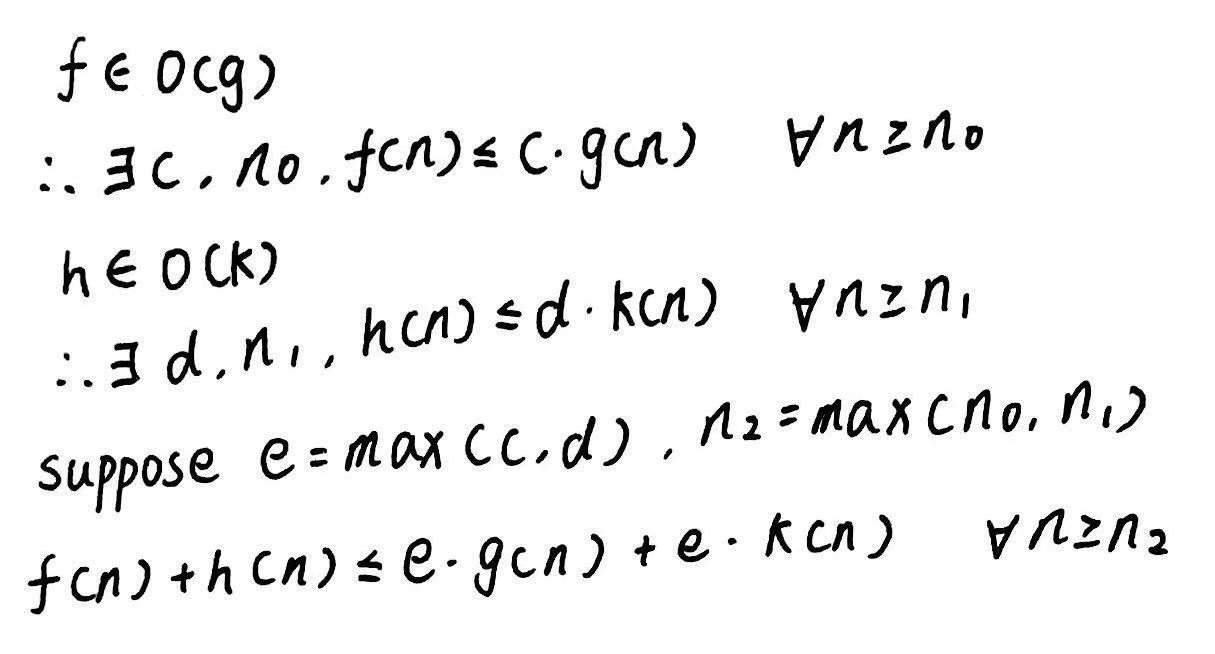
3. 
answer：a c
b错误，R不是partial order因为它不满足AS，如(n+2)∈O(n), n∈O(n+2), n+2!=n
4. 
第一个范围为（0，7), O(1)
第二个约为n^1.000001（log n很小）
第三个n^1.5
第四个n^1.99999
最后一个O(n^2)
quiz 7
1. 
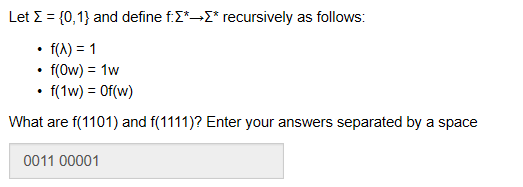
f(1101)=0f(101)=00f(01)=0011
f(1111)=0f(111)=00f(11)=000f(1)=0000f(λ)=00001
2. 
answer: c
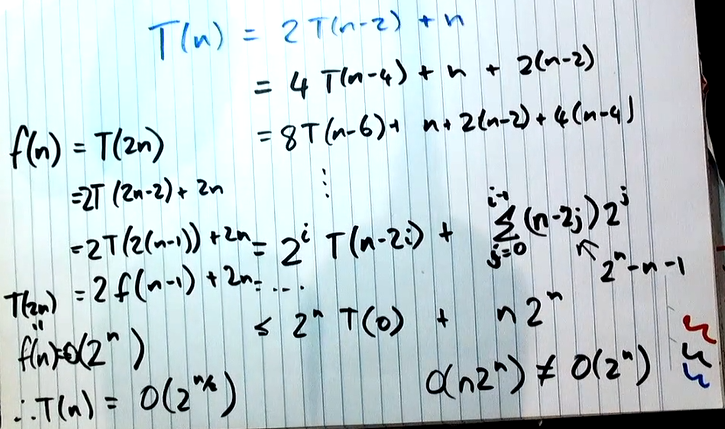
f(n)是另一种简单方法
quiz 8
1. 
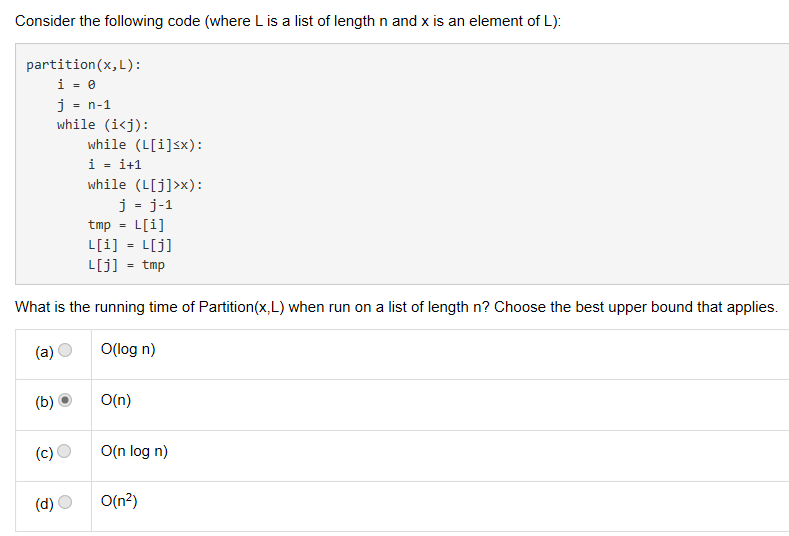
answer: b
2. 
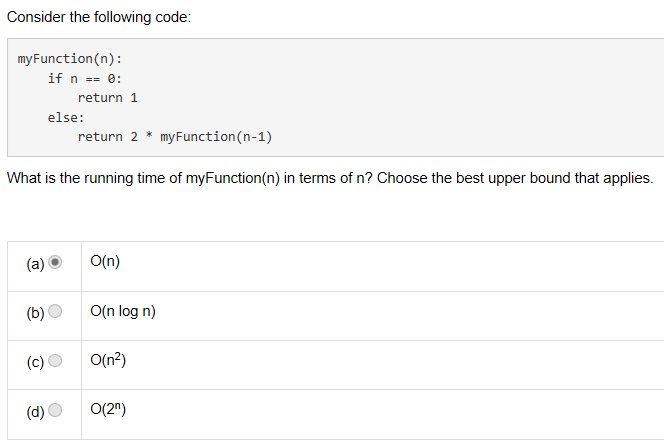
answer: a
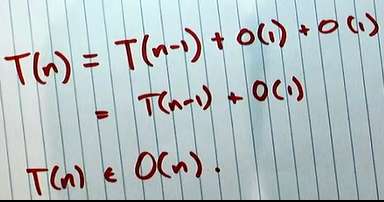
quiz 9
1. 
因为当w属于Σ的闭包时，P(w)成立，所以当a属于Σ时，P(a)成立
因为w属于Σ的闭包，a属于Σ且P(w)成立，即P(aw)相当于在w的基础上加上一个元素，且这个元素仍属于Σ，故而aw恒为Σ的闭包，所以第二个成立
因为P(w)成立，ab同上面一样均属于Σ，故而成立
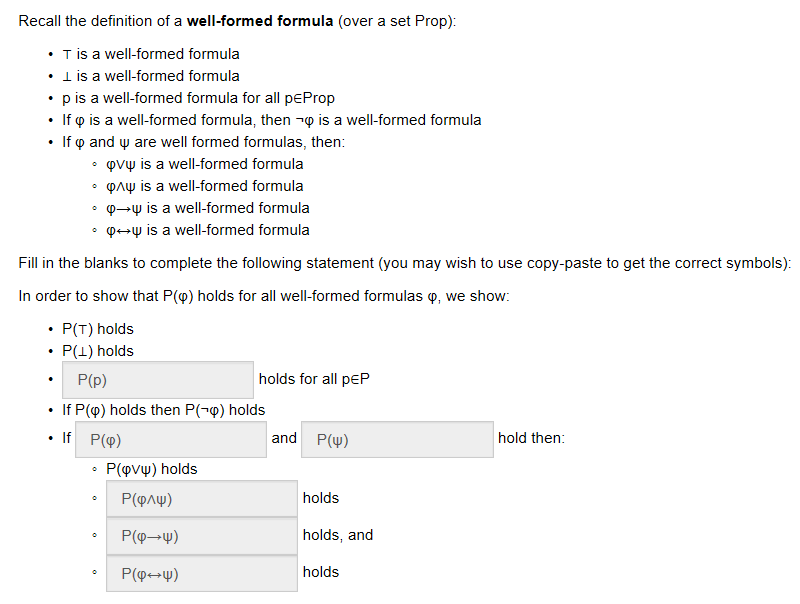
2. 
quiz 10
1. 
answer: acd
b没有()
e中非T外面不需要()
2. 
answer: e
计算出来的结果为flip(φ) = ((¬p∧¬¬q)∨⊤)，¬¬q与q不一样（只是逻辑相同，类比rabbit，bunny）
3. 
answer：a
可以把括号打开，再根据TF判断
quiz 11
1. 
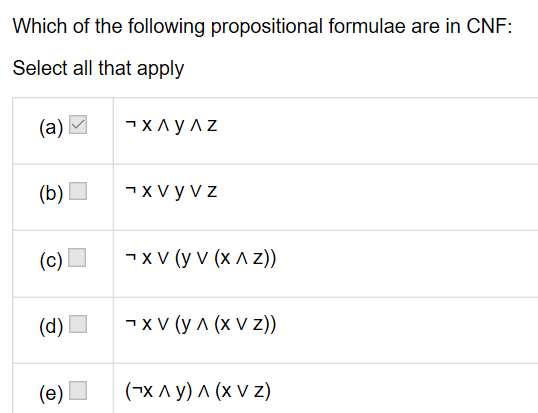
answer: abe
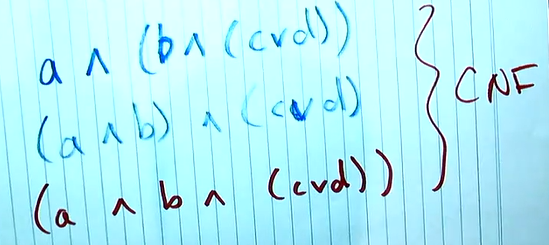
2. 
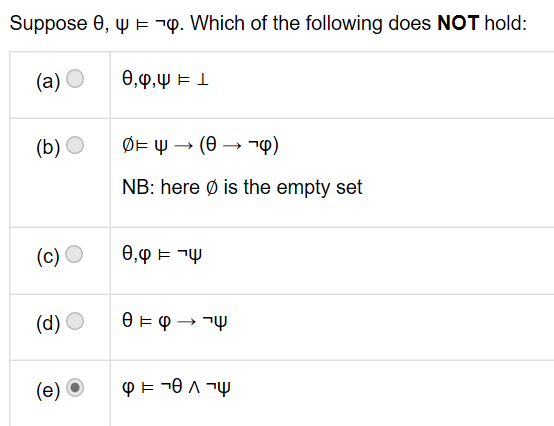
answer: e
3. How many binary boolean functions are there?
answer: 16
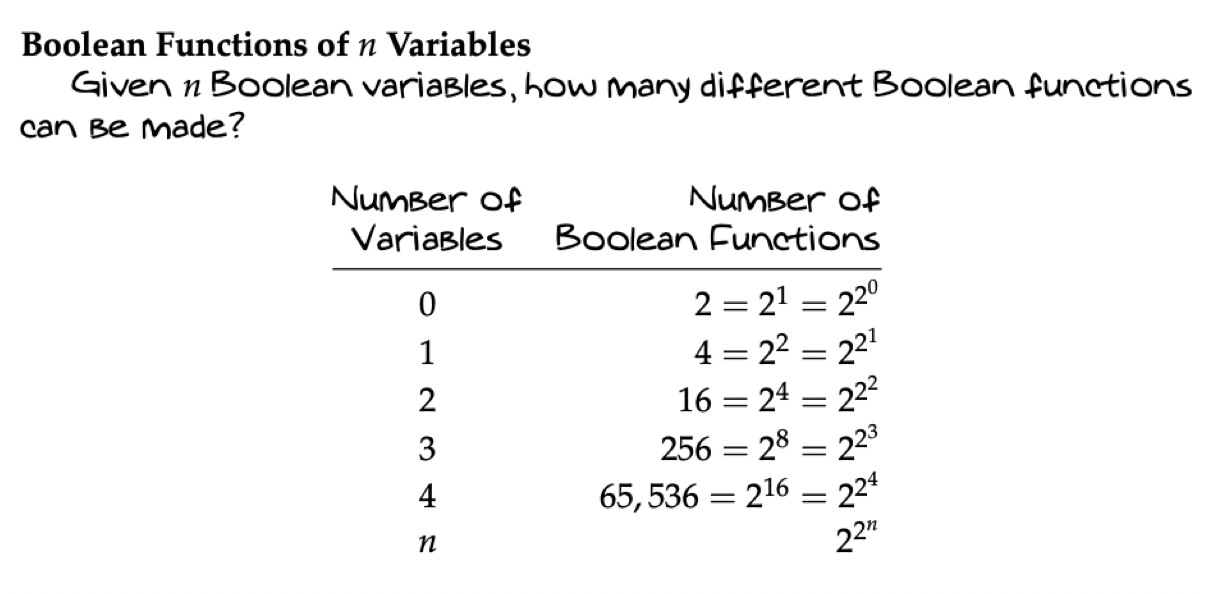
4. 
answer: a
quiz 12
1. 
answer：4
x y z
1 0 0
0 1 0
0 0 1
1 1 1
2. 
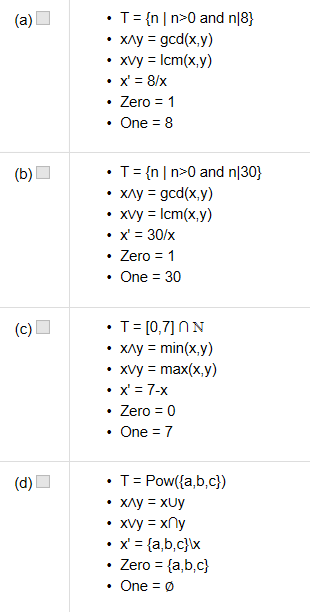
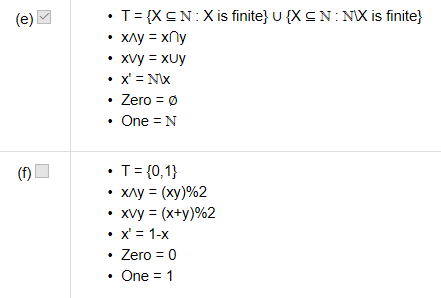
answer: b d e
以a为例，当x为2时，x'=4,x∧x'=2, 而根据identity，应该为Zero=1，所以不对
quiz 13
1. 
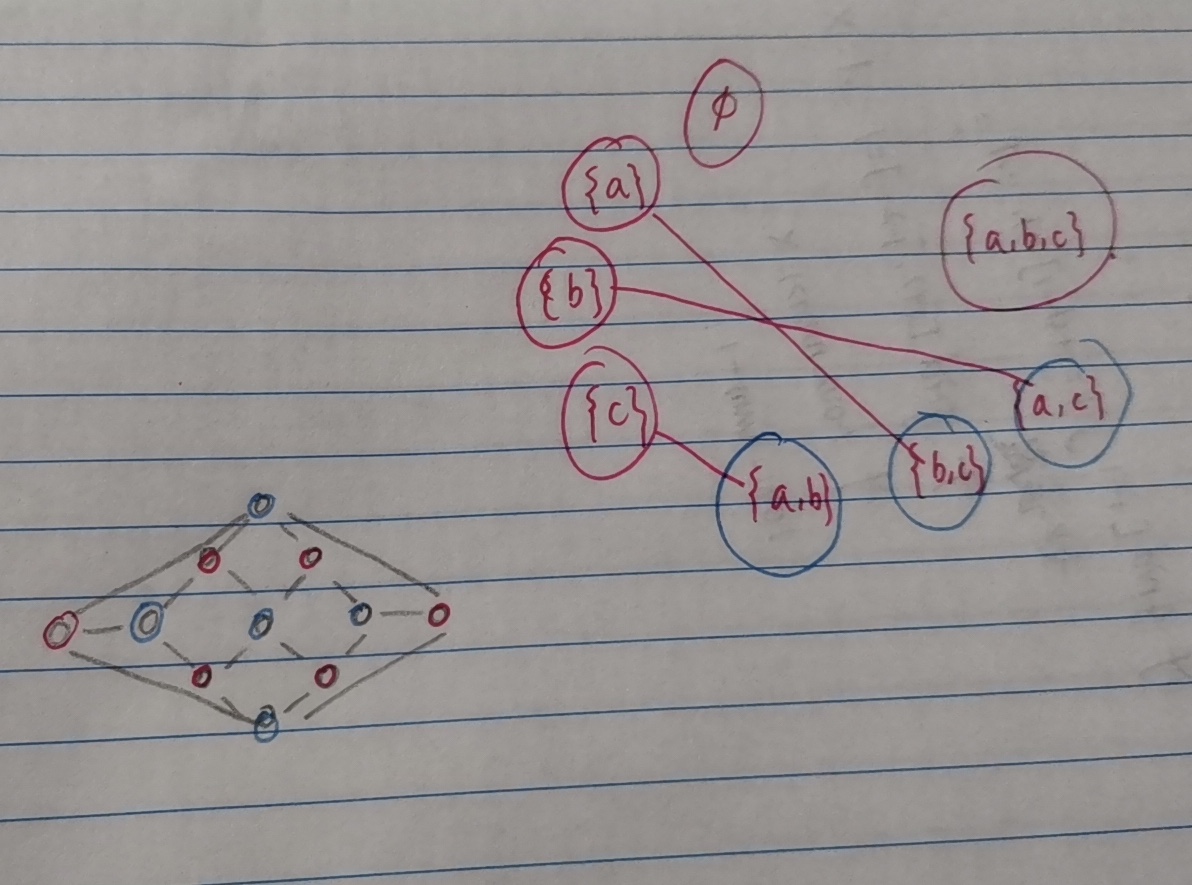
quiz 14
