number theory

read Sec. 1.1-1.3; Sec.3.5

1. natural numbers自然数 N：{0，1，2. . .}

integers整数 Z：{. . .-1，0，1，2. . .}

positive integers：正整数，不包含0

rational numbers(fractions)有理数 Q={m/n : m,n 均为整数}

real numbers(decimal小数 or binary expansions)实数 R

2. floor and ceiling

 

 

 

 

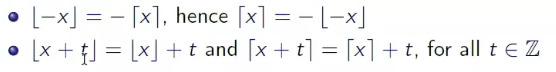
3. 上课没听懂的部分

 

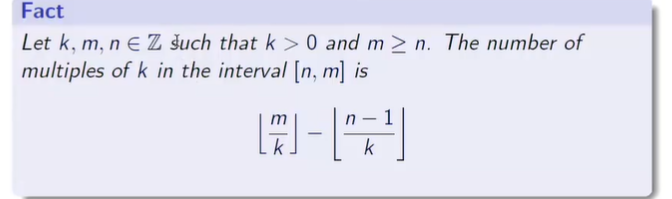
 4. divides表述的是一种关系，所以可以出现0，表述为m | n

5. the greatest common divisor of m and n, gcd(m,n) is the largest positive d such that d|m and d|n最大公约数

the least common multiple of m and n, lcm(m,n), is the smallest positive k such that m|k and n|k最小公倍数

两个数永远为正数

6. 若m,n除1外没有其他公约数，则m,n为relatively prime

7. m,n为正数时，gcd(m,n) * lcm(m,n)=|m| * |n|

8. gcd(0,n) = n

9. 

 

 

 10. mod and div

 

 

mod means ignoring this part

div take the floor, that is why -42 div 9 = -5

11. m = p(mod n) if and only if (m%n) = (p%n)

 if m = m'(mod n) and p = p'(mod n) then:

　　m+p = m'+p'(mod n) and

　　m*p = m'*p'(mod n)

12. 辗转相除法

 

 13.