HDOJ 2071-2080
2071Max Num
Problem Description
There are some students in a class, Can you help teacher find the highest student .
Input
There are some cases. The first line contains an integer t, indicate the cases; Each case have an integer n ( 1 ≤ n ≤ 100 ) , followed n students’ height.
Output
For each case output the highest height, the height to two decimal plases;
Sample Input
2
3 170.00 165.00 180.00
4 165.00 182.00 172.00 160.00
Sample Output
180.00
182.00
2072单词数
Problem Description
lily的好朋友xiaoou333最近很空,他想了一件没有什么意义的事情,就是统计一篇文章里不同单词的总数。下面你的任务是帮助xiaoou333解决这个问题。
Input
有多组数据,每组一行,每组就是一篇小文章。每篇小文章都是由小写字母和空格组成,没有标点符号,遇到#时表示输入结束。
Output
每组只输出一个整数,其单独成行,该整数代表一篇文章里不同单词的总数。
Sample Input
you are my friend
#
Sample Output
4
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
string c1, c2;
while(getline(cin, c1))
{
if(c1 == "#") break;
istringstream stream(c1);
set<string> str;
while(stream >> c2)
str.insert(c2);
printf("%d\n", str.size());
}
return 0;
}
2073无限的路
Problem Description
甜甜从小就喜欢画图画,最近他买了一支智能画笔,由于刚刚接触,所以甜甜只会用它来画直线,于是他就在平面直角坐标系中画出如下的图形:
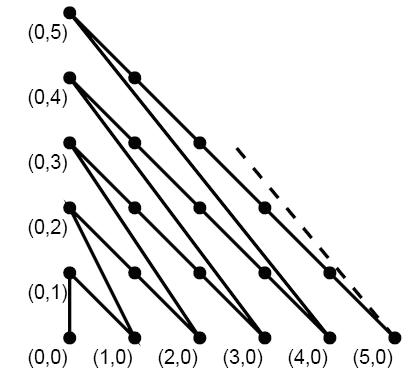
甜甜的好朋友蜜蜜发现上面的图还是有点规则的,于是他问甜甜:在你画的图中,我给你两个点,请你算一算连接两点的折线长度(即沿折线走的路线长度)吧。

甜甜的好朋友蜜蜜发现上面的图还是有点规则的,于是他问甜甜:在你画的图中,我给你两个点,请你算一算连接两点的折线长度(即沿折线走的路线长度)吧。
Input
第一个数是正整数N(≤100)。代表数据的组数。
每组数据由四个非负整数组成x1,y1,x2,y2;所有的数都不会大于100。
每组数据由四个非负整数组成x1,y1,x2,y2;所有的数都不会大于100。
Output
对于每组数据,输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。
Sample Input
5
0 0 0 1
0 0 1 0
2 3 3 1
99 99 9 9
5 5 5 5
Sample Output
1.000
2.414
10.646
54985.047
0.000
图中的路径分为L1:y=-x+k1 和 L2:y=-2x+k2(k1、k2为整数),这两条直线的路径分别为 根号5 和 根号2 的倍数;
要求两点间的距离,就是求 |一点到远点的路径-另一点到原点的路径|
#include <bits/stdc++.h> using namespace std; const double p = sqrt(5); const double q = sqrt(2); double getRoad(double x, double y) { double i; double ans = 1; for (i = 1; i <= x + y; i++) ans += q * i; ans -= q * y; for (i = 0; i <x + y; i++) { ans += sqrt(i * i + (i + 1) * (i + 1)); } return ans; } int main() { double x1, x2, y1, y2; int n; cin >> n; while (n--) { cin >> x1 >> y1 >> x2 >> y2; printf("%.3lf\n", abs(getRoad(x1, y1) - getRoad(x2, y2))); } }
2074叠筐
Problem Description
需要的时候,就把一个个大小差一圈的筐叠上去,使得从上往下看时,边筐花色交错。这个工作现在要让计算机来完成,得看你的了。
Input
输入是一个个的三元组,分别是,外筐尺寸n(n为满足0<n<80的奇整数),中心花色字符,外筐花色字符,后二者都为ASCII可见字符;
Output
输出叠在一起的筐图案,中心花色与外筐花色字符从内层起交错相叠,多筐相叠时,最外筐的角总是被打磨掉。叠筐与叠筐之间应有一行间隔。
Sample Input
11 B A
5 @ W
Sample Output
AAAAAAAAA
ABBBBBBBBBA
ABAAAAAAABA
ABABBBBBABA
ABABAAABABA
ABABABABABA
ABABAAABABA
ABABBBBBABA
ABAAAAAAABA
ABBBBBBBBBA
AAAAAAAAA
@@@
@WWW@
@W@W@
@WWW@
@@@

#include <bits/stdc++.h> using namespace std; char arr[90][90]; int main() { int n; char a, b; int i, j, k; int flag = 1; while (cin >> n >> a >> b) { if (flag == 1) flag = 0; else cout << endl; int x = n / 2 + 1; arr[x][x] = a; int turn = 1; for (i = 1; i < x; i++) { char c; if ((turn + i) % 2 == 1) c = a; else c = b; for (j = x - i; j <= x + i; j++) { arr[x - i][j] = c; arr[x + i][j] = c; arr[j][x - i] = c; arr[j][x + i] = c; } } if (n != 1) { arr[n][1] = ' '; arr[1][n] = ' '; arr[1][1] = ' '; arr[n][n] = ' '; } for (i = 1; i <= n; i++) { for (j = 1; j <= n; j++) cout << arr[i][j]; cout << endl; } } }
2075A|B?
Problem Description
正整数A是否能被正整数B整除,不知道为什么xhd会研究这个问题,来帮帮他吧。
Input
输入数据的第一行是一个数据T,表示有T组数据。
每组数据有两个正整数A和B(A,B<10^9)。
每组数据有两个正整数A和B(A,B<10^9)。
Output
对于每组输入数据,输出"YES"表示可以被整除,"NO"表示不能被整除。
Sample Input
2
4 2
5 3
Sample Output
YES
NO
#include <bits/stdc++.h> using namespace std; int main() { int n; cin >> n; int i; int a, b; while (n--) { cin >> a >> b; if (a % b == 0) cout << "YES" << endl; else cout << "NO" << endl; } }
2076夹角有多大?
Problem Description
时间过的好快,一个学期就这么的过去了,xhd在傻傻的看着表,出于对数据的渴望,突然他想知道这个表的时针和分针的夹角是多少。现在xhd知道的只有时间,请你帮他算出这个夹角。
注:夹角的范围[0,180],时针和分针的转动是连续而不是离散的。
注:夹角的范围[0,180],时针和分针的转动是连续而不是离散的。
Input
输入数据的第一行是一个数据T,表示有T组数据。
每组数据有三个整数h(0 <= h < 24),m(0 <= m < 60),s(0 <= s < 60)分别表示时、分、秒。
每组数据有三个整数h(0 <= h < 24),m(0 <= m < 60),s(0 <= s < 60)分别表示时、分、秒。
Output
对于每组输入数据,输出夹角的大小的整数部分。
Sample Input
2
8 3 17
5 13 30
Sample Output
138
75

不要忘记输入的是24小时制计时法,真的很下头
#include <bits/stdc++.h> using namespace std; int main() { int t; cin >> t; int a, b, c; double tangle1; double tangle2; while (t--) { cin >> a >> b >> c; // 08:03:17 if (a > 12) a -= 12; tangle1 = b * 6 + c * 0.1; tangle2 = a * 30 + 0.5 * b + 0.5 * c / 60; double tangle = abs(tangle2 - tangle1); if (tangle > 180) cout << int(360 - tangle) << endl; else cout << int(tangle) << endl; } }
2077汉诺塔IV
Problem Description
还记得汉诺塔III吗?他的规则是这样的:不允许直接从最左(右)边移到最右(左)边(每次移动一定是移到中间杆或从中间移出),也不允许大盘放到小盘的上面。xhd在想如果我们允许最大的盘子放到最上面会怎么样呢?(只允许最大的放在最上面)当然最后需要的结果是盘子从小到大排在最右边。
Input
输入数据的第一行是一个数据T,表示有T组数据。
每组数据有一个正整数n(1 <= n <= 20),表示有n个盘子。
每组数据有一个正整数n(1 <= n <= 20),表示有n个盘子。
Output
对于每组输入数据,最少需要的摆放次数。
Sample Input
2
1
10
Sample Output
2
19684
2078复习时间
Problem Description
为了能过个好年,xhd开始复习了,于是每天晚上背着书往教室跑。xhd复习有个习惯,在复习完一门课后,他总是挑一门更简单的课进行复习,而他复习这门课的效率为两门课的难度差的平方,而复习第一门课的效率为100和这门课的难度差的平方。xhd这学期选了n门课,但是一晚上他最多只能复习m门课,请问他一晚上复习的最高效率值是多少?
Input
输入数据的第一行是一个数据T,表示有T组数据。
每组数据的第一行是两个整数n(1 <= n <= 40),m(1 <= m <= n)。
接着有n行,每行有一个正整数a(1 <= a <= 100),表示这门课的难度值。
每组数据的第一行是两个整数n(1 <= n <= 40),m(1 <= m <= n)。
接着有n行,每行有一个正整数a(1 <= a <= 100),表示这门课的难度值。
Output
对于每组输入数据,输出一个整数,表示最高效率值。
Sample Input
2
2 2
52
25
12 5
89
64
6
43
56
72
92
23
20
22
37
31
Sample Output
5625
8836
2080夹角有多大II
1°=π/180°,1rad=180°/π
反三角函数算出来的是弧度,要用第二个公式换成角度
#include <bits/stdc++.h> using namespace std; #define PI 3.1415926; int main() { int n; cin >> n; double x1, y1; double x2, y2; for (int i = 0; i < n; i++) { cin >> x1 >> y1 >> x2 >> y2; double tangle1 = atan(y1 / x1) ; double tangle2 = atan(y2 / x2); double tangle = abs(tangle1 - tangle2); if (tangle > 180) tangle=360-tangle; printf("%.2lf\n", tangle*180/3.1415926); } }
atan的范围是-90~90,没办法用
用向量的夹角公式
int main() { int u; double x1,x2,y1,y2; double ans; scanf ("%d",&u); while (u--) { scanf ("%lf %lf %lf %lf",&x1,&y1,&x2,&y2); ans = (x1 * x2 + y1 * y2) / (sqrt(x1*x1+y1*y1) * sqrt(x2*x2 + y2*y2)); ans = acos(ans) * 180 / PI; printf ("%.2lf\n",ans); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号