Logistic Regression

logistic regression用于二分类的情况。即Y∈{0,1}。

 

模型

对于分布形式如下的样本：

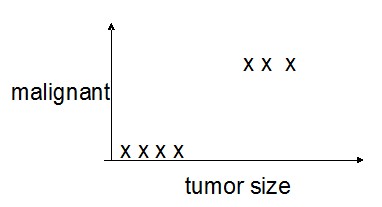
如果使用linear regression的话，可以拟合出一条类似下图的曲线：

通过增加一个阈值，我们也可以做二分类，例如，假定阈值为0.5：

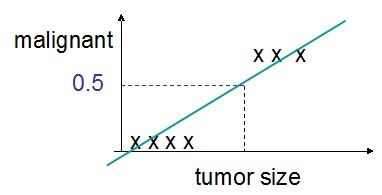
那么，可以写成：

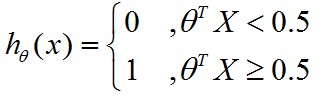
但是这种方式在面对类似这样的数据分布时，会有问题：

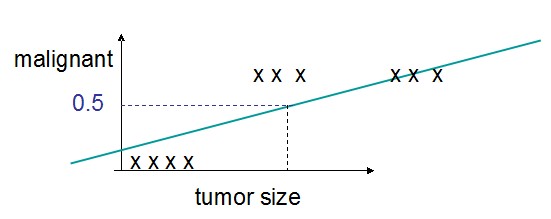
图中的回归线为了拟合到右边的3个奇异点而变得非常斜，这不是我们希望看到的。

为此，我们为logistic regression另外提出了一种模型：

linear regression的计算模型是：h_θ(x)=θ^Tx

logistic regression的计算模型是：h_θ(x)=g(θ^Tx)

注意：我们增加了一个g(z)函数，其中z=θ^Tx

g(z)函数表示一个数据从0到1的分布，使得y∈(0,1)

一般的，我们取

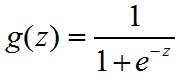
g(z)的图像为：

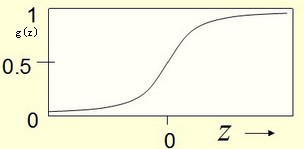
这里函数被称为sigmod函数，也称logistic函数。为什么要选择这样的函数，可以看 @老师木 写的【为什么我们喜欢用sigmoid这类S型非线性变换？】。

现在，我们的h_θ(x)就变为了

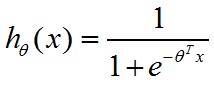
其中，θ为参数。h_θ(x)∈[0,1]

 

惩罚函数 cost function

要对监督型模型进行训练，我们就需要一个cost函数来做penalty。在linear regression中，我们使用error square来做cost。但在现在模型下，如果使用error square的话，会使cost 函数变成一个非凸函数（non-convex），这样不容易进行optimization。

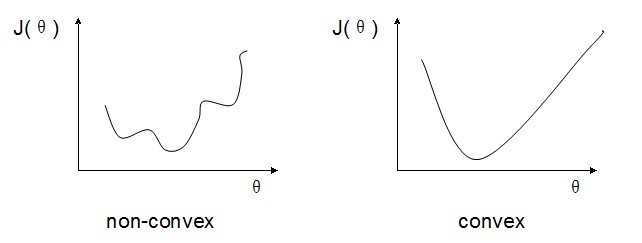
现在，我们假设只有一个样本，且y=1.

如果使用error square的方式的话，则有