2020软工个人项目作业-平面几何图形交点统计

2020软工个人项目作业-平面几何图形交点统计

项目	内容
课程链接	2020春季计算机学院软件工程(罗杰 任健)
作业要求	个人项目作业
课程目标	系统学习软件开发理论和流程，通过实践积累软件开发经验
本博客的收获	熟悉了C++语法，熟悉了VS工具使用，将书中开发项目的流程简单实践
教学班级	005
项目地址	https://github.com/eitbar/IntersectProject.git

一、估计将在程序的各个模块的开发上耗费的时间

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	60
· Design Spec	· 生成设计文档	40	100
· Design Review	· 设计复审 (和同事审核设计文档)	10	50
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	0	0
· Design	· 具体设计	60	60
· Coding	· 具体编码	150	150
· Code Review	· 代码复审	10	20
· Test	· 测试（自我测试，修改代码，提交修改）	60	120
Reporting	报告
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	120
	合计	580	730

从上表看出，设计阶段、测试阶段以及总结阶段与预估时间相差较大。

我将思考解题算法以及代码设计归入生成设计文档，和同学讨论该怎么做归入设计复审。事后感觉这两部分并不应该花这么长时间，太过担心性能而举棋不定、犹犹豫豫不是什么好事，而且从最终结果来看，纠结了半天使用的还是简单的“暴力”，这两部分时间是被“浪费”掉的。

测试阶段是因为在不熟悉单元测试的情况下错误测试花费时间，以及研究性能提升的方法也花费了较长时间。

二、解题思路描述

需求分析

功能需求：给定 N 条直线，询问平面中有多少个点在至少 2 条给定的直线上。题目输入保证答案只有有限个。

测试需求：提交的程序需要支持传入参数及相应约定。

附加拓展需求：图形中有圆。

用不严谨的通俗语言描述，问题即平面上N个直线共有几个不重复的交点。需要注意的有以下几点：

• 多条直线可能交于一点。
• 直线的信息由两个整数坐标点确定，但交点坐标可能为小数。
• 项目要求能支持命令行参数，数据文件读取，输出写入文件。
• 总的交点个数小于5000000，意味着可能会有大量的重复点计算。
• N可能会很大。

需要掌握的知识：直线与圆的表示。直线与直线求交点的计算方法。圆与圆的求交点的计算方法。圆与直线的求交点的方法。

解题思路

最直接的一个想法，就是N条直线两两计算交点坐标并保存，不重复保存相同的坐标，最终统计保存的坐标的个数即为题目答案。使用Hash判重，假定时间复杂度为计算常数O(k)，那么该做法时间复杂度为O(N²*k)，空间复杂度为O(N²)。组略估算O(10⁸)为1秒的话，且加上计算常数的话，当N小于等于1000时，该做法可以在60秒内得到结果，满足正确性评分的需求，但考虑到性能部分的要求，该方法需要被改进。

进一步思考，平行线之间肯定无交点，那么遍历的时候是否可以忽略平行线呢？我们可以通过计算每条直线的斜率，来给直线分组，斜率相同的直线为一组，同组间直线无需遍历。假如最后共分 \(m\) 组，每组 \(l_i\) 条直线，因此总共会减少 \(\sum l_i^2\) 次计算，在某些情况下，性能应该可以有一定的提升，但仍然无法保证肯定在60s内得到结果。

再仔细想想，算法的瓶颈主要在于重复点的计算，是否可以通过某种方法减少重复点的计算呢？我们将N条直线按顺序添加到整个图中，在计算交点时，记录下该交点被多少条直线相交。但是由于C++使用经验比较匮乏，而且不好估算计算交点的时间复杂度与C++标准库中一些数据结构的使用时间复杂度，因此作罢。

最后考虑到拓展需求圆的话，可以先用上述方法处理完直线，再直接暴力处理圆。

我到网络上查询了相关问题，可是并没有获得好的算法，希望作业结束后，能从老师以及其他同学博客中获得新的知识。

三、设计实现过程

首先，需要存储输入的几何图形的信息，即直线类、圆类，类中可以提前存储之后需要计算的部分以节省时间。接着在我们的算法中，还需要为几何图形的交点构建交点类。

三个类的具体设计为：

• 交点类：

  • 属性：double：横坐标；
  • 属性：double：纵坐标；

• 直线类：

  • 属性：double,double,double：直线一般方程的三个参数(\(ax+by+c=0\))；
  • 属性：double,double：斜率(斜率为正无穷时，规定为inf)，截距(为正无穷时，规定为inf)；
  • 属性：double,double：直线过的任意一点；
  • 方法：Point：求与另一条直线的交点

• 圆类：

  • 属性：double,double：圆心坐标；
  • 属性：double：半径；
  • 属性：double,double,double：圆的一般方程的三个参数(\(x^2+y^2+dx+ey+f=0\))
  • 方法：std::vector<Point>：求与另一条直线的交点
  • 方法：std::vector<Point>：求与另一个圆的交点

交点使用map、set等可以快速查询的数据结构进行存储。直线使用数组、set等可以组织顺序的数据结构存储。圆使用任意可以遍历的数据结构存储。

主函数的处理流程为，读取命令行参数，简单解析后，读取数据，并保存在数组或其他数据结构中。接着将问题拆分为直线与直线的交点，圆与其他几何图形的交点。调用solveLine()函数统计直线与直线交点个数，再调用solveCycle()函数统计圆与直线的交点个数。最后输出结果到文件中。

solveLine()函数的主要流程为：首先，将直线按照斜率分组，默认开始处理前平面上没有任何几何图形。接着依次向平面中添加直线，添加时调用该直线求与直线交点的函数，计算直线与平面中已有直线的交点，查询交点是否已经存在，若不存在，将交点存入数据结构，并且统计数量增加。

solveCycle()函数的主要流程为：依次向平面中添加圆，并调用该圆求与其他几何图形交点的函数，计算与已有图形的交点，查询交点是否已经存在，若不存在，将交点存入数据结构，并且统计数量增加。

直线与直线的交点计算函数：先判断是否平行，若平行返回特殊点，否则，使用计算公式计算交点。此处需要设置单元测试，测试计算结果是否正确。测试平行情况下、斜率为0、斜率不存在的直线互相相交的情况。

圆与直线的交点计算函数：先计算直线与圆心距离，判断有几个交点，若没有交点，返回空队列；若相切一个交点则计算圆心向直线作垂线的垂足，并返回包含一个交点的队列；若有两个交点，先计算圆心向直线作垂线的垂足，再沿直线的方向向量加减一定的长度，得到两个交点，并返回包含两个交点的队列。此处需要设置单元测试，测试计算结果是否正确。测试圆与直线相切、相交、相离的求交点情况，其中直线需要包括斜率为0、斜率不存在的特殊情况。

圆与圆的交点计算函数：先通过圆心距离判断两圆是否相交，若不相交则返回空队列；若相交则通过圆的一般方程计算出直线，再计算圆与直线的交点个数。此处需要设置单元测试，测试圆与圆内切、外切、相交、外离、内含的求交点情况。

除了必要函数之外，需要新增浮点数比较函数，精度设置为1e-8。该函数接受两个参数，若第一个参数大于第二个，则返回正数，等于返回0，小于返回负数。此处需要设置单元测试，测试浮点数比较是否正确。

如果使用的数据结构需要对类型重载，也需要编写相应的重载函数。

四、性能改进。

初版程序性能分析

在完成初版代码，反复修改bug，并通过单元测试和一系列数据测试之后，对程序进行性能分析。

性能分析使用数据为：随机生成的7000条几何图形数据，其中直线与圆各3500个，最终计算得到交点数为22191950个交点。随机数生成模块为python中random包。生成数据所用代码以及性能测试时使用的数据已经上传至github项目中。

VS2019中使用性能探查器，分析CPU利用率如下：

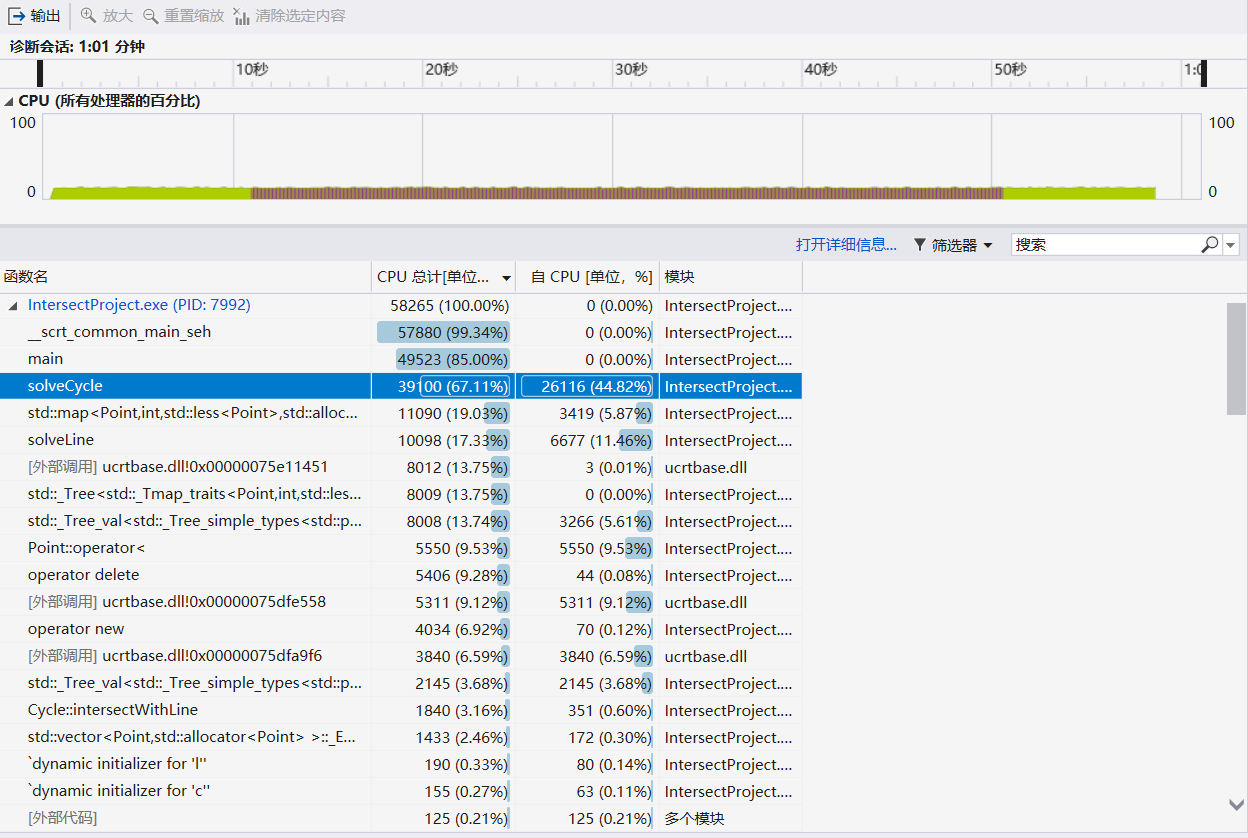
可以看出，耗费时间最多的函数，应该是统计所有的圆与其他几何图形的交点的函数，这也在情理之中。点进详细报告页面，分析solveCycle()函数结果如下：

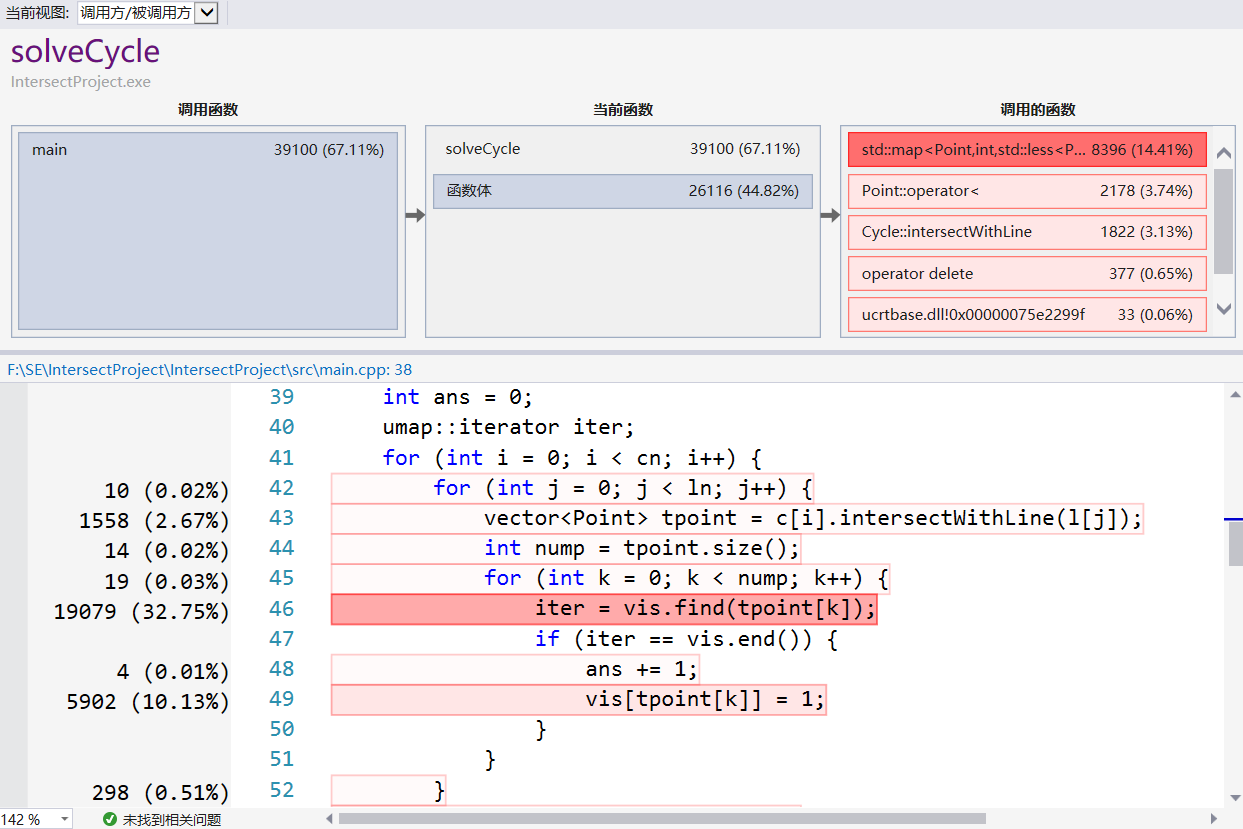
令人意外的是，相比计算所占时间，在圆与直线求交点的过程中，对map数据结构的修改与查询花费的时间更多。通过查阅资料可知，C++标准库中map主要通过红黑树实现，查询和修改时间复杂度均为\(O(\log(n))\)。然而，在本题中，我们完全不需要用到其顺序结构，而且Point类内容较为简单。经过一番资料查询，我发现C++中有unordered_map这一数据结构，其功能类似java中hashmap，在查询和修改方面速度快于map，因此我决定更换记录交点的数据结构为unordered_map，并为Point重载hash方法。

初步优化后性能分析

将记录交点的数据结构更换为unordered_map后，我是用同样的数据、同样的操作对程序进行性能分析，得到结果如下：

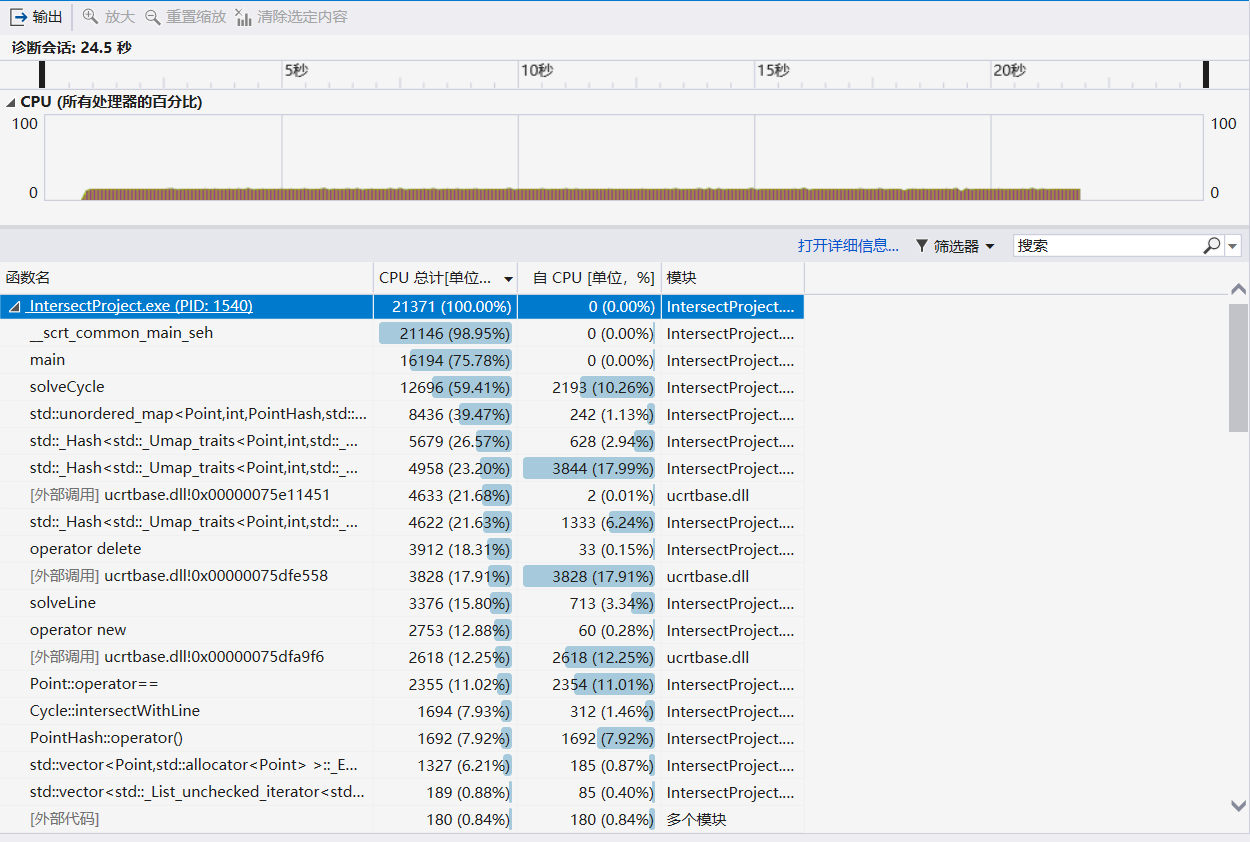
可以从整个程序的运行时间上，明显的感受到更换数据结构带来的优化。从原本的1分01秒降低到了24.5秒，值得开心一小会儿 😃

但是，转念感觉到有些奇怪，本以为程序的性能瓶颈应该是多次重复计算交点，但为什么此处变成了记录交点的数据结构的使用呢？

性能优化后续思考

随后，通过分析测试性能用的数据，我发现我的测试数据其实是与需求不符的数据，因此该性能分析其实并不能帮我解决算法的瓶颈在何处。

因为我使用的数据是随机生成的，重合的交点很少，总的交点数很多，因此时间复杂度被堆在了维护交点的数据结构上。而题目明确说明，交点有个数限制，针对题目的需求，性能优化的重点其实应该放在减少重复点的计算上，这个数据结构的改动可能在实际测试中只能占小头。

不合理的测试数据，帮我得出了不合理的性能瓶颈，因此该性能分析其实并不能帮我解决算法的瓶颈在何处，更改这个数据结构最终能帮到我的应该也不会很多。

除了如何生成更合理的测试数据外，还有一个问题让我略感疑惑。在实际软件开发中，性能优化应该是必不可少的一环，当我们软件还没成型的时候，没有用户数据，如何知道哪里才是性能优化的重点呢？如果侧重点出错，比如我花大力气去自己写一个插入查找速度极快的数据结构（我就可以直接发论文作报告走上人生巅峰了），结果在实际使用中别人根本不去使用这个功能，或者说这个功能的速度其实并不影响客户的体验，那我是不是白费力气了呢？

五、关键代码说明

首先，使用vs2019自带的类图查看器生成的类图如下：

自认为我的关键代码有三部分。

• solveLine()：往平面中添加直线计算交点并忽略平行线，这部分应该是我与直接暴力求交点唯一不同的部分啦，而且按交点个数较少来推论，平行线应该不多，优化的性能不值一提。代码及注释如下图所示：

  int solveLine() {
  	//ans为统计交点个数
  	int ans = 0;
  	//将直线按斜率排序，实现斜率分组功能
  	sort(l, l + ln);
  	//map查找用的迭代器
  	umap::iterator iter;
  	//依次遍历直线，当前待添加直线为i
  	for (int i = 0; i < ln; i++) {
  		//按顺序遍历已经添加到平面中的直线
  		for (int j = 0; j < i; j++) {
  			//如果遍历到平面中直线j与i的斜率相同，那么j~i之间的直线斜率都与i相同，不再计算i
  			if (doublecompare(l[i].k, l[j].k) == 0) {
  				break;
  			}
  			//求直线i与j的交点
  			Point tpoint = l[i].intersectWithLine(l[j]);
  			//如果是新交点，加入umap中，并统计结果，否则不做处理
  			iter = vis.find(tpoint);
  			if (iter == vis.end()) {
  				ans += 1;
  				vis[tpoint] = 1;
  			}
  		}
  	}
  	return ans;
  }
  

• std::vector<Point> Cycle::intersectWithLine(Line t)：求圆与直线的交点，并保存在vector中返回，思路为先求垂足，再沿方向向量加减，代码及注释如下：

  std::vector<Point> Cycle::intersectWithLine(Line t) {
  	//交点vector
  	std::vector<Point>ps;
  	//先计算圆心到直线的距离
  	double ld = abs(t.a * x + t.b * y + t.c) / sqrt(t.a * t.a + t.b * t.b);
  	//相离
  	if (doublecompare(ld, r) == 1) {
  		return ps;
  	}
  	//相切
  	else if (doublecompare(ld, r) == 0) {
  		//斜率不存在，横坐标为直线横坐标，纵坐标为圆心纵坐标
  		if (t.k == inf_k) {
  			ps.push_back(Point(t.x1, y));
  			return ps;
  		}
  		//斜率为0，横坐标为圆心横坐标，纵坐标为直线纵坐标
  		if (t.k == 0) {
  			ps.push_back(Point(x, t.y1));
  			return ps;
  		}
  		//斜率正常
  		//先算过圆心与直线t垂直的线y=-1/k*x+b2
  		double b2 = x / t.k + y;
  		//直线t斜截式中b1
  		double b1 = t.b1;
  		//两直线求交点，即垂足
  		double xt = t.k * (b2 - b1) / (1 + t.k * t.k);
  		double yt = t.k * xt + b1;
  		//相切时，垂足即交点
  		ps.push_back(Point(xt, yt));
  		return ps;
  	}
  	//相交
  	double ln = sqrt(r * r - ld * ld);
  	//同理
  	if (t.k == inf_k) {
  		ps.push_back(Point(t.x1, y - ln));
  		ps.push_back(Point(t.x1, y + ln));
  		return ps;
  	}
  	if (t.k == 0) {
  		ps.push_back(Point(x - ln, t.y1));
  		ps.push_back(Point(x + ln, t.y1));
  		return ps;
  	}
  	double b2 = x / t.k + y;
  	double b1 = t.b1;
  	double xt = t.k * (b2 - b1) / (1 + t.k * t.k);
  	double yt = t.k * xt + b1;
  	//求出垂足后，求直线方向向量
  	double s1k2 = sqrt(1 + t.k * t.k);
  	double nx = 1 / s1k2;
  	double ny = t.k / s1k2;
  	//加减方向向量与半弦长的乘积得到两个交点
  	ps.push_back(Point(xt + ln * nx, yt + ln * ny));
  	ps.push_back(Point(xt - ln * nx, yt - ln * ny));
  	return ps;
  }
  

• std::size_t operator()(const Point& c) const：使用unordered_map时为Point类指定的hash函数，代码如下：

  class PointHash
  {
  public:
  	std::size_t operator()(const Point& c) const
  	{
  		//直接利用库中hash函数，为防止32/64位操作系统的影响，默认size_t为32位，x,y各分16位
  		return hash<double>()(c.x) + (hash<double>()(c.y) << 16);
  	}
  };
  

六、代码警告消除

使用VS2019本机推荐规则，错误数和警告数都为0！