基于单层决策树的AdaBoost算法原理+python实现
这里整理一下实验课实现的基于单层决策树的弱分类器的AdaBoost算法。
由于是初学,实验课在找资料的时候看到别人的代码中有太多英文的缩写,不容易看懂,而且还要同时看代码实现的细节、算法的原理什么的,就体验很不好。
于是我这里代码中英文没有用缩写,也尽量把思路写清楚。
基本概念
-
集成学习:通过组合多个基分类器(base classifier)来完成学习任务,基分类器一般采用弱学习器。
-
弱学习器:只学习正确率仅仅略优于随机猜测的学习器。通过集成方法,就能组合成一个强学习器。
-
Bagging和Boosting:集成学习主要的两种把弱分类器组装成强分类器的方法。
-
AdaBoost是adaptive boosting的缩写。
-
Bagging:从原始数据集中有放回地抽训练集,每轮训练集之间是独立的。每次使用一个训练集得到一个模型。分类问题就让这些模型投票得到分类结果,回归问题就算这些模型的均值。
-
Boosting:每一轮的训练集不变,只是训练集中每个样本在分类器中的权重发生变化,并且每一轮的样本的权重分布依赖上一轮的分类结果。每个弱分类器也都有各自的权重,分类误差小的分类器有更大的权重。
-
举个例子:Bagging+决策树=随机森林;Boosting+决策树=提升树
-
AdaBoost:计算样本权重->计算错误率->计算弱学习器的权重->更新样本权重...重复。
原理+代码实现
就是构造弱分类器,再根据一定方法组装起来。
from numpy import *
加载数据集
用的是实验课给的数据集(horseColic 马疝病数据集)...这部分不多说了。带_array后缀的是列表,带_matrix后缀的是把相应array变成的np矩阵。
def load_dataset(filename):
num_feature = len(open(filename).readline().split('\t'))
data_array = []
label_array = []
f = open(filename)
for line in f.readlines():
line_array = []
current_line = line.strip().split('\t')
for i in range(num_feature - 1):
line_array.append(float(current_line[i]))
data_array.append(line_array)
label_array.append(float(current_line[-1]))
return data_array, label_array
基于单层决策树构建弱分类器
1、废话文学一下,stump的意思是树桩,单层决策树就是只有一层的决策树,就是简单的通过大于和小于根据阈值(threshold)把数据分为两堆。在阈值一边的数据被分到类别-1,另一边分到类别1。
def stump_classify(data_matrix, dimension, threshold, inequality_sign):
# dimension是数据集第dimension维的特征,对应data_matrix的第dimension列
return_array = ones((shape(data_matrix)[0], 1))
if inequality_sign == 'less_than':
return_array[data_matrix[:, dimension] <= threshold] = -1.0
else:
return_array[data_matrix[:, dimension] > threshold] = -1.0
return return_array
2、遍历上面stump_classify函数所有可能的输入值,找到最佳的单层决策树(给定权重向量d时所得到的最佳单层决策树)。best_stump就是最佳的单层决策树,一个字典,里面存放这个单层决策树的'dimension'(上一段代码注释)、'threshold'(阈值)、'inequality_sign'(不等号,less_than和greater_than)。
结合代码和注释看即可。
def build_stump(data_array, class_labels, d):
data_matrix = mat(data_array)
label_matrix = mat(class_labels).T
m, n = shape(data_matrix)
num_steps = 10.0
best_stump = {} # 用于存放给定权重向量d时所得到的最佳单层决策树的相关信息
best_class_estimate = mat(zeros((m, 1)))
'''
将最小错误率min_error设为inf
对数据集中的每一个特征(第一层循环):
对每一个步长(第二层循环):
对每一个不等号(第三层循环):
建立一棵单层决策树并利用加权数据集对它进行测试
如果错误率低于min_error,则将当前单层决策树设为最佳单层决策树
返回最佳单层决策树
'''
min_error = inf
for i in range(n):
range_min = data_matrix[:, i].min()
range_max = data_matrix[:, i].max()
step_size = (range_max - range_min) / num_steps
for j in range(-1, int(num_steps) + 1):
for inequality_sign in ['less_than', 'greater_than']:
threshold = (range_min + float(j) * step_size)
predicted_values = stump_classify(data_matrix, i, threshold, inequality_sign) # 调用stump_classify函数来得到预测结果
error_array = mat(ones((m, 1))) # 这是一个与分类预测结果相同长度的列向量,如果predicted_values中的值不等于label_matrix中的标签值,对应位置就为1,否则为0.
error_array[predicted_values == label_matrix] = 0
weighted_error = d.T * error_array # 这个是加权错误率,这个将用来更新权重向量d
if weighted_error < min_error:
min_error = weighted_error
best_class_estimate = predicted_values.copy()
best_stump['dimension'] = i
best_stump['threshold'] = threshold
best_stump['inequality_sign'] = inequality_sign
return best_stump, min_error, best_class_estimate
加权错误率weighted_error是与AdaBoost交互的地方,每次用于更新权重向量d.
Adaboost的训练过程和分类
训练
训练出来的返回值是: weak_classifier_array, aggregate_class_estimate,一个存放了很多弱分类器的数组和集成学习的类别估计值。
于是思路是,对于每次迭代:利用build_stump找到最佳的单层决策树;把这个最佳单层决策树放进弱分类器数组;利用错误率计算弱分类器的权重α;更新权重向量d;更新集成学习的类别估计值;更新错误率。
里面出现的公式:
-
错误率:

-
利用错误率计算弱分类器的权重α:
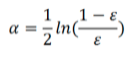
可见错误率ε越高,这个分类器的权重就越小。代码中:
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16])))
(注:max函数里面加中括号是因为之前from numpy import *了,这个max是np.amax,不加中括号会有一个warning.)
- 更新权重向量d:就是使被分错的样本在接下来学习中可以重点对其进行学习。
第i个样本分类正确就是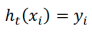
,Zt是sum(D)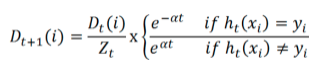
上面公式浅看一下,编程是对着化简合并后的公式来的:
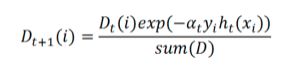
代码中:
exp的指数:exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate)
d:d = multiply(d, exp(exponent))和d = d / d.sum()
- 集成学习的类别估计值(aggregate_class_estimate)就是把每个弱分类器给出的估计值按照每个弱分类器的权重累加起来。代码中是在一个循环里:
aggregate_class_estimate += alpha * class_estimate
下面直接放代码应该就很清楚了:
def ada_boost_train_decision_stump(data_array, class_labels, num_iteration=40):
weak_classifier_array = []
m = shape(data_array)[0]
d = mat(ones((m, 1)) / m)
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(num_iteration):
best_stump, error, class_estimate = build_stump(data_array, class_labels, d) # 利用build_stump找到最佳单层决策树
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16]))) # 算α
best_stump['alpha'] = alpha
weak_classifier_array.append(best_stump) # 把这个最佳单层决策树扔进弱分类器数组
exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate) # 算d
d = multiply(d, exp(exponent))
d = d / d.sum()
aggregate_class_estimate += alpha * class_estimate # 算集成学习的类别估计值
aggregate_errors = multiply(sign(aggregate_class_estimate) != mat(class_labels).T, ones((m, 1)))
error_rate = aggregate_errors.sum() / m
if error_rate == 0.0: # 如果错误率为0了就退出循环
break
return weak_classifier_array, aggregate_class_estimate
分类
就是写个循环,把上面得到的弱分类器数组里面每个弱分类器的放进stump_classify函数里面跑一遍,根据每个的权重把结果累加起来即可。
def ada_boost_classify(data_array, classifier_array):
data_matrix = mat(data_array)
m = shape(data_matrix)[0]
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(len(classifier_array)):
class_estimate = stump_classify(data_matrix,
classifier_array[i]['dimension'],
classifier_array[i]['threshold'],
classifier_array[i]['inequality_sign'])
aggregate_class_estimate += classifier_array[i]['alpha'] * class_estimate
return sign(aggregate_class_estimate)
以上就是实现过程了。下面再放上比较正规的伪代码:

完整代码
from numpy import *
def load_dataset(filename):
num_feature = len(open(filename).readline().split('\t'))
data_array = []
label_array = []
f = open(filename)
for line in f.readlines():
line_array = []
current_line = line.strip().split('\t')
for i in range(num_feature - 1):
line_array.append(float(current_line[i]))
data_array.append(line_array)
label_array.append(float(current_line[-1]))
return data_array, label_array
def stump_classify(data_matrix, dimension, threshold, inequality_sign):
return_array = ones((shape(data_matrix)[0], 1))
if inequality_sign == 'less_than':
return_array[data_matrix[:, dimension] <= threshold] = -1.0
else:
return_array[data_matrix[:, dimension] > threshold] = -1.0
return return_array
def build_stump(data_array, class_labels, d):
data_matrix = mat(data_array)
label_matrix = mat(class_labels).T
m, n = shape(data_matrix)
num_steps = 10.0
best_stump = {}
best_class_estimate = mat(zeros((m, 1)))
min_error = inf
for i in range(n):
range_min = data_matrix[:, i].min()
range_max = data_matrix[:, i].max()
step_size = (range_max - range_min) / num_steps
for j in range(-1, int(num_steps) + 1):
for inequality_sign in ['less_than', 'greater_than']:
threshold = (range_min + float(j) * step_size)
predicted_values = stump_classify(data_matrix, i, threshold, inequality_sign)
error_array = mat(ones((m, 1)))
error_array[predicted_values == label_matrix] = 0
weighted_error = d.T * error_array
if weighted_error < min_error:
min_error = weighted_error
best_class_estimate = predicted_values.copy()
best_stump['dimension'] = i
best_stump['threshold'] = threshold
best_stump['inequality_sign'] = inequality_sign
return best_stump, min_error, best_class_estimate
def ada_boost_train_decision_stump(data_array, class_labels, num_iteration=40):
weak_classifier_array = []
m = shape(data_array)[0]
d = mat(ones((m, 1)) / m)
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(num_iteration):
best_stump, error, class_estimate = build_stump(data_array, class_labels, d)
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16])))
best_stump['alpha'] = alpha
weak_classifier_array.append(best_stump)
exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate)
d = multiply(d, exp(exponent))
d = d / d.sum()
aggregate_class_estimate += alpha * class_estimate
aggregate_errors = multiply(sign(aggregate_class_estimate) != mat(class_labels).T, ones((m, 1)))
error_rate = aggregate_errors.sum() / m
if error_rate == 0.0:
break
return weak_classifier_array, aggregate_class_estimate
def ada_boost_classify(data_array, classifier_array):
data_matrix = mat(data_array)
m = shape(data_matrix)[0]
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(len(classifier_array)):
class_estimate = stump_classify(data_matrix,
classifier_array[i]['dimension'],
classifier_array[i]['threshold'],
classifier_array[i]['inequality_sign'])
aggregate_class_estimate += classifier_array[i]['alpha'] * class_estimate
return sign(aggregate_class_estimate)
def main():
data_array, label_array = load_dataset('AdaBoost/horseColicTraining2.txt')
weak_classier_array, aggregate_class_estimate = ada_boost_train_decision_stump(data_array, label_array, 40)
test_array, test_label_array = load_dataset('AdaBoost/horseColicTest2.txt')
print(weak_classier_array)
predictions = ada_boost_classify(data_array, weak_classier_array)
error_array = mat(ones((len(data_array), 1)))
print('error rate of training set: %.3f%%'
% float(error_array[predictions != mat(label_array).T].sum() / len(data_array) * 100))
predictions = ada_boost_classify(test_array, weak_classier_array)
error_array = mat(ones((len(test_array), 1)))
print('error rate of test set: %.3f%%'
% float(error_array[predictions != mat(test_label_array).T].sum() / len(test_array) * 100))
if __name__ == '__main__':
main()
输出是:前面是训练得到的弱分类器,后面是错误率。
[{'dimension': 9, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.4616623792657674}, {'dimension': 17, 'threshold': 52.5, 'inequality_sign': 'greater_than', 'alpha': 0.31248245042467104}, {'dimension': 3, 'threshold': 55.199999999999996, 'inequality_sign': 'greater_than', 'alpha': 0.2868097320169572}, {'dimension': 18, 'threshold': 62.300000000000004, 'inequality_sign': 'less_than', 'alpha': 0.23297004638939556}, {'dimension': 10, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.19803846151213728}, {'dimension': 5, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.1884788734902058}, {'dimension': 12, 'threshold': 1.2, 'inequality_sign': 'less_than', 'alpha': 0.1522736899747682}, {'dimension': 7, 'threshold': 1.2, 'inequality_sign': 'greater_than', 'alpha': 0.15510870821690584}, {'dimension': 5, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.1353619735335944}, {'dimension': 4, 'threshold': 28.799999999999997, 'inequality_sign': 'less_than', 'alpha': 0.12521587326132164}, {'dimension': 11, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.13347648128207715}, {'dimension': 9, 'threshold': 4.0, 'inequality_sign': 'less_than', 'alpha': 0.14182243253771004}, {'dimension': 14, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.10264268449708018}, {'dimension': 0, 'threshold': 1.0, 'inequality_sign': 'less_than', 'alpha': 0.11883732872109554}, {'dimension': 4, 'threshold': 19.2, 'inequality_sign': 'greater_than', 'alpha': 0.09879216527106725}, {'dimension': 2, 'threshold': 36.72, 'inequality_sign': 'less_than', 'alpha': 0.12029960885056902}, {'dimension': 3, 'threshold': 92.0, 'inequality_sign': 'less_than', 'alpha': 0.10846927663989149}, {'dimension': 15, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.09652967982091365}, {'dimension': 3, 'threshold': 73.6, 'inequality_sign': 'greater_than', 'alpha': 0.08958515309272022}, {'dimension': 18, 'threshold': 8.9, 'inequality_sign': 'less_than', 'alpha': 0.0921036196127237}, {'dimension': 16, 'threshold': 4.0, 'inequality_sign': 'greater_than', 'alpha': 0.10464142217079568}, {'dimension': 11, 'threshold': 3.2, 'inequality_sign': 'less_than', 'alpha': 0.09575457291711578}, {'dimension': 20, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.09624217440331542}, {'dimension': 17, 'threshold': 37.5, 'inequality_sign': 'less_than', 'alpha': 0.07859662885189661}, {'dimension': 9, 'threshold': 2.0, 'inequality_sign': 'less_than', 'alpha': 0.07142863634550768}, {'dimension': 5, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.07830753154662261}, {'dimension': 4, 'threshold': 28.799999999999997, 'inequality_sign': 'less_than', 'alpha': 0.07606159074712755}, {'dimension': 4, 'threshold': 19.2, 'inequality_sign': 'greater_than', 'alpha': 0.08306752811081908}, {'dimension': 7, 'threshold': 4.2, 'inequality_sign': 'greater_than', 'alpha': 0.08304167411411778}, {'dimension': 3, 'threshold': 92.0, 'inequality_sign': 'less_than', 'alpha': 0.08893356802801176}, {'dimension': 14, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.07000509315417822}, {'dimension': 7, 'threshold': 5.3999999999999995, 'inequality_sign': 'less_than', 'alpha': 0.07697582358566012}, {'dimension': 18, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.08507457442866745}, {'dimension': 5, 'threshold': 3.2, 'inequality_sign': 'less_than', 'alpha': 0.06765903873020729}, {'dimension': 7, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.08045680822237077}, {'dimension': 12, 'threshold': 1.2, 'inequality_sign': 'less_than', 'alpha': 0.05616862921969537}, {'dimension': 11, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.06454264376249834}, {'dimension': 7, 'threshold': 5.3999999999999995, 'inequality_sign': 'less_than', 'alpha': 0.053088884353829344}, {'dimension': 11, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.07346058614788575}, {'dimension': 13, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.07872267320907471}]
error rate of training set: 19.732%
error rate of test set: 19.403%
本文来自博客园,作者:EisenJi,转载请注明原文链接:https://www.cnblogs.com/eisenji/p/16423610.html




