机器学习(二十七)— EM算法
1、EM算法要解决的问题
如果使用基于最大似然估计的模型,模型中存在隐变量,就要用EM算法做参数估计。
EM算法解决这个的思路是使用启发式的迭代方法,既然我们无法直接求出模型分布参数,那么我们可以先猜想隐含数据(EM算法的E步),接着基于观察数据和猜测的隐含数据一起来极大化对数似然,求解我们的模型参数(EM算法的M步)。由于我们之前的隐藏数据是猜测的,所以此时得到的模型参数一般还不是我们想要的结果。不过没关系,我们基于当前得到的模型参数,继续猜测隐含数据(EM算法的E步),然后继续极大化对数似然,求解我们的模型参数(EM算法的M步)。以此类推,不断的迭代下去,直到模型分布参数基本无变化,算法收敛,找到合适的模型参数。
从上面的描述可以看出,EM算法是迭代求解最大值的算法,同时算法在每一次迭代时分为两步,E步和M步。一轮轮迭代更新隐含数据和模型分布参数,直到收敛,即得到我们需要的模型参数。
一个最直观了解EM算法思路的是K-Means算法,见之前写的K-Means聚类算法原理。在K-Means聚类时,每个聚类簇的质心是隐含数据。我们会假设KK个初始化质心,即EM算法的E步;然后计算得到每个样本最近的质心,并把样本聚类到最近的这个质心,即EM算法的M步。重复这个E步和M步,直到质心不再变化为止,这样就完成了K-Means聚类。
当然,K-Means算法是比较简单的,实际中的问题往往没有这么简单。上面对EM算法的描述还很粗糙,我们需要用数学的语言精准描述。
2、算法基本思想
理解算法:https://www.jianshu.com/p/1121509ac1dc
通过优化目标函数的下界,间接优化目标函数。受初值影响大,不能保证全局最优,但保证收敛到稳定点。
如果我们从算法思想的角度来思考EM算法,我们可以发现我们的算法里已知的是观察数据,未知的是隐含数据和模型参数,在E步,我们所做的事情是固定模型参数的值,优化隐含数据的分布,而在M步,我们所做的事情是固定隐含数据分布,优化模型参数的值。比较下其他的机器学习算法,其实很多算法都有类似的思想。
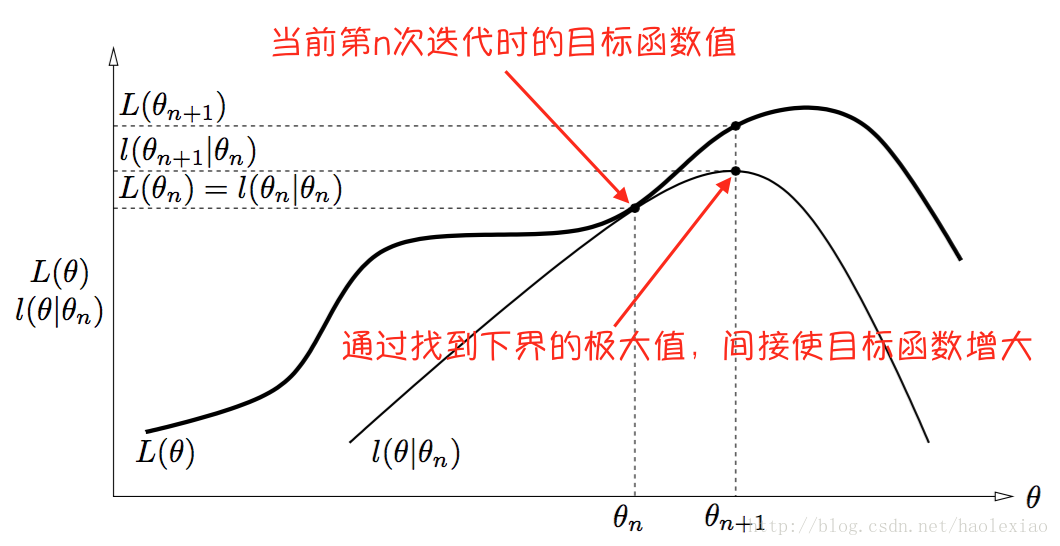
EM算法的优化过程直观理解是如下图的,即当前节点θn是如下的位置 然后找到当前函数的一个下界,且这个下界是可以在θn节点取到的.然后再找出这个下界的最大值,其横坐标就为θn+1所以上面找下界的步骤是E步骤,找下界最大值求出θn+1的步骤是M步骤。
3、算法步骤



 浙公网安备 33010602011771号
浙公网安备 33010602011771号