机器学习(二十一)— 特征工程、特征选择、特征归一化、特征离散化
特征工程:特征选择,特征表达和特征预处理。
1、特征选择
特征选择也被称为变量选择和属性选择,它能够自动地选择数据中目标问题最为相关的属性。是在模型构建时中选择相关特征子集的过程。
特征选择与降维不同。虽说这两种方法都是要减少数据集中的特征数量,但降维相当于对所有特征进行了重新组合,而特征选择仅仅是保留或丢弃某些特征,而不改变特征本身。降维常见的方法有PCA,SVD,萨蒙映射等,特征选择是丢弃作用小的特征。
为什么要做特征选择?
在有限的样本数目下,用大量的特征来设计分类器计算开销太大而且分类性能差。通过特征选取,删选掉冗余重复的和不相关的特征来进一步降维,获取尽可能小的特征子集,模型仅需少量的样本就可以得到较高的预测准确率。特征选择可以移除那些重复冗余、无关的特征,利于构建复杂度更低、解释性更强的模型。
1、去除冗余和不相关的特征,减少了特征维度,有利于提高模型的预测能力,构建效率更高的模型。2、更好地理解数据生成的过程,模型的解释性更强。
特征选择方法有很多,一般分为三类:
(1)第一类Filter(过滤法)比较简单,它按照特征的发散性或者相关性指标对各个特征进行评分,即给每一维的特征赋予权重,这样的权重就代表着该维特征的重要性,然后依据权重排序。设定评分阈值或者待选择阈值的个数,选择合适特征。
使用方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征,即去除取值变化小的特征。
卡方检验,经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值,因变量有M种取值,考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距,构建统计量。拿观察的现象推测结果。用方差来衡量某个观测频率和理论频率之间差异性的方法。
个人经验是,在没有什么思路的 时候,可以优先使用卡方检验和互信息、信息增益来做特征选择。
(2)第二类是Wrapper(包装法),根据目标函数,通常是预测效果评分,每次选择部分特征,或者排除部分特征。
将子集的选择看作是一个搜索寻优问题,生成不同的组合,对组合进行评价,再与其他的组合进行比较。这样就将子集的选择看作是一个是一个优化问题,这里有很多的优化算法可以解决,尤其是一些启发式的优化算法。一般我们会在不同的子集上构建模型,再利用模型的预测准确率来对不同的特征子集打分。搜索方法可以是随机式的,例如随机爬山法,也可以是启发式的,例如前向迭代和反向迭代。
(3)第三类Embedded(嵌入法)则稍微复杂一点,它先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小来选择特征。类似于过滤法,但是它是通过机器学习训练来确定特征的优劣,而不是直接从特征的一些统计学指标来确定特征的优劣。
正则化,回归模型,SVM,决策树,随机森林。
其中回归模型学习,越是重要的特征在模型中对应的系数就会越大,而跟输出变量越是无关的特征对应的系数就会越接近于0。
正则化,L1正则化将系数w的l1范数作为惩罚项加到损失函数上,由于正则项非零,这就迫使那些弱的特征所对应的系数变成0。因此L1正则化往往会使学到的模型很稀疏(系数w经常为0),这个特性使得L1正则化成为一种很好的特征选择方法。L1正则化像非正则化线性模型一样也是不稳定的,如果特征集合中具有相关联的特征,当数据发生细微变化时也有可能导致很大的模型差异。
L2正则化将系数向量的L2范数添加到了损失函数中。由于L2惩罚项中系数是二次方的,这使得L2和L1有着诸多差异,最明显的一点就是,L2正则化会让系数的取值变得平均。对于关联特征,这意味着他们能够获得更相近的对应系数。L2正则化对于特征选择来说一种稳定的模型,不像L1正则化那样,系数会因为细微的数据变化而波动。所以L2正则化和L1正则化提供的价值是不同的,L2正则化对于特征理解来说更加有用:表示能力强的特征对应的系数是非零。
随机森林,是一种非常流行的特征选择方法,它易于使用,一般不需要feature engineering、调参等繁琐的步骤,并且很多工具包都提供了平均不纯度下降方法。它的两个主要问题,1是重要的特征有可能得分很低(关联特征问题),2是这种方法对特征变量类别多的特征越有利(偏向问题)。
GBDT,梯度提升树。在Kaggle之类的算法竞赛中,高分团队主要使用的方法除了集成学习算法,剩下的主要就是在高级特征上面做文章。所以寻找高级特征是模型优化的必要步骤之一。当然,在第一次建立模型的时候,我们可以先不寻找高级特征,得到以后基准模型后,再寻找高级特征进行优化。
寻找高级特征最常用的方法有:
- 若干项特征加和: 我们假设你希望根据每日销售额得到一周销售额的特征。你可以将最近的7天的销售额相加得到。
- 若干项特征之差: 假设你已经拥有每周销售额以及每月销售额两项特征,可以求一周前一月内的销售额。
- 若干项特征乘积: 假设你有商品价格和商品销量的特征,那么就可以得到销售额的特征。
- 若干项特征除商: 假设你有每个用户的销售额和购买的商品件数,那么就是得到该用户平均每件商品的销售额。
当然,寻找高级特征的方法远不止于此,它需要你根据你的业务和模型需要而得,而不是随便的两两组合形成高级特征,这样容易导致特征爆炸,反而没有办法得到较好的模型。个人经验是,聚类的时候高级特征尽量少一点,分类回归的时候高级特征适度的多一点。
2、特征表达、离散化&连续化
即如果对某一个特征的具体表现形式做处理。主要包括缺失值处理,特殊的特征处理比如时间和地理位置处理,离散特征的连续化和离散化处理,连续特征的离散化处理几个方面。
越是离散的特征、越是非线性模型,其建模能力越强。
离散化优点:
- 离散化之后的特征对于异常数据具有很强的鲁棒性。能够对抗过拟合的原因:经过特征离散化之后,模型不再拟合特征的具体值,而是拟合特征的某个概念。因此能够对抗数据的扰动,更具有鲁棒性。对异常离群点有很强的鲁棒性;
- 缺失值处理:可以单独分为一类进入模型;
- 特征离散化之后,相当于引入了非线性,提升模型的表达能力,增强拟合能力。采用例如 one-hot 形式表示,能为每个类别(或桶)附以单独的权重;
- 模型会更稳定。使得模型要拟合的值大幅度降低,也降低了模型的复杂度。同时降低模型过拟合的风险,不会因为特征的小变动导致完全不同的输出;
- 离散特征的增加和减少都较容易,有利于模型迭代;
分桶是离散化的常用方法,将连续型特征离线化为一系列 0/1 的离散特征;当数值特征跨越不同的数量级的时候,模型可能会只对大的特征值敏感,这种情况可以考虑分桶操作。分桶操作可以看作是对数值变量的离散化,之后通过二值化进行 one-hot 编码。分桶的数量和宽度可以根据业务领域的经验来指定,但也有一些常规的做法:
- 分桶后得到的稀疏向量,内积乘法运算速度更快,计算结果更方便存储;
- 对异常数据有很强的鲁棒性
选择分桶方式:
- 等距分桶。每个桶的宽度是固定的,即值域范围是固定的,比如是 0-99,100-199,200-299等;这种适合样本分布比较均匀的情况,避免出现有的桶的数量很少,而有的桶数量过多的情况;对数变换是处理具有重尾分布的正数的有力工具。(重尾分布在尾部范围内的概率比高斯分布的概率大)。它将分布在高端的长尾压缩成较短的尾部,并将低端扩展成较长的头部。
- 等频分桶,也称为分位数分桶。也就是每个桶有一样多的样本,但可能出现数值相差太大的样本放在同个桶的情况;
- 模型分桶。使用模型找到最佳分桶,比如聚类,将特征分成多个类别,或者树模型,这种非线性模型天生具有对连续型特征切分的能力,利用特征分割点进行离散化。
需要注意:
- 要让桶内的属性取值变化对样本标签的影响基本在一个不大的范围,即不能出现单个桶内,样本取值变化很大的情况;
- 每个桶内都有足够的样本,如果样本太少,随机性太大,不具有统计意义上的说服力;
- 每个桶内的样本进行分布均匀;
3、特征预处理
(1)特征归一化:
0、为什么一些机器学习模型需要对数据进行归一化?
- 归一化后加快了梯度下降求最优解的速度,消除样本数据或者特征之间的量纲影响,即消除特征间单位和尺度差异的影响;加快学习算法的收敛速度。
- 归一化有可能提高精度,避免量级较大的属性占据主导地位,以对每维特征同等看待;使不同量纲的特征处于同一数值量级,减少方差大的特征的影响,使模型更准确。
有哪些方法:
(1) z-score标准化:这是最常见的特征预处理方式,基本所有的线性模型在拟合的时候都会做 z-score标准化。具体的方法是求出样本特征x的均值mean和标准差std,然后用(x-mean)/std来代替原特征。这样特征就变成了均值为0,方差为1了。每维特征0均值1方。
(2) max-min标准化:也称为离差标准化,预处理后使特征值映射到[0,1]之间。具体的方法是求出样本特征x的最大值max和最小值min,然后用(x-min)/(max-min)来代替原特征。如果我们希望将数据映射到任意一个区间[a,b],而不是[0,1],那么也很简单。用(x-min)(b-a)/(max-min)+a来代替原特征即可。
(3) Mean normalization:同时用最大值最小值的差对特征进行归一化,(x-mean)/(max-min);
(4) 将每个样本的特征向量除以其长度,即对样本特征向量的长度进行归一化,长度的度量常使用的是L2 norm(欧氏距离),有时也会采用L1 norm;
经常我们还会用到中心化,主要是在PCA降维的时候,此时我们求出特征x的平均值mean后,用x-mean代替原特征,也就是特征的均值变成了0, 但是方差并不改变。这个很好理解,因为PCA就是依赖方差来降维的,如果我们做了z-score标准化,所以特征的方差为1,那么就没法来降维了。
-
以上归一化方法的优缺点:
总的来说,归一化/标准化的目的是为了获得某种“无关性”——偏置无关、尺度无关、长度无关……当归一化/标准化方法背后的物理意义和几何含义与当前问题的需要相契合时,其对解决该问题就有正向作用,反之,就会起反作用。所以,“何时选择何种方法”取决于待解决的问题,即problem-dependent。
前3种feature scaling的计算方式为减一个统计量再除以一个统计量,最后1种为除以向量自身的长度。
- 减一个统计量可以看成选哪个值作为原点,是最小值还是均值,并将整个数据集平移到这个新的原点位置。如果特征间偏置不同对后续过程有负面影响,则该操作是有益的,可以看成是某种偏置无关操作;如果原始特征值有特殊意义,比如稀疏性,该操作可能会破坏其稀疏性。
- 除以一个统计量可以看成在坐标轴方向上对特征进行缩放,用于降低特征尺度的影响,可以看成是某种尺度无关操作。缩放可以使用最大值最小值间的跨度,也可以使用标准差(到中心点的平均距离),前者对outliers敏感,outliers对后者影响与outliers数量和数据集大小有关,outliers越少数据集越大影响越小。
- 除以长度相当于把长度归一化,把所有样本映射到单位球上,可以看成是某种长度无关操作,比如,词频特征要移除文章长度的影响,图像处理中某些特征要移除光照强度的影响,以及方便计算余弦距离或内积相似度等。
虽然大部分机器学习模型都需要做标准化和归一化,也有不少模型可以不做做标准化和归一化,主要是基于概率分布的模型,比如决策树大家族的CART,随机森林等。当然此时使用标准化也是可以的,大多数情况下对模型的泛化能力也有改进。
(2)异常特征样本清洗
(3)样本不平衡:一般是两种方法:权重法或者采样法
(2)标准化与归一化区别

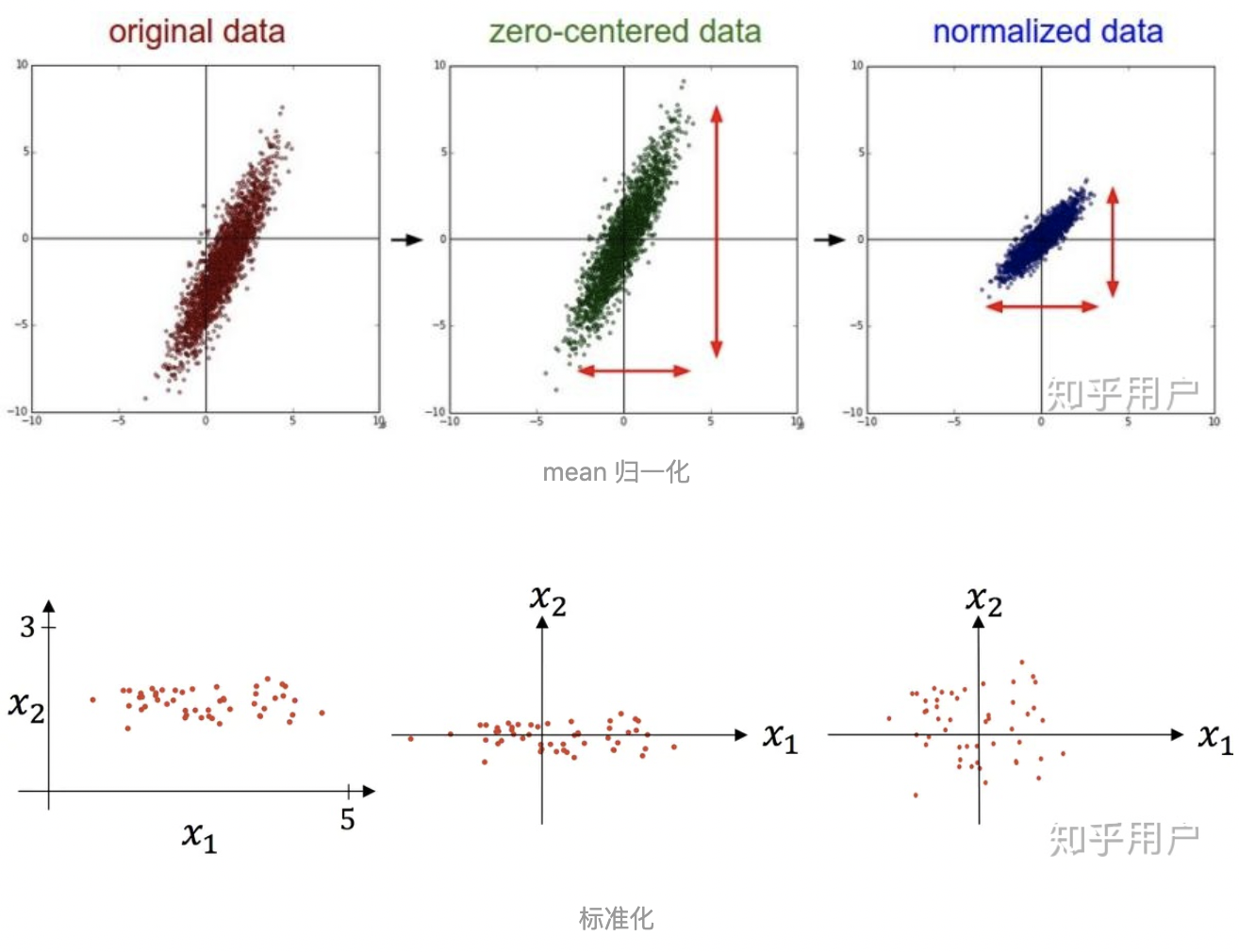
可以看到 mean 归一化和标准化都将数据分布中心移到原点,
归一化没有改变数据分布的形状,而标准化使样本数据的分布近似为某种分布(通常为正态分布)。
(3)特征编码
(1)序号编码(Ordinal Encoding)
定义:序号编码一般用于处理类别间具有大小关系的数据。
比如成绩,可以分为高、中、低三个档次,并且存在“高>中>低”的大小关系,那么序号编码可以对这三个档次进行如下编码:高表示为 3,中表示为 2,低表示为 1,这样转换后依然保留了大小关系。
(2)独热编码(One-hot Encoding)
定义:独热编码通常用于处理类别间不具有大小关系的特征。
独热编码的优点有以下几个:
- 能够处理非数值属性。比如血型、性别等
- 一定程度上扩充了特征。
- 编码后的向量是稀疏向量,只有一位是 1,其他都是 0,可以利用向量的稀疏来节省存储空间。
- 能够处理缺失值。当所有位都是 0,表示发生了缺失。此时可以采用处理缺失值提到的高维映射方法,用第 N+1 位来表示缺失值。
当然,独热编码也存在一些缺点:高维度特征会带来以下几个方面问题:
- KNN 算法中,高维空间下两点之间的距离很难得到有效的衡量;
- 逻辑回归模型中,参数的数量会随着维度的增高而增加,导致模型复杂,出现过拟合问题;
- 通常只有部分维度是对分类、预测有帮助,需要借助特征选择来降低维度。
参考文献:https://blog.csdn.net/lc013/article/details/104454135



 浙公网安备 33010602011771号
浙公网安备 33010602011771号