代码题（18）— 子集

1、78. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

方法1：使用循环

　　我们可以一位一位的往上叠加，比如对于题目中给的例子[1,2,3]来说，最开始是空集，那么我们现在要处理1，就在空集上加1，为[1]，现在我们有两个自己[]和[1]，下面我们来处理2，我们在之前的子集基础上，每个都加个2，可以分别得到[2]，[1, 2]，那么现在所有的子集合为[], [1], [2], [1, 2]，同理处理3的情况可得[3], [1, 3], [2, 3], [1, 2, 3], 再加上之前的子集就是所有的子集合了，代码如下：

以集合{1,2,3}为例。

初始化：[[]]

第一步：[[],[1]]（在上面的结果的子集上添加元素1并上面的集合）

第二步：[[],[1],[2],[1,2]]（上第二步结果上每个子集添加元素2并上面的集合）

第三步：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]（…）

整个添加的顺序为：

[]
[1]
[2]
[1 2]
[3]
[1 3]
[2 3]
[1 2 3]

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        vector<int> temp;
        sort(nums.begin(), nums.end());
        res.push_back(temp);
        for (int i = 0; i < nums.size(); ++i) {
            int size = res.size();
            for (int j = 0; j < size; ++j) {
                res.push_back(res[j]);//加入一个之前有的
                res.back().push_back(nums[i]);//对最后加入的那个数组插入一个数
            }
        }
        return res;
    }
};

方法2：

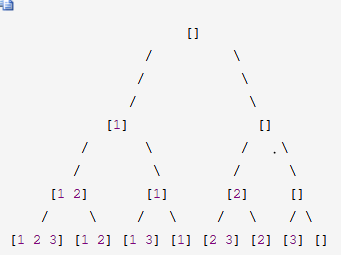
　　下面来看递归的解法，相当于一种深度优先搜索。由于原集合每一个数字只有两种状态，要么存在，要么不存在，那么在构造子集时就有选择和不选择两种情况，所以可以构造一棵二叉树，左子树表示选择该层处理的节点，右子树表示不选择，最终的叶节点就是所有子集合，树的结构如下：

整个添加的顺序为：

[]
[1]
[1 2]
[1 2 3]
[1 3]
[2]
[2 3]
[3]

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        vector<int> temp;
        sort(nums.begin(), nums.end());
        getSub(nums, 0, temp, res);
        return res;
        
    }
    void getSub(vector<int> &nums, int pos, vector<int> &temp, vector<vector<int>> &res)
    {
        res.push_back(temp);
        for(int i=pos;i<nums.size();++i)
        {
            temp.push_back(nums[i]);
            getSub(nums, i + 1, temp, res);
            temp.pop_back();
        }
    }
};

方法三： 

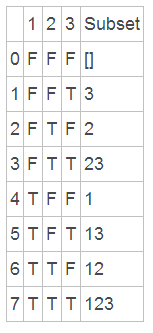
　　把数组中所有的数分配一个状态，true表示这个数在子集中出现，false表示在子集中不出现，那么对于一个长度为n的数组，每个数字都有出现与不出现两种情况，所以共有2ⁿ中情况，那么我们把每种情况都转换出来就是子集了，我们还是用题目中的例子, [1 2 3]这个数组共有8个子集，每个子集的序号的二进制表示，把是1的位对应原数组中的数字取出来就是一个子集，八种情况都取出来就是所有的子集了。

2、90. 子集 II

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

在处理到第二个2时，由于前面已经处理了一次2，这次我们只在添加过2的[2] 和 [1 2]后面添加2，其他的都不添加，那么这样构成的二叉树如下图所示：

                        []        
                   /          \        
                  /            \     
                 /              \
              [1]                []
           /       \           /    \
          /         \         /      \        
       [1 2]       [1]       [2]     []
      /     \     /   \     /   \    / \
  [1 2 2] [1 2]  X   [1]  [2 2] [2] X  []

代码只需在原有的基础上增加一句话，while (S[i] == S[i + 1]) ++i; 这句话的作用是跳过树中为X的叶节点，因为它们是重复的子集，应被抛弃。代码如下：

class Solution {
public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<vector<int>> res;
        if(nums.empty())
            return res;
        vector<int> temp;
        sort(nums.begin(),nums.end());
        subsetsDfs(nums,0,temp,res);
        return res;
    }
    void subsetsDfs(vector<int>& nums, int pos, vector<int>& temp, vector<vector<int>> &res )
    {
        res.push_back(temp);
        for(int i=pos;i<nums.size();++i)
        {
            if(i>pos && nums[i] == nums[i-1])
                continue;
                
            temp.push_back(nums[i]);
            subsetsDfs(nums,i+1,temp,res);
            temp.pop_back();
        }
        
    }
};