代码题（12）— 二分查找、搜索插入位置、x 的平方根

1、704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.empty())
            return -1;
        int low = 0;
        int high = nums.size()-1; //此处是减1，下面就是 <= 
        while(low <= high)
        {
            int mid = (low+high)/2;
            if(nums[mid] == target)
                return mid;
            else if(nums[mid] > target)
                high = mid-1;
            else
                low = mid+1;
        }
        return -1;
    }
};

 2、35. 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

输入: [1,3,5,6], 5
输出: 2

示例 2:

输入: [1,3,5,6], 2
输出: 1

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        if(nums.empty())
            return -1;
        int low = 0;
        int high = nums.size()-1;
        int mid = 0;
        while(low <= high)
        {
            mid = (low + high)*0.5;
            if(target < nums[mid])
                high = mid-1;
            else if(target > nums[mid])
                low = mid+1;
            else
                return mid;
        }
        return high+1;
    }
};

3、 69. x 的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

（1）二分法

class Solution {
public:
    int mySqrt(int x) {
        if(x <= 0)
            return 0;
        long long left = 1, right = x, res = -1;
        while(left <= right){
            long long mid = left + (right - left)/2;
            if(mid * mid <= x) {
                res = mid;
                left = mid + 1;
            } else 
                right = mid - 1;
        }
        return res;
    }
};

（2）牛顿法，不使用二分法

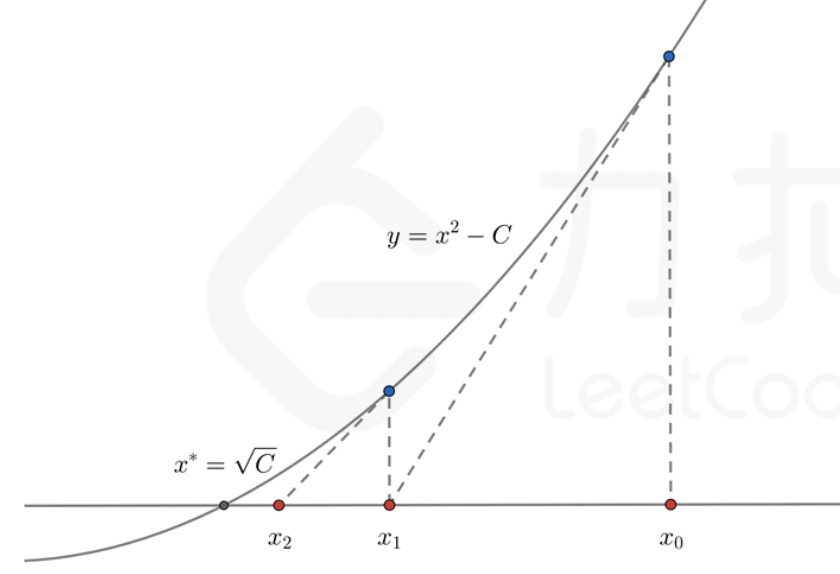
使用泰勒展开式，也就是某一点的切线方程， 经过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f'(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f'(x_i)。

继续化简，x_i+1=x_i - (x_i² - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2。

class Solution {
public:
    int mySqrt(int x) {
        if(x <= 0)
            return 0;
        long long res = x;
        while(res * res > x){
            res = (res + x/res)/2;
        }
        return res;
    }
};