代码题（4）— 二叉树展开为链表、二叉搜索树与双向链表

1、114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

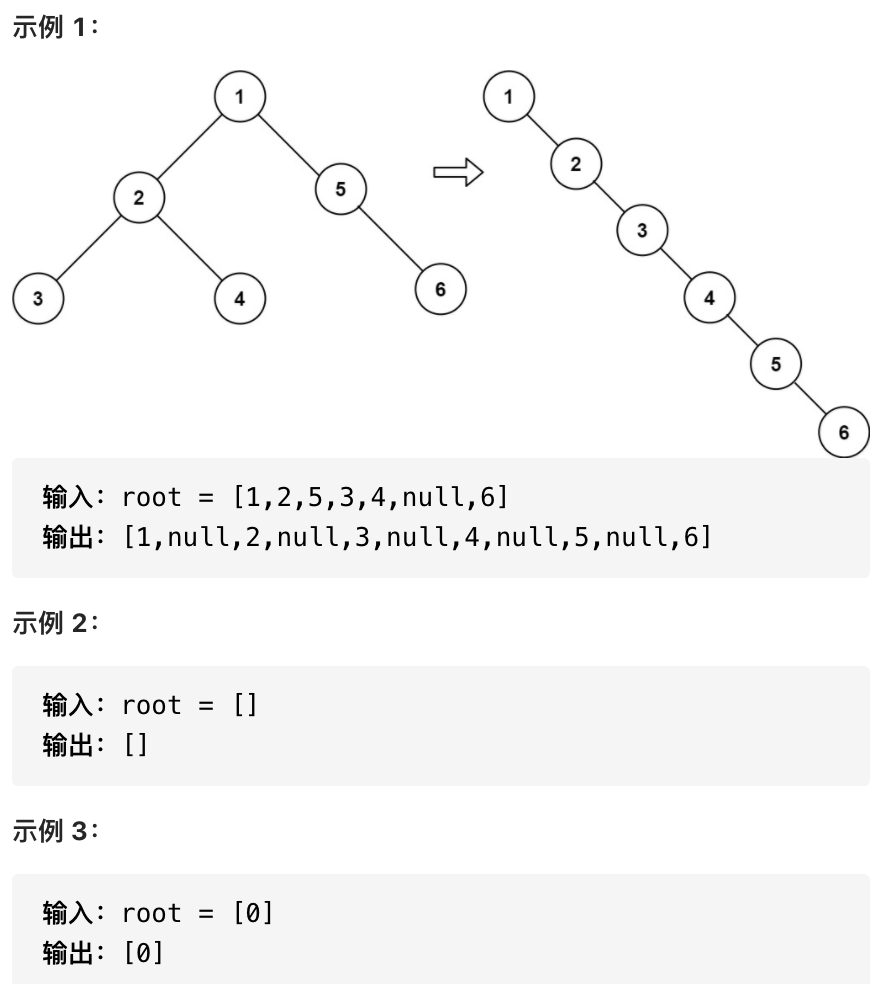
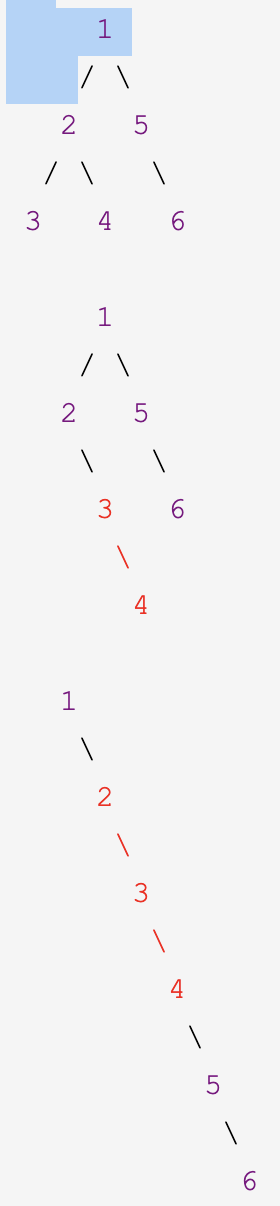
这个方法是从根节点开始出发，先检测其左子结点是否存在，如存在则将根节点和其右子节点断开，将左子结点及其后面所有结构一起连到原右子节点的位置，把原右子节点连到元左子结点最后面的右子节点之后。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        if(root == nullptr)
            return;
        TreeNode* cur = root;
        while(cur){
            if(cur->left){
                TreeNode* p = cur->left;
                while(p->right)
                    p = p->right;
                p->right = cur->right;
                cur->right = cur->left;
                cur->left = nullptr;

            }
            cur = cur->right;
        }
    }
};

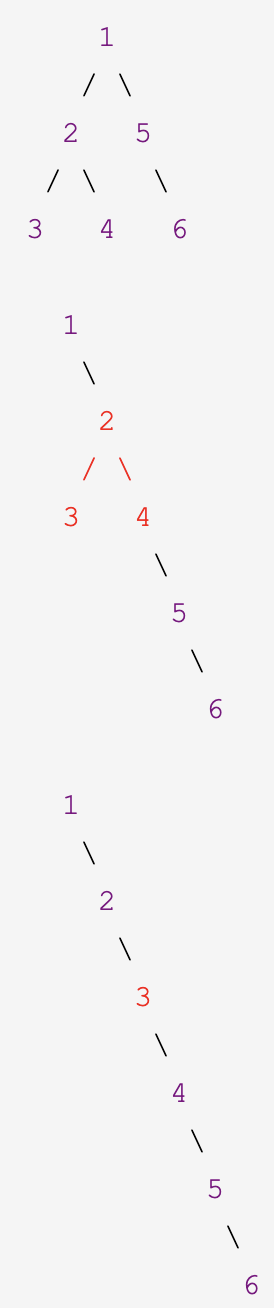
 递归版本：

根据展开后形成的链表的顺序分析出是使用先序遍历，那么只要是数的遍历就有递归和非递归的两种方法来求解，这里我们也用两种方法来求解。首先来看递归版本的，思路是先利用 DFS 的思路找到最左子节点，然后回到其父节点，把其父节点和右子节点断开，将原左子结点连上父节点的右子节点上，然后再把原右子节点连到新右子节点的右子节点上，然后再回到上一父节点做相同操作。代码如下：

class Solution {
public:
    void flatten(TreeNode* root) {
        if(root == nullptr)
            return;
        if(root->left)
            flatten(root->left);
        if(root->right)
            flatten(root->right);
        TreeNode* tmp = root->right;
        root->right = root->left;
        root->left = nullptr;
        while(root->right)
            root = root->right;
        root->right = tmp;

    }
};

2、 二叉搜索树与双向链表

 输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

class Solution {
public:
    TreeNode* Convert(TreeNode* pRoot)
    {
        //递归
        //判断边界
        if(pRoot==nullptr)
            return pRoot;
        if(pRoot->left==nullptr && pRoot->right==nullptr)
            return pRoot;
        // 1.将左子树构造成双链表，并返回链表头节点
        TreeNode *left=Convert(pRoot->left);
        // 2.定位至左子树双链表最后一个节点
        TreeNode *p=left;
        while(p!=nullptr && p->right!=nullptr)
            p=p->right;
        // 3.如果左子树链表不为空的话，将当前root追加到左子树链表。
        if(left!=nullptr)
        {
            p->right=pRoot;
            pRoot->left=p;
        }
        // 4.将右子树构造成双链表，并返回链表头节点
        TreeNode *right=Convert(pRoot->right);
        // 5.如果右子树链表不为空的话，将该链表追加到root节点之后
        if(right!=nullptr)
        {
            pRoot->right=right;
            right->left=pRoot;
        }
        // 6.根据左子树链表是否为空确定返回的节点。
        return left!=nullptr?left:pRoot;
    }
};