机器学习（十三）— 相似性度量和距离计算
在机器学习中，经常需要使用距离和相似性计算的公式，在做分类时，常常需要计算不同样本之间的相似性度量(Similarity Measurement)，计算这个度量，我们通常采用的方法是计算样本之间的“距离(Distance)”。比如利用k-means进行聚类时，判断个体所属的类别，就需要使用距离计算公式得到样本距离簇心的距离，利用kNN进行分类时，也是计算个体与已知类别之间的相似性，从而判断个体的所属类别。
1、 欧式距离(Euclidean Distance)
普通欧式距离的计算：
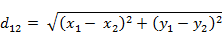
标准化欧式距离(Standardized Euclidean Distance )：将各个分量都“标准化”到均值、方差相等，标准化后的值 = ( 标准化前的值 － 分量的均值 ) /分量的标准差。
2、曼哈顿距离(Manhattan Distance)
从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源， 曼哈顿距离也称为城市街区距离(City Block distance)。
二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离：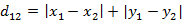
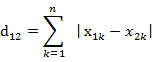
3、切比雪夫距离 ( Chebyshev Distance )
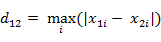
等价形式：
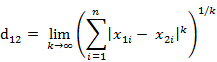
小结：曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
举个例子：二维样本(身高,体重)，其中身高范围是150 ~ 190，体重范围是50 ~ 60，有三个样本：a(180,50)，b(190,50)，c(180,60)。那么a与b之间的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c之间的闵氏距离，但是身高的10cm真的等价于体重的10kg么？因此用闵氏距离来衡量这些样本间的相似度很有问题。
简单说来，闵氏距离的缺点主要有两个：(1)将各个分量的量纲(scale)，也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布（期望，方差等)可能是不同的。
4、马氏距离(Mahalanobis Distance)
有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到u的马氏距离表示为：
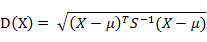
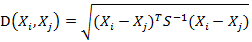
5、夹角余弦(Cosine)
几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。
夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小，夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向完全相反夹角余弦取最小值-1。
对于两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)，可以使用类似于夹角余弦的概念来衡量它们间的相似程度。
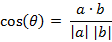
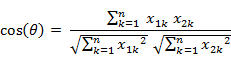
余弦距离与欧式距离的区别：
欧氏距离和余弦距离各自有不同的计算方式和衡量特征，因此它们适用于不同的数据分析模型：
欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异。
余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦距离对绝对数值不敏感）。
6、汉明距离(Hamming distance)
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
应用：信息编码（为了增强容错性，应使得编码间的最小汉明距离尽可能大）。
参考：http://www.cnblogs.com/xbinworld/archive/2012/09/24/2700572.html#top
