深度学习—常见激活函数对比
1、为什么使用激活函数?
如果不用激励函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
2、为什么分类问题不能使用mse损失函数?
-
在线性回归中用到的最多的是MSE(最小二乘损失函数),这个比较好理解,就是预测值和目标值的欧式距离。而交叉熵是一个信息论的概念,交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
所以交叉熵本质上是概率问题,表征真实概率分布与预测概率分布差异,和几何上的欧氏距离无关,在线性回归中才有欧氏距离的说法,在分类问题中label的值大小在欧氏空间中是没有意义的。所以分类问题不能用mse作为损失函数。 -
分类问题是逻辑回归,必须有激活函数这个非线性单元在,比如sigmoid(也可以是其他非线性激活函数),mse已经是非凸函数了,有多个极值点,所以不适用做损失函数了。
-
mse作为损失函数,求导的时候都会有对激活函数的求导连乘运算,对于sigmoid、tanh,有很大区域导数为0的。该激活函数的输入很可能直接就在平坦区域,那么导数就几乎是0,梯度就几乎不会被反向传递,梯度直接消失了。所以mse做损失函数的时候最后一层不能用sigmoid做激活函数,其他层可以用sigmoid做激活函数。当然,用其他损失函数只能保证在第一步不会直接死掉,反向传播如果激活函数和归一化做得不好,同样会梯度消失。所以从梯度这个原因说mse不好不是很正确。
梯度消失问题存在2个地方:
1.损失函数对权值w求导,这是误差反向传播的第一步,mse的损失函数会在损失函数求导这一个层面上就导致梯度消失;所以使用交叉熵损失函数。
2.误差反向传播时,链式求导也会使得梯度消失。使用交叉熵损失函数也不能避免反向传播带来的梯度消失,此时规避梯度消失的方法:
- ReLU等激活函数;
- 输入归一化、每层归一化;
- 网络结构上调整,比如LSTM、GRU等。
深度神经网络,不管用什么损失函数,隐含层的激活函数如果用sigmoid,肯定会梯度消失,训练无效。如果是浅层神经网络,影响可能不是很大,和神经网络的输入有关,如果输入经过了归一化,结果靠谱,如果没有归一化,梯度也直接消失,训练肯定失败。
损失函数和激活函数决定的是模型会不会收敛,也影响训练速度;优化器决定的是模型能不能跳出局部极小值、跳出鞍点、能不能快速下降这些问题的。
3、都有什么?
(1)sigmoid函数
公式:

曲线:
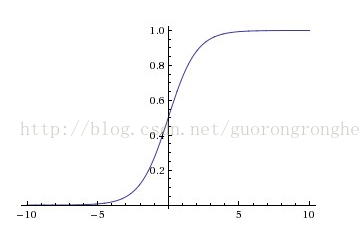
也叫 Logistic 函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。
在特征相差比较复杂或是相差不是特别大时效果比较好。
缺点:(1)容易产生梯度消失,导致训练出现问题,
(2)输出不是以0为中心的,模型收敛速度慢。
出现梯度消失原因:
1、当神经元的激活在接近0或1处时会饱和,在这些区域,梯度几乎为0。
在反向传播的时候,这个(局部)梯度将会与整个损失函数关于该门单元输出的梯度相乘。因此,如果局部梯度非常小,那么相乘的结果也会接近零,这会有效地“杀死”梯度,几乎就有没有信号通过神经元传到权重再到数据了。还有,为了防止饱和,必须对于权重矩阵初始化特别留意。比如,如果初始化权重过大,那么大多数神经元将会饱和,导致网络就几乎不学习了。
函数导数: ![]()
2、可以作为概率,但导数值小于1,最大为0.25,如果损失函数 mse,则梯度计算与 sigmoid 导数相关,导致梯度消失。
输出不是以0为中心问题:

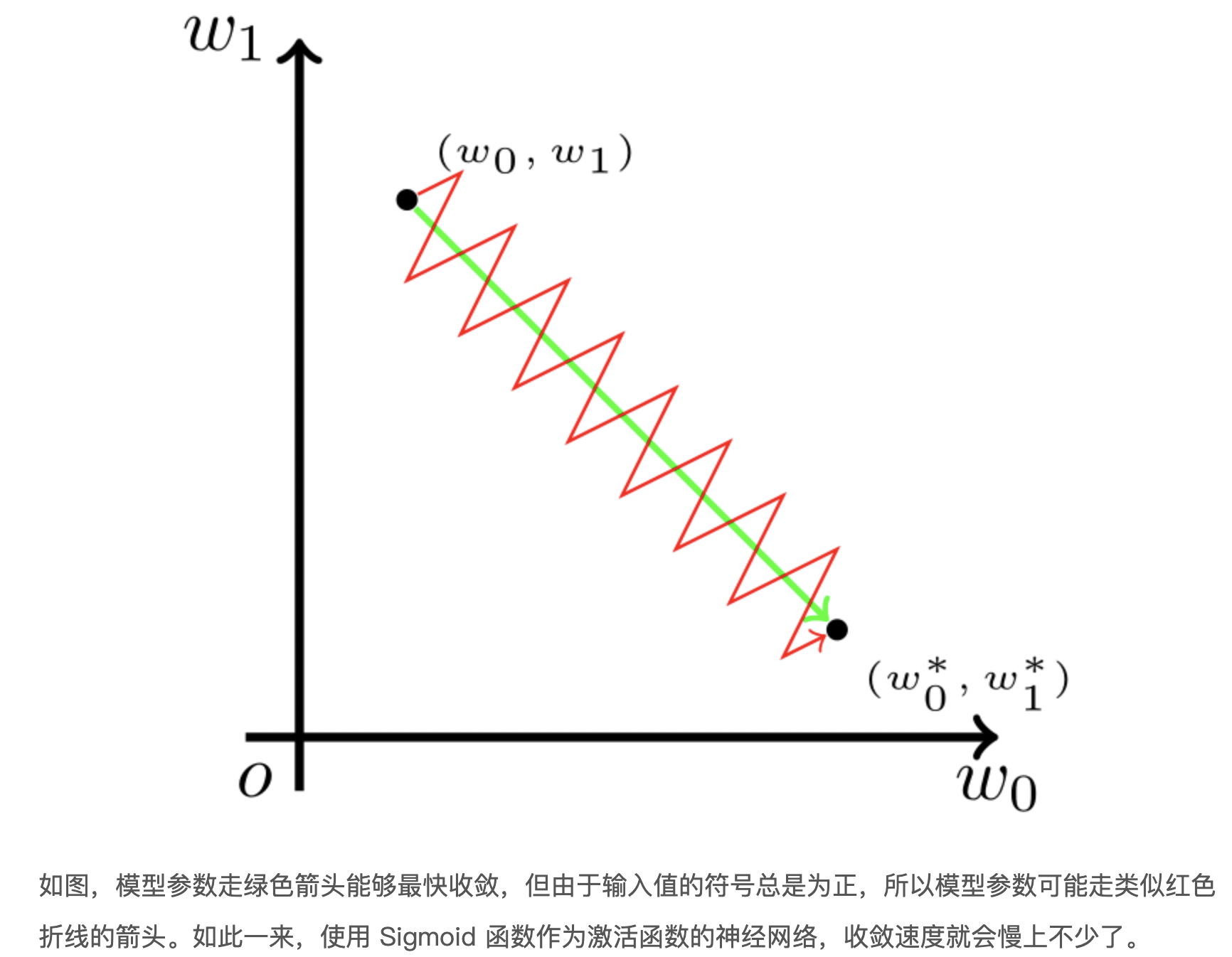
在 Sigmoid 函数中,输出值恒为正。这也就是说,如果上一级神经元采用 Sigmoid 函数作为激活函数,那么我们无法做到 x0 和 x1 符号相反。此时,模型为了收敛,不得不向逆风前行的风助力帆船一样,走 Z 字形逼近最优解。
(2)Tanh函数
公式:双曲正切函数,tanh神经元是一个简单放大的sigmoid神经元,
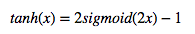
曲线:

tanh非线性函数图像如上图右边所示。它将实数值压缩到[-1,1]之间。和sigmoid神经元一样,它也存在饱和问题,但是和sigmoid神经元不同的是,它的输出是零中心的。因此,在实际操作中,tanh非线性函数比sigmoid非线性函数更受欢迎。tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
(3)ReLU
Rectified Linear Unit(ReLU) - 用于隐层神经元输出。
公式:

曲线:

优点:
(1)ReLU 在x0时导数为 1,所以,ReLU 能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。
(2)relu函数在负半区的导数为0 ,所以一旦神经元激活值进入负半区,那么梯度就会为0,造成了网络的稀疏性,缓解过拟合。
(3)relu计算简单,采用sigmoid等函数,反向传播求误差梯度时,计算量大,而采用Relu激活函数,整个过程的计算量节省很多。
缺点:
在训练的时候,ReLU单元比较脆弱并且可能“死掉”。举例来说,当一个很大的梯度流过ReLU的神经元的时候,可能会导致梯度更新到一种特别的状态,在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生,那么从此所以流过这个神经元的梯度将都变成0。也就是说,这个ReLU单元在训练中将不可逆转的死亡,因为这导致了数据多样化的丢失。例如,如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。
Q:relu是如何表现出高阶的非线性的组合的?
ReLU在正负半轴都是线性的,确实没错。但是,它实现网络非线性映射的魔法在于对不同样本的不同状态。考虑对于一个激活函数只包含ReLU和线性单元的简单网络:首先,我们考虑有一个输入样本 ,网络中所有的ReLU对它都有一个确定的状态,整个网络最终对
的映射等效于一个线性映射:
考虑另一个输入样本
,它的特征与
不同。因此,网络中某些ReLU的激活状态因为输入变化可能发生变化,比如一些以前在右侧接通区域的变到左侧切断区域(或反之);这样整个网络对于样本
有一个新的等效线性映射:
这两个函数都是线性的,但是他们的参数是不同的。进一步,可以这样设想,在
的周围,有一小块区域
(为了表达简单,假定了两侧
都是对称的,实际通常不是)。所有特征位于这一小块区域内的样本,在网络中激活的ReLU状态都和
激活的完全一样。(因为这些点离
非常接近,在这个变化范围,网络中所有的ReLU都没有翻转)。那么这一小块区域内,网络拟合的出的线性映射都是一样的,去掉x,y的角标,表示为
您一定发现了,这就是由
定义的一个超平面,但是这个超平面可能只在
的附近才成立。一旦稍微远离,导致至少一个ReLU翻转,那么网络将有可能拟合出另一个不同参数的超平面。
所以,这具有不同参数的超平面拼接在一起,不就拟合出了各种各样的非线性特性了吗?所以,虽然ReLU的每个部分都是线性的,但是通过对ReLU各种状态的组合进行改变,导致了网络等效映射的变化,也就构造了各种非线性映射。表现在多维空间,就是很多不同的小块超平面拼接成的奇形怪状的近似超曲面。
改进版,Leaky ReLU。
表达式:f(x) = max(0.01x, x)
曲线:
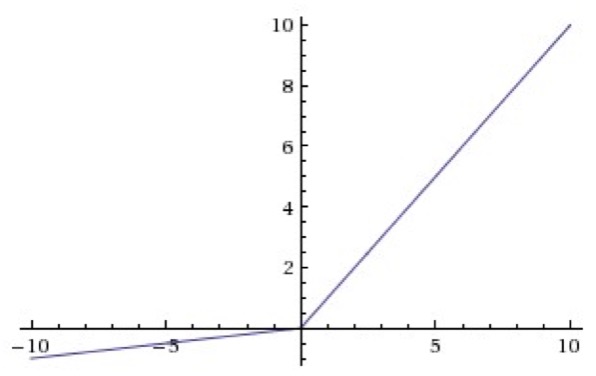
Leaky ReLU是为解决“ReLU死亡”问题的尝试。ReLU中当x<0时,函数值为0。而Leaky ReLU则是给出一个很小的负数梯度值,比如0.01。
有些研究者的论文指出这个激活函数表现很不错,但是其效果并不是很稳定。Kaiming He等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法PReLU,把负区间上的斜率当做每个神经元中的一个参数。然而该激活函数在在不同任务中均有益处的一致性并没有特别清晰。
(4)softmax函数
Softmax - 用于多分类神经网络输出。
公式:

就是如果某一个 zj 大过其他 z, 那这个映射的分量就逼近于 1,其他就逼近于 0,主要应用就是多分类。
为什么要取指数,第一个原因是要模拟 max 的行为,所以要让大的更大。第二个原因是需要一个可导的函数。
4. sigmoid ,ReLU, softmax 的比较
(1)Sigmoid 和 ReLU 比较:
(1)对于深层网络,sigmoid函数反向传播时,很容易就会出现梯度消失的情况(在sigmoid接近饱和区时,变换太缓慢,导数趋于0,这种情况会造成信息丢失)。而relu函数在大于0的部分梯度为常数,所以不会产生梯度弥散现象。
(2)relu函数在负半区的导数为0 ,所以一旦神经元激活值进入负半区,那么梯度就会为0,造成了网络的稀疏性,缓解过拟合。
(3)relu计算简单,采用sigmoid等函数,反向传播求误差梯度时,计算量大,而采用Relu激活函数,整个过程的计算量节省很多。
(2)Sigmoid 和 Softmax 区别:
sigmoid将一个real value映射到(0,1)的区间(当然也可以是(-1,1)),这样可以用来做二分类。
而softmax把一个k维的real value向量(a1,a2,a3,a4….)映射成一个(b1,b2,b3,b4….)其中 bi 是一个 0~1 的常数,输出神经元之和为 1.0,所以相当于概率值,然后可以根据 bi 的概率大小来进行多分类的任务。
二分类问题时 sigmoid 和 softmax 是一样的,求的都是 cross entropy loss,而 softmax 可以用于多分类问题。
多个logistic回归通过叠加也同样可以实现多分类的效果,但是 softmax回归进行的多分类,类与类之间是互斥的,即一个输入只能被归为一类;多个logistic回归进行多分类,输出的类别并不是互斥的,即"苹果"这个词语既属于"水果"类也属于"3C"类别。
总结:
(1)以上就是一些常用的神经元及其激活函数。最后需要注意一点:在同一个网络中混合使用不同类型的神经元是非常少见的,虽然没有什么根本性问题来禁止这样做。
(2)一句话:“那么该用那种呢?”用ReLU非线性函数。注意设置好学习率,或许可以监控你的网络中死亡的神经元占的比例。
(3)如果单元死亡问题困扰你,就试试Leaky ReLU或者Maxout,不要再用sigmoid了。也可以试试tanh,但是其效果应该不如ReLU或者Maxout。
参考文献:
https://www.jianshu.com/p/22d9720dbf1a



 浙公网安备 33010602011771号
浙公网安备 33010602011771号