推荐系统(17)—— 强化学习方法概述
0、什么是强化学习
强化学习是一类算法, 是让计算机实现从一开始什么都不懂, 脑袋里没有一点想法, 通过不断地尝试, 从错误中学习, 最后找到规律, 学会了达到目的的方法. 这就是一个完整的强化学习过程。
原来计算机也需要一位虚拟的老师, 这个老师比较吝啬, 他不会告诉你如何移动, 如何做决定, 他为你做的事只有给你的行为打分, 那我们应该以什么形式学习这些现有的资源, 或者说怎么样只从分数中学习到我应该怎样做决定呢? 很简单, 我只需要记住那些高分, 低分对应的行为, 下次用同样的行为拿高分, 并避免低分的行为.比如老师会根据我的开心程度来打分, 我开心时, 可以得到高分, 我不开心时得到低分. 有了这些被打分的经验, 我就能判断为了拿到高分, 我应该选择一张开心的脸, 避免选到伤心的脸. 这也是强化学习的核心思想. 可以看出在强化学习中, 一种行为的分数是十分重要的. 所以强化学习具有分数导向性. 我们换一个角度来思考.这种分数导向性好比我们在监督学习中的正确标签.
我们知道监督学习, 是已经有了数据和数据对应的正确标签, 比如这样. 监督学习就能学习出那些脸对应哪种标签. 不过强化学习还要更进一步, 一开始它并没有数据和标签.他要通过一次次在环境中的尝试, 获取这些数据和标签, 然后再学习通过哪些数据能够对应哪些标签, 通过学习到的这些规律, 竟可能地选择带来高分的行为 (比如这里的开心脸). 这也就证明了在强化学习中, 分数标签就是他的老师, 他和监督学习中的老师也差不多.
方法汇总:
(1)Modelfree 和 Modelbased
Modelfree:不尝试去理解环境, 环境给了我们什么就是什么;方法有很多, 像 Q learning, Sarsa, Policy Gradients 都是从环境中得到反馈然后从中学习,机器人只能按部就班, 一步一步等待真实世界的反馈, 再根据反馈采取下一步行动。
Modelbased:model 就是用模型来表示环境, 那理解了环境也就是学会了用一个模型来代表环境;只是多了一道程序, 为真实世界建模, 也可以说他们都是 model-free 的强化学习, 只是 model-based 多出了一个虚拟环境, 我们不仅可以像 model-free 那样在现实中玩耍,还能在游戏中玩耍, 而玩耍的方式也都是 model-free 中那些玩耍方式, 最终 model-based 还有一个杀手锏是 model-free 超级羡慕的. 那就是想象力。他能通过想象来预判断接下来将要发生的所有情况. 然后选择这些想象情况中最好的那种. 并依据这种情况来采取下一步的策略。
(2)基于概率 和 基于价值
基于概率:强化学习中最直接的一种, 他能通过感官分析所处的环境, 直接输出下一步要采取的各种动作的概率, 然后根据概率采取行动, 所以每种动作都有可能被选中, 只是可能性不同。我们现在说的动作都是一个一个不连续的动作, 而对于选取连续的动作, 基于价值的方法是无能为力的. 我们却能用一个概率分布在连续动作中选取特定动作, 这也是基于概率的方法的优点之一。方法有:Policy Gradients
基于价值:输出则是所有动作的价值, 我们会根据最高价值来选着动作, 相比基于概率的方法, 基于价值的决策部分更为铁定, 毫不留情, 就选价值最高的, 而基于概率的, 即使某个动作的概率最高, 但是还是不一定会选到他.方法有: Q learning, Sarsa
我们还能结合这两类方法的优势之处, 创造更牛逼的一种方法, 叫做 Actor-Critic, actor 会基于概率做出动作, 而 critic 会对做出的动作给出动作的价值, 这样就在原有的 policy gradients 上加速了学习过程.
(3)回合更新 和 单步更新
回合更新:游戏开始后, 我们要等待游戏结束, 然后再总结这一回合中的所有转折点, 再更新我们的行为准则;
单步更新:在游戏进行中每一步都在更新, 不用等待游戏的结束, 这样我们就能边玩边学习了;因为单步更新更有效率, 所以现在大多方法都是基于单步更新. 比如有的强化学习问题并不属于回合问题.Qlearning, Sarsa, 升级版的 policy gradients 等都是单步更新制。
(4)在线学习和离线学习
在线学习:指我必须本人在场, 并且一定是本人边玩边学习,方法: Sarsa 了, 还有一种优化 Sarsa 的算法, 叫做 Sarsa lambda;
离线学习:你可以选择自己玩, 也可以选择看着别人玩, 通过看别人玩来学习别人的行为准则, 离线学习 同样是从过往的经验中学习, 但是这些过往的经历没必要是自己的经历, 任何人的经历都能被学习. 或者我也不必要边玩边学习, 我可以白天先存储下来玩耍时的记忆, 然后晚上通过离线学习来学习白天的记忆。方法:Q learning, 后来人也根据离线学习的属性, 开发了更强大的算法, 比如让计算机学会玩电动的 Deep-Q-Network.
1、Q-learning
(1)算法原理
假设现在我们处于写作业的状态而且我们以前并没有尝试过写作业时看电视, 所以现在我们有两种选择 , 1, 继续写作业, 2, 跑去看电视. 因为以前没有被罚过, 所以我选看电视, 然后现在的状态变成了看电视, 我又选了 继续看电视, 接着我还是看电视, 最后爸妈回家, 发现我没写完作业就去看电视了, 狠狠地惩罚了我一次, 我也深刻地记下了这一次经历, 并在我的脑海中将 “没写完作业就看电视” 这种行为更改为负面行为, 我们在看看 Q learning 根据很多这样的经历是如何来决策的吧.
假设我们的行为准则已经学习好了, 现在我们处于状态s1, 我在写作业, 我有两个行为 a1, a2, 分别是看电视和写作业, 根据我的经验, 在这种 s1 状态下, a2 写作业 带来的潜在奖励要比 a1 看电视高, 这里的潜在奖励我们可以用一个有关于 s 和 a 的 Q 表格代替, 在我的记忆Q表格中, Q(s1, a1)=-2 要小于 Q(s1, a2)=1, 所以我们判断要选择 a2 作为下一个行为. 现在我们的状态更新成 s2 , 我们还是有两个同样的选择, 重复上面的过程, 在行为准则Q 表中寻找 Q(s2, a1) Q(s2, a2) 的值, 并比较他们的大小, 选取较大的一个. 接着根据 a2 我们到达 s3 并在此重复上面的决策过程. Q learning 的方法也就是这样决策的.
(2)策略更新
所以我们回到之前的流程, 根据 Q 表的估计, 因为在 s1 中, a2 的值比较大, 通过之前的决策方法, 我们在 s1 采取了 a2, 并到达 s2, 这时我们开始更新用于决策的 Q 表, 接着我们并没有在实际中采取任何行为, 而是再想象自己在 s2 上采取了每种行为, 分别看看两种行为哪一个的 Q 值大, 比如说 Q(s2, a2) 的值比 Q(s2, a1) 的大, 所以我们把大的 Q(s2, a2) 乘上一个衰减值 gamma (比如是0.9) 并加上到达s2时所获取的奖励 R (这里还没有获取到我们的棒棒糖, 所以奖励为 0), 因为会获取实实在在的奖励 R , 我们将这个作为我现实中 Q(s1, a2) 的值, 但是我们之前是根据 Q 表估计 Q(s1, a2) 的值. 所以有了现实和估计值, 我们就能更新Q(s1, a2) , 根据 估计与现实的差距, 将这个差距乘以一个学习效率 alpha 累加上老的 Q(s1, a2) 的值 变成新的值. 但时刻记住, 我们虽然用 maxQ(s2) 估算了一下 s2 状态, 但还没有在 s2 做出任何的行为, s2 的行为决策要等到更新完了以后再重新另外做. 这就是 off-policy 的 Q learning 是如何决策和学习优化决策的过程.
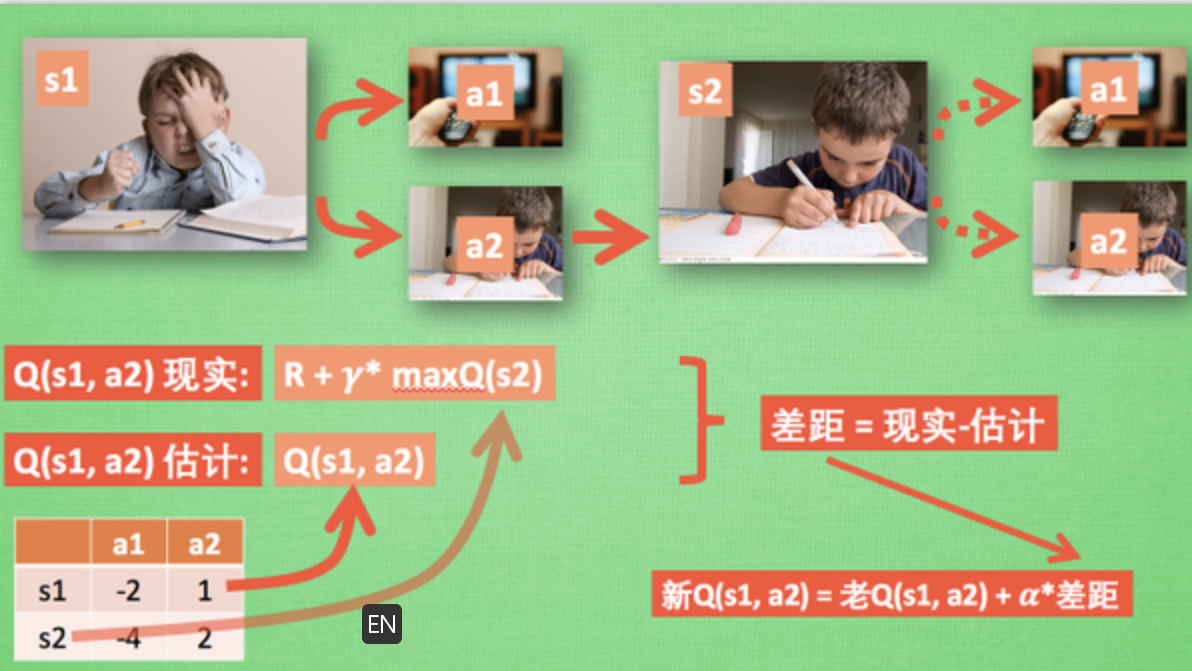
(3)整体算法

这一张图概括了我们之前所有的内容. 这也是 Q learning 的算法, 每次更新我们都用到了 Q 现实和 Q 估计, 而且 Q learning 的迷人之处就是 在 Q(s1, a2) 现实 中, 也包含了一个 Q(s2) 的最大估计值, 将对下一步的衰减的最大估计和当前所得到的奖励当成这一步的现实, 很奇妙吧. 最后我们来说说这套算法中一些参数的意义. Epsilon greedy 是用在决策上的一种策略, 比如 epsilon = 0.9 时, 就说明有90% 的情况我会按照 Q 表的最优值选择行为, 10% 的时间使用随机选行为. alpha是学习率, 来决定这次的误差有多少是要被学习的, alpha是一个小于1 的数. gamma 是对未来 reward 的衰减值. 我们可以这样想象.
公式中gamma的理解:为了让rl不仅看眼前利益,也看长远利益。
Q(s1) 是有关于之后所有的奖励, 但这些奖励正在衰减, 离 s1 越远的状态衰减越严重. 不好理解? 行, 我们想象 Qlearning 的机器人天生近视眼, gamma = 1 时, 机器人有了一副合适的眼镜, 在 s1 看到的 Q 是未来没有任何衰变的奖励, 也就是机器人能清清楚楚地看到之后所有步的全部价值, 但是当 gamma =0, 近视机器人没了眼镜, 只能摸到眼前的 reward, 同样也就只在乎最近的大奖励, 如果 gamma 从 0 变到 1, 眼镜的度数由浅变深, 对远处的价值看得越清楚, 所以机器人渐渐变得有远见, 不仅仅只看眼前的利益, 也为自己的未来着想.
(1)算法原理
我们使用表格来存储每一个状态 state, 和在这个 state 每个行为 action 所拥有的 Q 值. 而当今问题是在太复杂, 状态可以多到比天上的星星还多(比如下围棋). 如果全用表格来存储它们, 恐怕我们的计算机有再大的内存都不够, 而且每次在这么大的表格中搜索对应的状态也是一件很耗时的事. 不过, 在机器学习中, 有一种方法对这种事情很在行, 那就是神经网络. 我们可以将状态和动作当成神经网络的输入, 然后经过神经网络分析后得到动作的 Q 值, 这样我们就没必要在表格中记录 Q 值, 而是直接使用神经网络生成 Q 值. 还有一种形式的是这样, 我们也能只输入状态值, 输出所有的动作值, 然后按照 Q learning 的原则, 直接选择拥有最大值的动作当做下一步要做的动作. 我们可以想象, 神经网络接受外部的信息, 相当于眼睛鼻子耳朵收集信息, 然后通过大脑加工输出每种动作的值, 最后通过强化学习的方式选择动作.
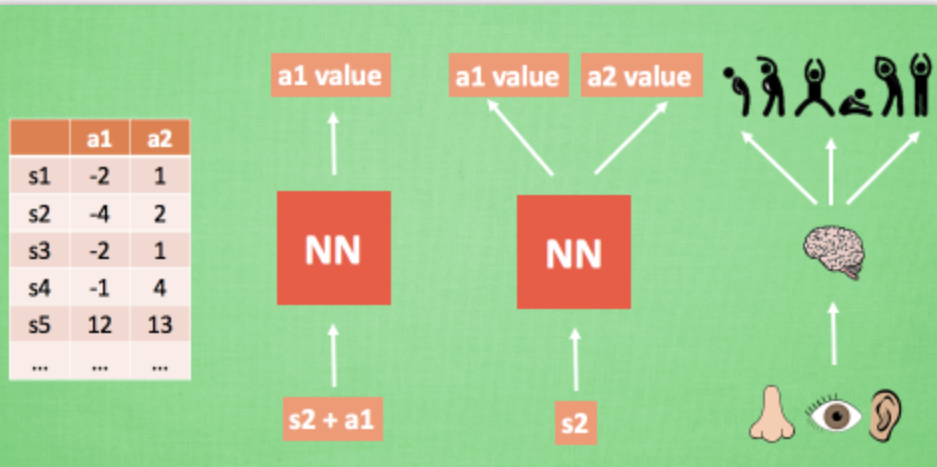
(2)策略更新
接下来我们基于第二种神经网络来分析, 我们知道, 神经网络是要被训练才能预测出准确的值. 那在强化学习中, 神经网络是如何被训练的呢? 首先, 我们需要 a1, a2 正确的Q值, 这个 Q 值我们就用之前在 Q learning 中的 Q 现实来代替. 同样我们还需要一个 Q 估计 来实现神经网络的更新. 所以神经网络的的参数就是老的 NN 参数 加学习率 alpha 乘以 Q 现实 和 Q 估计 的差距. 我们整理一下.
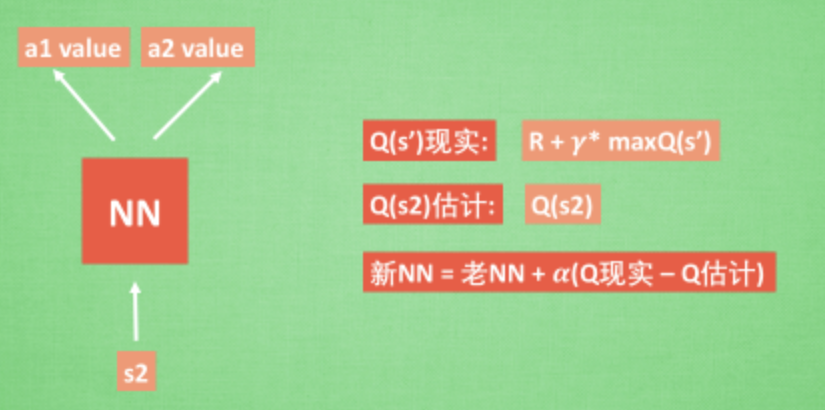
我们通过 NN 预测出Q(s2, a1) 和 Q(s2,a2) 的值, 这就是 Q 估计. 然后我们选取 Q 估计中最大值的动作来换取环境中的奖励 reward. 而 Q 现实中也包含从神经网络分析出来的两个 Q 估计值, 不过这个 Q 估计是针对于下一步在 s' 的估计. 最后再通过刚刚所说的算法更新神经网络中的参数. 但是这并不是 DQN 会玩电动的根本原因. 还有两大因素支撑着 DQN 使得它变得无比强大. 这两大因素就是 Experience replay 和 Fixed Q-targets.

(3)关键问题
简单来说, DQN 有一个记忆库用于学习之前的经历. 在之前的简介影片中提到过, Q learning 是一种 off-policy 离线学习法, 它能学习当前经历着的, 也能学习过去经历过的, 甚至是学习别人的经历. 所以每次 DQN 更新的时候, 我们都可以随机抽取一些之前的经历进行学习. 随机抽取这种做法打乱了经历之间的相关性, 也使得神经网络更新更有效率. Fixed Q-targets 也是一种打乱相关性的机理, 如果使用 fixed Q-targets, 我们就会在 DQN 中使用到两个结构相同但参数不同的神经网络, 预测 Q 估计 的神经网络具备最新的参数, 而预测 Q 现实 的神经网络使用的参数则是很久以前的. 有了这两种提升手段, DQN 才能在一些游戏中超越人类.

5、Policy Gradients
强化学习是一个通过奖惩来学习正确行为的机制. 家族中有很多种不一样的成员, 有学习奖惩值, 根据自己认为的高价值选行为, 比如 Q learning, Deep Q Network, 也有不通过分析奖励值, 直接输出行为的方法, 这就是今天要说的 Policy Gradients 了. 甚至我们可以为 Policy Gradients 加上一个神经网络来输出预测的动作.
(1)算法原理
对比起以值为基础的方法, Policy Gradients 直接输出动作的最大好处就是, 它能在一个连续区间内挑选动作, 而基于值的, 比如 Q-learning, 它如果在无穷多的动作中计算价值, 从而选择行为, 这, 它可吃不消. 有了神经网络当然方便, 但是, 我们怎么进行神经网络的误差反向传递呢? Policy Gradients 的误差又是什么呢? 答案是! 哈哈, 没有误差! 但是他的确是在进行某一种的反向传递. 这种反向传递的目的是让这次被选中的行为更有可能在下次发生. 但是我们要怎么确定这个行为是不是应当被增加被选的概率呢? 这时候我们的老朋友, reward 奖惩正可以在这时候派上用场。
观测的信息通过神经网络分析, 选出了左边的行为, 我们直接进行反向传递, 使之下次被选的可能性增加, 但是奖惩信息却告诉我们, 这次的行为是不好的, 那我们的动作可能性增加的幅度 随之被减低. 这样就能靠奖励来左右我们的神经网络反向传递. 我们再来举个例子, 假如这次的观测信息让神经网络选择了右边的行为, 右边的行为随之想要进行反向传递, 使右边的行为下次被多选一点, 这时, 奖惩信息也来了, 告诉我们这是好行为, 那我们就在这次反向传递的时候加大力度, 让它下次被多选的幅度更猛烈! 这就是 Policy Gradients 的核心思想了. 很简单吧.
优势:输出的这个 action 可以是一个连续的值, 之前我们说到的 value-based 方法输出的都是不连续的值, 然后再选择值最大的 action. 而 policy gradient 可以在一个连续分布上选取 action.
6、Actor Critic
强化学习中的一种结合体 Actor Critic (演员评判家), 它合并了 以值为基础 (比如 Q learning) 和 以动作概率为基础 (比如 Policy Gradients) 两类强化学习算法.
我们有了像 Q-learning 这么伟大的算法, 为什么还要瞎折腾出一个 Actor-Critic? 原来 Actor-Critic 的 Actor 的前生是 Policy Gradients, 这能让它毫不费力地在连续动作中选取合适的动作, 而 Q-learning 做这件事会瘫痪. 那为什么不直接用 Policy Gradients 呢? 原来 Actor Critic 中的 Critic 的前生是 Q-learning 或者其他的 以值为基础的学习法 , 能进行单步更新, 而传统的 Policy Gradients 则是回合更新, 这降低了学习效率.
现在我们有两套不同的体系, Actor 和 Critic, 他们都能用不同的神经网络来代替 . 在 Policy Gradients 的影片中提到过, 现实中的奖惩会左右 Actor 的更新情况. Policy Gradients 也是靠着这个来获取适宜的更新. 那么何时会有奖惩这种信息能不能被学习呢? 这看起来不就是 以值为基础的强化学习方法做过的事吗. 那我们就拿一个 Critic 去学习这些奖惩机制, 学习完了以后. 由 Actor 来指手画脚, 由 Critic 来告诉 Actor 你的那些指手画脚哪些指得好, 哪些指得差, Critic 通过学习环境和奖励之间的关系, 能看到现在所处状态的潜在奖励, 所以用它来指点 Actor 便能使 Actor 每一步都在更新, 如果使用单纯的 Policy Gradients, Actor 只能等到回合结束才能开始更新.
但是事物终有它坏的一面, Actor-Critic 涉及到了两个神经网络, 而且每次都是在连续状态中更新参数, 每次参数更新前后都存在相关性, 导致神经网络只能片面的看待问题, 甚至导致神经网络学不到东西. Google DeepMind 为了解决这个问题, 修改了 Actor Critic 的算法,将之前在电动游戏 Atari 上获得成功的 DQN 网络加入进 Actor Critic 系统中, 这种新算法叫做 Deep Deterministic Policy Gradient, 成功的解决的在连续动作预测上的学不到东西问题. 所以之后, 我们再来说说什么是这种高级版本的 Deep Deterministic Policy Gradient 吧.
(1)算法原理
结合了 Policy Gradient (Actor) 和 Function Approximation (Critic) 的方法. Actor 基于概率选行为, Critic 基于 Actor 的行为评判行为的得分, Actor 根据 Critic 的评分修改选行为的概率.
Actor Critic 方法的优势: 可以进行单步更新, 比传统的 Policy Gradient 要快.
Actor Critic 方法的劣势: 取决于 Critic 的价值判断, 但是 Critic 难收敛, 再加上 Actor 的更新, 就更难收敛. 为了解决收敛问题, Google Deepmind 提出了 Actor Critic 升级版 Deep Deterministic Policy Gradient. 后者融合了 DQN 的优势, 解决了收敛难的问题。

Actor 在运用 Policy Gradient 的方法进行 Gradient ascent 的时候, 由 Critic 来告诉他, 这次的 Gradient ascent 是不是一次正确的 ascent, 如果这次的得分不好, 那么就不要 ascent 那么多.
(2)策略更新
详见教程:代码 & github
7、Deep Deterministic Policy Gradient (DDPG)
它吸收了 Actor-Critic 让 Policy gradient 单步更新的精华, 而且还吸收让计算机学会玩游戏的 DQN 的精华, 合并成了一种新算法, 叫做 Deep Deterministic Policy Gradient. 那 DDPG 到底是什么样的算法呢, 我们就拆开来分析, 我们将 DDPG 分成 ‘Deep’ 和 ‘Deterministic Policy Gradient’, 然后 ‘Deterministic Policy Gradient’ 又能被细分为 ‘Deterministic’ 和 ‘Policy Gradient’.
我们在 DQN 的影片当中提到过, 使用一个记忆库和两套结构相同, 但参数更新频率不同的神经网络能有效促进学习. 那我们也把这种思想运用到 DDPG 当中, 使 DDPG 也具备这种优良形式. 但是 DDPG 的神经网络形式却比 DQN 的要复杂一点点.
(1)算法原理
它其实和我们之前提到的 Actor-Critic 形式差不多, 也需要有基于 策略 Policy 的神经网络 和基于 价值 Value 的神经网络, 但是为了体现 DQN 的思想, 每种神经网络我们都需要再细分为两个, Policy Gradient 这边, 我们有估计网络和现实网络, 估计网络用来输出实时的动作, 供 actor 在现实中实行. 而现实网络则是用来更新价值网络系统的. 所以我们再来看看价值系统这边, 我们也有现实网络和估计网络, 他们都在输出这个状态的价值, 而输入端却有不同, 状态现实网络这边会拿着从动作现实网络来的动作加上状态的观测值加以分析, 而状态估计网络则是拿着当时 Actor 施加的动作当做输入.在实际运用中, DDPG 的这种做法的确带来了更有效的学习过程.
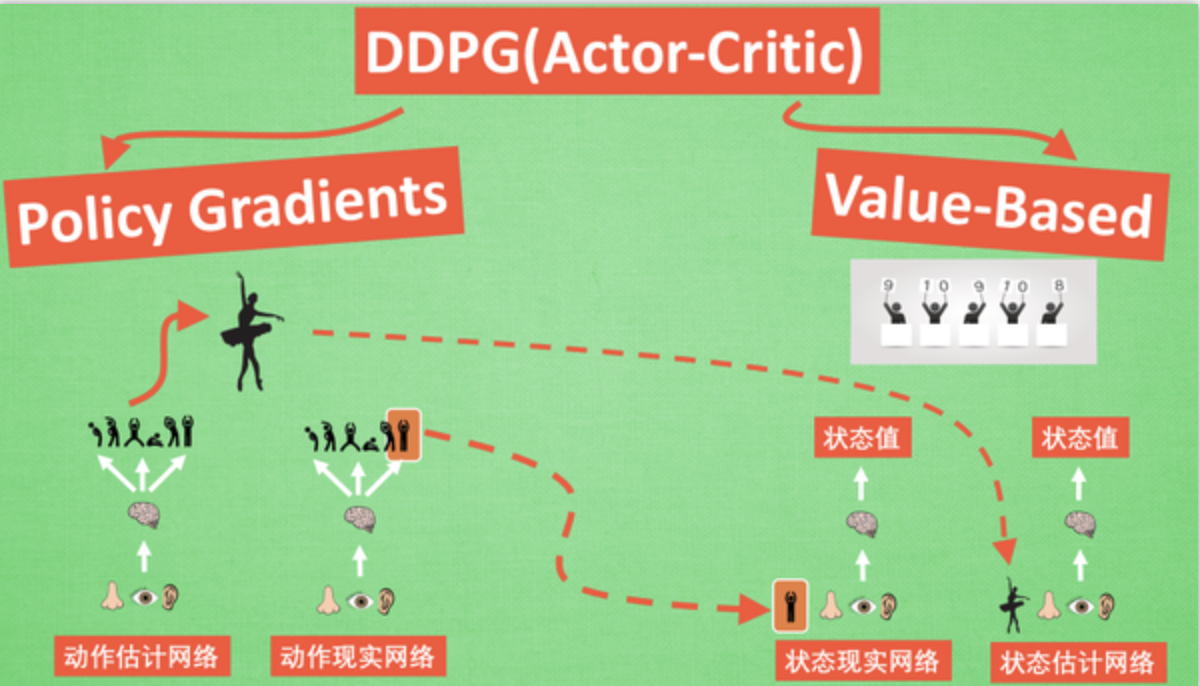
一句话概括 DDPG: Google DeepMind 提出的一种使用 Actor Critic 结构, 但是输出的不是行为的概率, 而是具体的行为, 用于连续动作 (continuous action) 的预测. DDPG 结合了之前获得成功的 DQN 结构, 提高了 Actor Critic 的稳定性和收敛性.
(2)策略迭代

关于 Actor 部分, 他的参数更新同样会涉及到 Critic, 上面是关于 Actor 参数的更新, 它的前半部分 grad[Q] 是从 Critic 来的, 这是在说: 这次 Actor 的动作要怎么移动, 才能获得更大的 Q, 而后半部分 grad[u] 是从 Actor 来的, 这是在说: Actor 要怎么样修改自身参数, 使得 Actor 更有可能做这个动作. 所以两者合起来就是在说: Actor 要朝着更有可能获取大 Q 的方向修改动作参数了.
![]()
上面这个是关于 Critic 的更新, 它借鉴了 DQN 和 Double Q learning 的方式, 有两个计算 Q 的神经网络, Q_target 中依据下一状态, 用 Actor 来选择动作, 而这时的 Actor 也是一个 Actor_target (有着 Actor 很久之前的参数). 使用这种方法获得的 Q_target 能像 DQN 那样切断相关性, 提高收敛性.
网络结构:
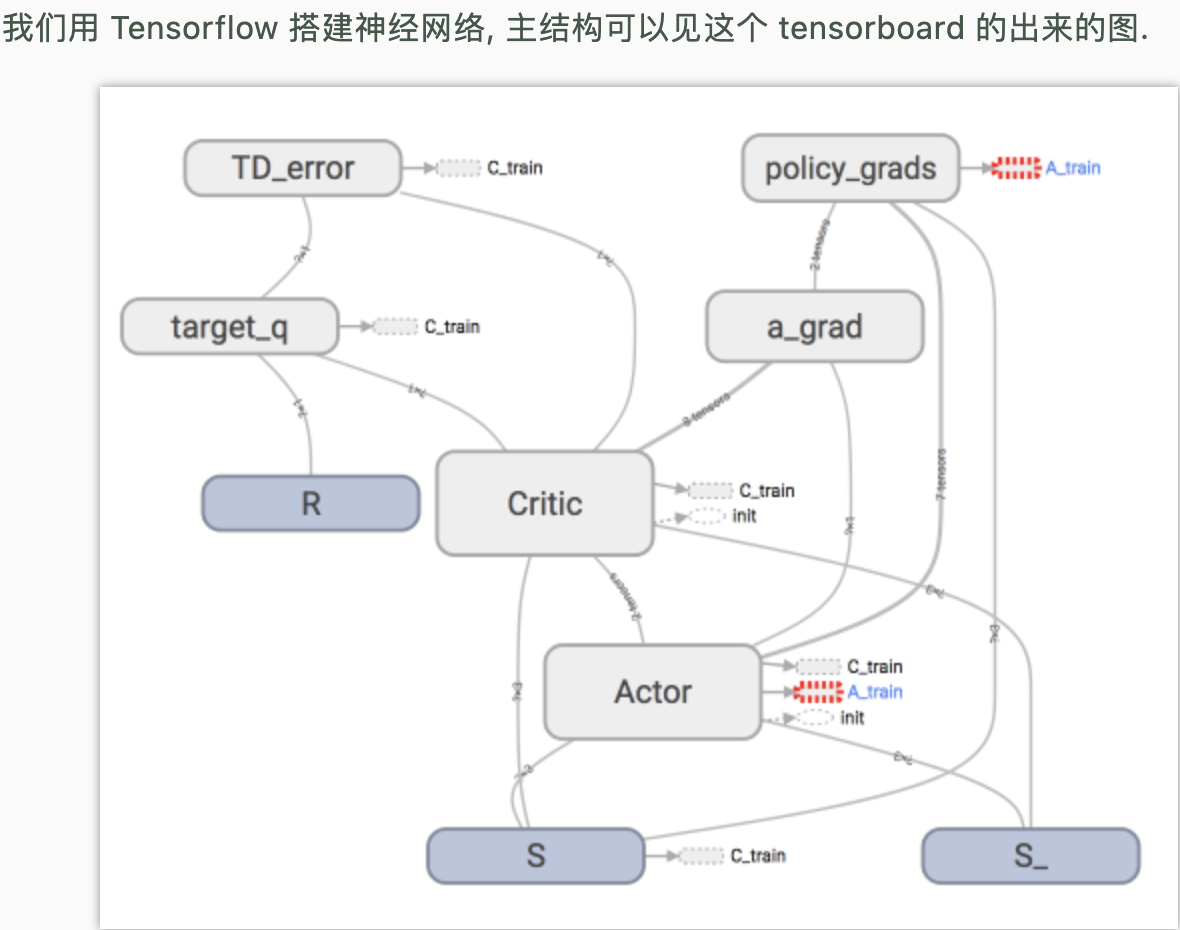
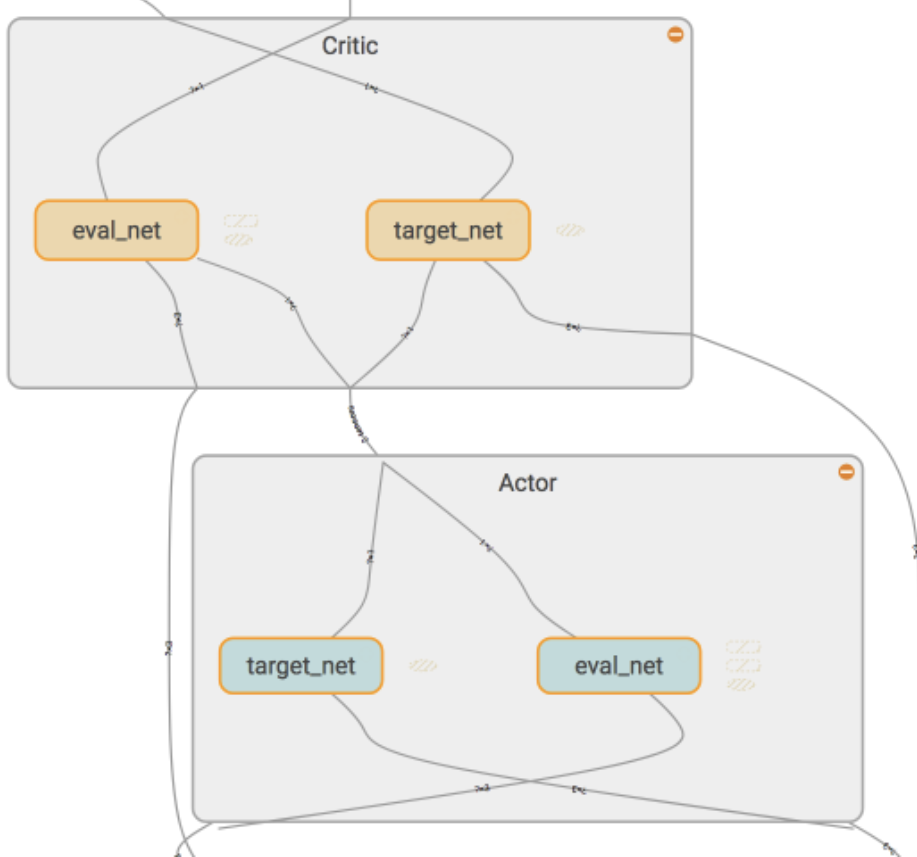
具体实现代码:莫烦代码库
参考文献:
1、莫烦课程
2、CSDN相关讲解



 浙公网安备 33010602011771号
浙公网安备 33010602011771号