代码题（68）— 跳跃游戏、合并区间、盛最多水的容器

1、55. 跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

　　这里可以用动态规划 Dynamic Programming 来解，维护一个一维数组 dp，其中 dp[i] 表示达到i位置时剩余的跳力，若到达某个位置时跳力为负了，说明无法到达该位置。接下来难点就是推导状态转移方程啦，想想啊，到达当前位置的剩余跳力跟什么有关呢，其实是跟上一个位置的剩余跳力（dp 值）和上一个位置新的跳力（nums 数组中的值）有关，这里新的跳力就是原数组中每个位置的数字，因为其代表了以当前位置为起点能到达的最远位置。所以当前位置的剩余跳力（dp 值）和当前位置新的跳力中的较大那个数决定了当前能到的最远距离，而下一个位置的剩余跳力（dp 值）就等于当前的这个较大值减去1，因为需要花一个跳力到达下一个位置，所以就有状态转移方程了：dp[i] = max(dp[i - 1], nums[i - 1]) - 1，如果当某一个时刻 dp 数组的值为负了，说明无法抵达当前位置，则直接返回 false，最后循环结束后直接返回 true  即可.

class Solution {
public:
    bool canJump(vector<int>& nums) {
        if(nums.empty())
            return false;
        vector<int> dp(nums.size(), 0);
        for(int i=1;i<nums.size();++i){
            dp[i] = max(dp[i-1], nums[i-1]) - 1;
            if(dp[i] < 0)
                return false;
        }
        return true;
    }
};

2、56. 合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

将起始位置和结束位置分别存到了两个不同的数组 starts 和 ends 中，然后分别进行排序，之后用两个指针i和j，初始化时分别指向 starts 和 ends 数组的首位置，然后如果i指向 starts 数组中的最后一个位置，或者当 starts 数组上 i+1 位置上的数字大于 ends 数组的i位置上的数时，此时说明区间已经不连续了，我们来看题目中的例子，排序后的 starts 和 ends 为：

starts:    1    2    8    15

ends:     3    6    10    18

红色为i的位置，蓝色为j的位置，那么此时 starts[i+1] 为8，ends[i] 为6，8大于6，所以此时不连续了，将区间 [starts[j], ends[i]]，即 [1, 6] 加入结果 res 中，然后j赋值为 i+1 继续循环，参见代码如下：

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        int n = intervals.size();
        vector<vector<int>> res;
        if (n <=0) return res;
        vector<int> starts, ends;
        for(int i=0;i<n;++i){
            starts.push_back(intervals[i][0]);
            ends.push_back(intervals[i][1]);
        }
        sort(starts.begin(), starts.end());
        sort(ends.begin(), ends.end());
        for(int i=0, j=0;i<n;++i){
            if(i == n-1 || starts[i+1] > ends[i]){
                res.push_back({starts[j], ends[i]});
                j = i+1;
            }
        }
        return res;
    }
};

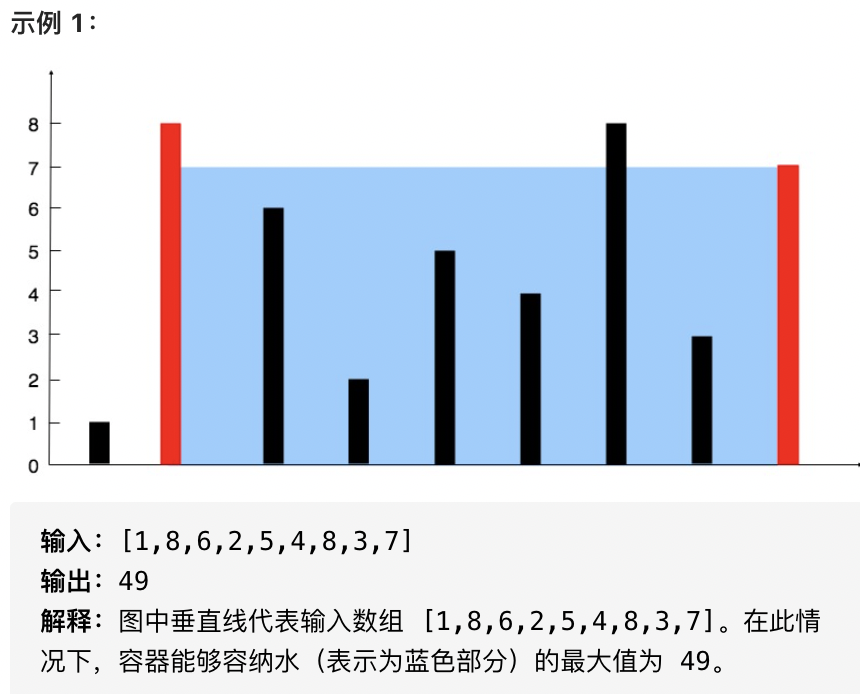
 3、11. 盛最多水的容器

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.empty())
            return 0;
        int i=0, j=height.size()-1;
        int res = 0;
        while(i<j){
            int h = min(height[i], height[j]);
            res = max(res, h*(j-i));
            if(height[i] < height[j])
                i++;
            else 
                j--;
        }
        return res;
    }
};