机器学习第二次作业
机器学习第二次作业
又到了说题外话的时候,感觉学的东西和代码实现有点脱节。不过整体代码实现完,发现自己对分类器包括公式有了更深的理解。
题目1,2
1. Iris数据集已与常见的机器学习工具集成,请查阅资料找出MATLAB平台或Python平台加载内置Iris数据集方法,并简要描述该数据集结构。
2. Iris数据集中有一个种类与另外两个类是线性可分的,其余两个类是线性不可分的。请你通过数据可视化的方法找出该线性可分类并给出判断依据。
代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
#白化函数
def zca_whitening(inputs):
sigma = np.dot(inputs, inputs.T)/inputs.shape[1] #inputs是经过归一化处理的,所以这边就相当于计算协方差矩阵
U,S,V = np.linalg.svd(sigma) #奇异分解
epsilon = 0.1 #白化的时候,防止除数为0
ZCAMatrix = np.dot(np.dot(U, np.diag(1.0/np.sqrt(np.diag(S) + epsilon))), U.T) #计算zca白化矩阵
return np.dot(ZCAMatrix, inputs) #白化变换
iris = load_iris() # 加载机器学习的下的iris数据集,先来认识一下iris数据集的一些操作,其实iris数据集就是一个字典集。下面注释的操作,可以帮助理解
#调用白化函数
print(iris.keys()) # 打印iris索引,关键字
n_sample, n_features = iris.data.shape
print(iris.data.shape[0]) # 样本
print(iris.data.shape[1]) # 4个特征
#
#print(n_sample, n_features)
#
print(iris.data[0])
#
print(ir代码is.target.shape)
print(iris.target) # 三个种类,分别用0,1,2来表示
print(iris.target_names) # 三个种类的英文名称
print("feature_names:", iris.feature_names)
# iris_setosa = zca_whitening(iris.data[:50]) # 第一种花的数据
# iris_versicolor = zca_whitening(iris.data[50:100]) # 第二种花的数据
# iris_virginica = zca_whitening(iris.data[100:150]) # 第三种花的数据
iris_setosa = iris.data[:50] # 第一种花的数据
iris_versicolor = iris.data[50:100] # 第二种花的数据
iris_virginica = iris.data[100:150] # 第三种花的数据
iris_setosa = np.hsplit(iris_setosa, 4) # 运用numpy.hsplit水平分割获取各特征集合,分割成四列
iris_versicolor = np.hsplit(iris_versicolor, 4)
iris_virginica = np.hsplit(iris_virginica, 4)
size = 5 # 散点的大小
setosa_color = 'b' # 蓝色代表setosa
versicolor_color = 'g' # 绿色代表versicolor
virginica_color = 'r' # 红色代表virginica
label_text = ['Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width']
# print(ticks)
plt.figure(figsize=(12, 12)) # 设置画布大小
plt.suptitle("Iris Set (blue=setosa, green=versicolour, red=virginca) ", fontsize=30)
for i in range(0, 4):
for j in range(0, 4):
plt.subplot(4, 4, i * 4 + j + 1) # 创建子画布
if i == j:
print(i*4+j+1) #序列号
plt.xticks([])
plt.yticks([])
plt.text(0.1, 0.4, label_text[i], size=18)
else:
plt.scatter(iris_setosa[j], iris_setosa[i], c=setosa_color, s=size)
plt.scatter(iris_versicolor[j], iris_versicolor[i], c=versicolor_color, s=size)
plt.scatter(iris_virginica[j], iris_virginica[i], c=virginica_color, s=size)
plt.show()
结果截图
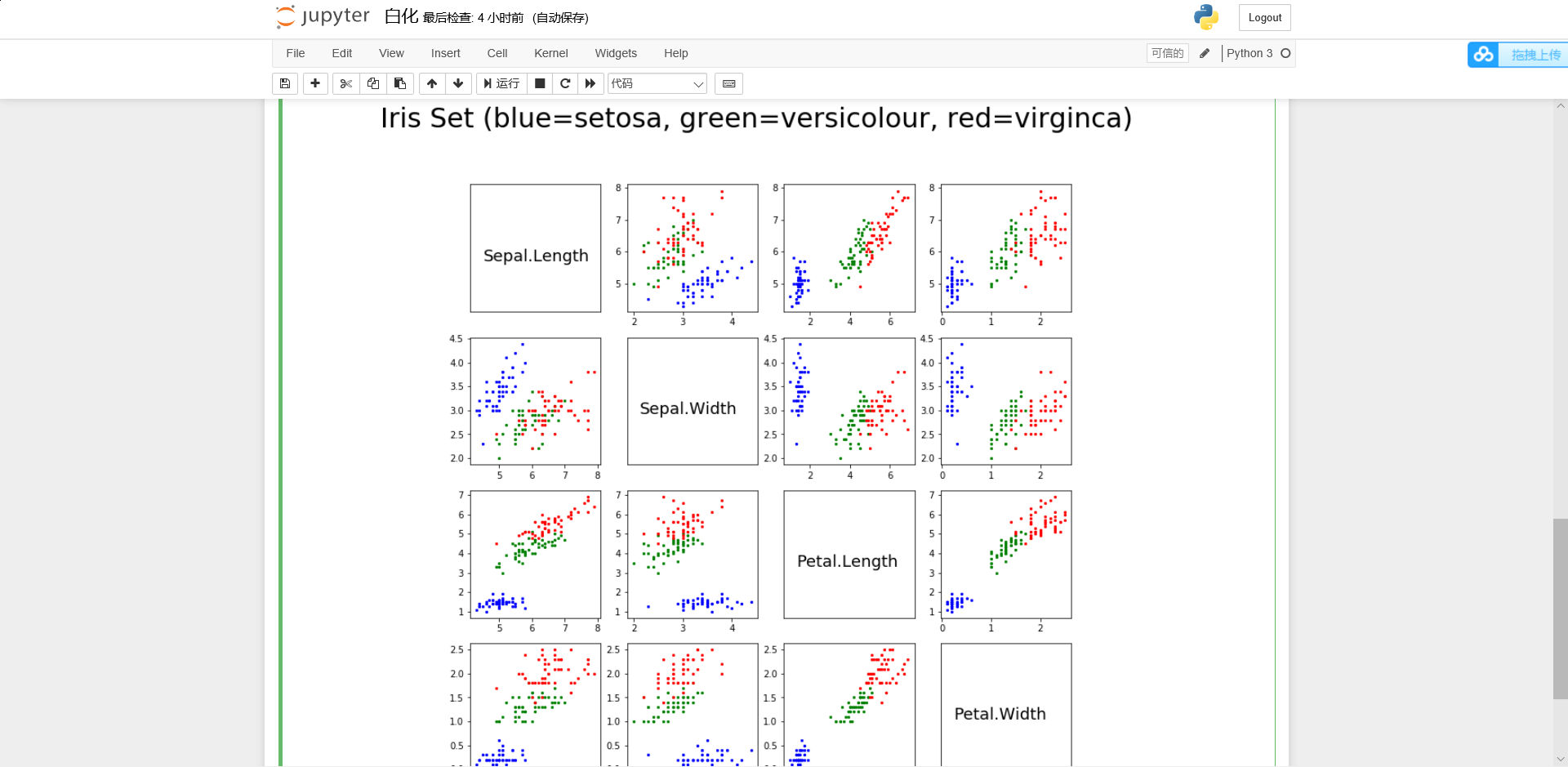
题目4
将Iris数据集白化,可视化白化结果并于原始可视化结果比较,讨论白化的作用。
代码
#白化函数
def zca_whitening(inputs):
sigma = np.dot(inputs, inputs.T)/inputs.shape[1] #inputs是经过归一化处理的,所以这边就相当于计算协方差矩阵
U,S,V = np.linalg.svd(sigma) #奇异分解
epsilon = 0.1 #白化的时候,防止除数为0
ZCAMatrix = np.dot(np.dot(U, np.diag(1.0/np.sqrt(np.diag(S) + epsilon))), U.T) #计算zca白化矩阵
return np.dot(ZCAMatrix, inputs) #白化变换
iris_setosa = zca_whitening(iris.data[:50]) # 第一种花的数据
iris_versicolor = zca_whitening(iris.data[50:100]) # 第二种花的数据
iris_virginica = zca_whitening(iris.data[100:150]) # 第三种花的数据
结果图片

结论通过对比图片,可以得到白化的作用主要是对数据进行降维
题目3
去除Iris数据集中线性不可分的类中最后一个,余下的两个线性可分的类构成的数据集命令为Iris_linear,请使用留出法将Iris_linear数据集按7:3分为训练集与测试集,并使用训练集训练一个MED分类器,在测试集上测试训练好的分类器的性能,给出《模式识别与机器学习-评估方法与性能指标》中所有量化指标并可视化分类结果。
代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import random
iris = load_iris() # 加载机器学习的下的iris数据集,先来认识一下iris数据集的一些操作,其实iris数据集就是一个字典集。下面注释的操作,可以帮助理解
Iris_linear = iris.data[:100] #线性可分的数据
iris_setosa = iris.data[:50] # 第一种花的数据
iris_versicolor = iris.data[50:100] # 第二种花的数据
def split_train(data,test_ratio):#随机划分数据集
shuffled_indices=np.random.permutation(len(data))
test_set_size=int(len(data)*test_ratio)
test_indices =shuffled_indices[:test_set_size]
train_indices=shuffled_indices[test_set_size:]
return data[train_indices],data[test_indices]
def eucldist(coords1, coords2):#求两点欧式距离
dist = 0
for (x, y) in zip(coords1, coords2):
dist += (x - y)**2
return dist**0.5
split = split_train(iris_setosa,0.3)
iris_setosa_train = split[0]#size35
iris_setosa_text = split[1]
split = split_train(iris_versicolor,0.3)
iris_versicolor_train = split[0]#size35
iris_versicolor_text = split[1]
class1 = []
#print(iris_setosa_train)
for j in range(0,4):
sum = 0
for i in range(0,35):
sum = sum + iris_setosa_train[i][j]
class1.append(sum/35)
print(class1)
class2 = []
#print(iris_versicolor_train)
for j in range(0,4):
sum = 0
for i in range(0,35):
sum = sum + iris_versicolor_train[i][j]
class2.append(sum/35)
print(class2)
for i in range (0,15):
if (eucldist(iris_setosa_text[i], class1)<eucldist(iris_setosa_text[i], class2)):
print("true")
else:
print("falus")
for i in range (0,15):
if (eucldist(iris_versicolor_text[i], class2)<eucldist(iris_versicolor_text[i], class1)):
print("true")
else:
print("falus")
versicolor_color = 'g' # 绿色代表versicolor
setosa_color = 'r' # 红色代表virginica
size = 5 # 散点的大小
plt.figure(figsize=(12, 12)) # 设置画布大小
x=np.linspace(5,7,50)
for i in range(0,15):
plt.scatter(iris_setosa_text[i][0], iris_setosa_text[i][0], c=setosa_color, s=size)
plt.scatter(iris_versicolor_text[i][0],iris_versicolor_text[i][0], c=versicolor_color, s=size)
plt.plot(x,-(class1[0]-class2[0])/(class1[1]-class2[1])*x+(class1[1]+class2[1])/2+(class1[0]-class2[0])/(class1[1]-class2[1])*(class1[0]-class2[0])/2)
plt.show()
结果图片
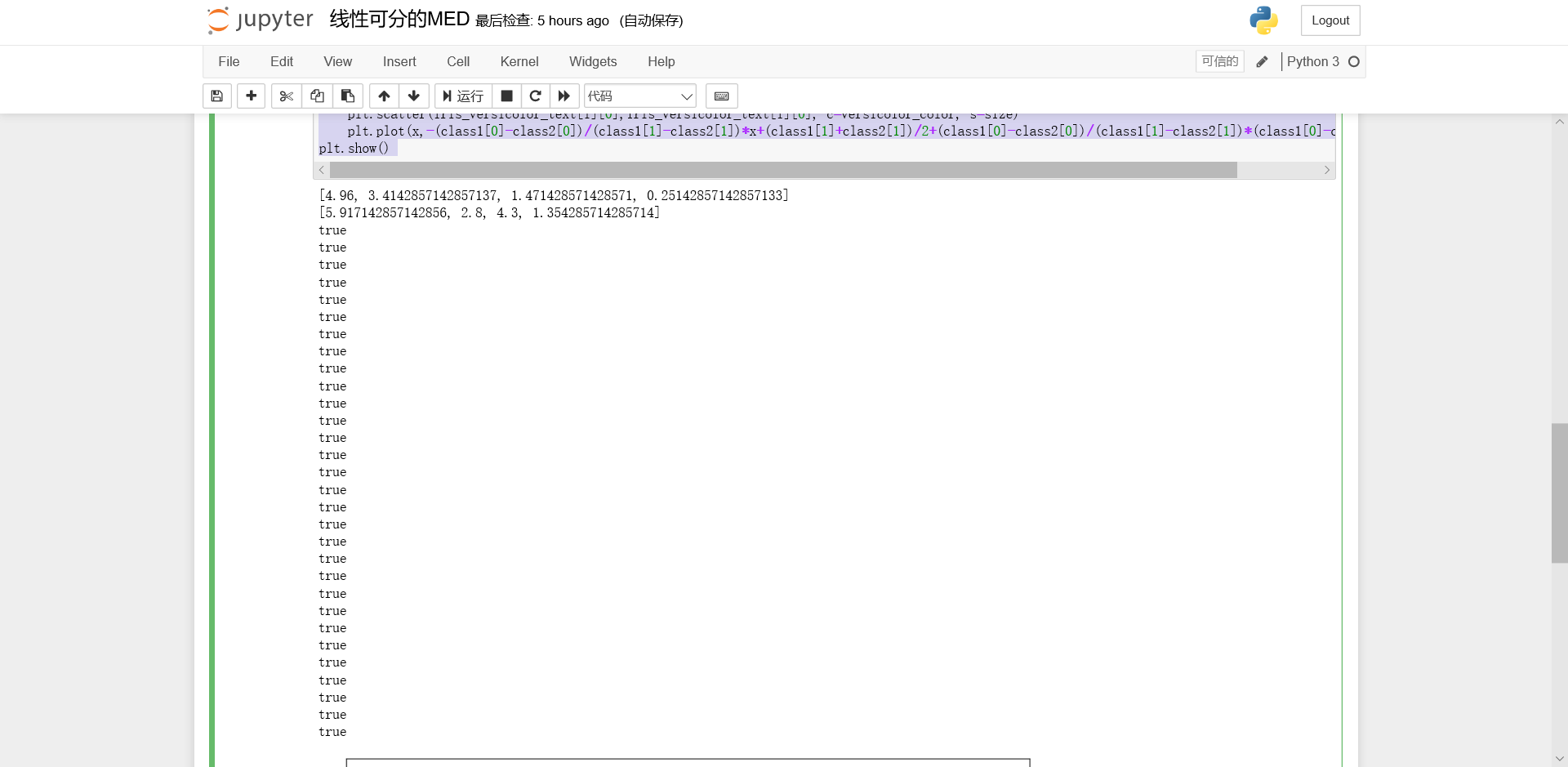
运行结果
Accuracy为100%
题目5
题目
去除Iris数据集中线性可分的类,余下的两个线性不可分的类构成的数据集命令为Iris_nonlinear,请使用留出法将Iris_nonlinear数据集按7:3分为训练集与测试集,并使用训练集训练一个MED分类器,在测试集上测试训练好的分类器的性能,给出《模式识别与机器学习-评估方法与性能指标》中所有量化指标并可视化分类结果。讨论本题结果与3题结果的差异。
代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import random
iris = load_iris() # 加载机器学习的下的iris数据集,先来认识一下iris数据集的一些操作,其实iris数据集就是一个字典集。下面注释的操作,可以帮助理解
Iris_linear = iris.data[:100] #线性可分的数据
#print(Iris_linear)
iris_setosa = iris.data[50:100] # 第一种花的数据
iris_versicolor = iris.data[100:150] # 第二种花的数据
def split_train(data,test_ratio):#随机划分数据集
shuffled_indices=np.random.permutation(len(data))
test_set_size=int(len(data)*test_ratio)
test_indices =shuffled_indices[:test_set_size]
train_indices=shuffled_indices[test_set_size:]
return data[train_indices],data[test_indices]
def eucldist(coords1, coords2):#求两点欧式距离
dist = 0
for (x, y) in zip(coords1, coords2):
dist += (x - y)**2
return dist**0.5
#print(Iris_linear)
split = split_train(iris_setosa,0.3)
iris_setosa_train = split[0]#size35
iris_setosa_text = split[1]
split = split_train(iris_versicolor,0.3)
iris_versicolor_train = split[0]#size35
iris_versicolor_text = split[1]
class1 = []
#print(iris_setosa_train)
for j in range(0,4):
sum = 0
for i in range(0,35):
sum = sum + iris_setosa_train[i][j]
class1.append(sum/35)
print(class1)
class2 = []
#print(iris_versicolor_train)
for j in range(0,4):
sum = 0
for i in range(0,35):
sum = sum + iris_versicolor_train[i][j]
class2.append(sum/35)
print(class2)
for i in range (0,15):
if (eucldist(iris_setosa_text[i], class1)<eucldist(iris_setosa_text[i], class2)):
print("true")
else:
print("falus")
for i in range (0,15):
if (eucldist(iris_versicolor_text[i], class2)<eucldist(iris_versicolor_text[i], class1)):
print("true")
else:
print("falus")
setosa_color = 'g' # 绿色代表versicolor
virginica_color = 'r' # 红色代表virginica
size = 5 # 散点的大小
plt.figure(figsize=(12, 12)) # 设置画布大小
x=np.linspace(5,7,50)
for i in range(0,15):
plt.scatter(iris_setosa_text[i][0], iris_setosa_text[i][0], c=setosa_color, s=size)
plt.scatter(iris_versicolor_text[i][0],iris_versicolor_text[i][0], c=virginica_color, s=size)
plt.plot(x,-(class2[0]-class1[0])/(class2[1]-class1[1])*x+(class2[1]+class1[1])/2+(class2[0]-class1[0])/(class2[1]-class1[1])*(class2[0]-class1[0])/2)
plt.show()
结果截图
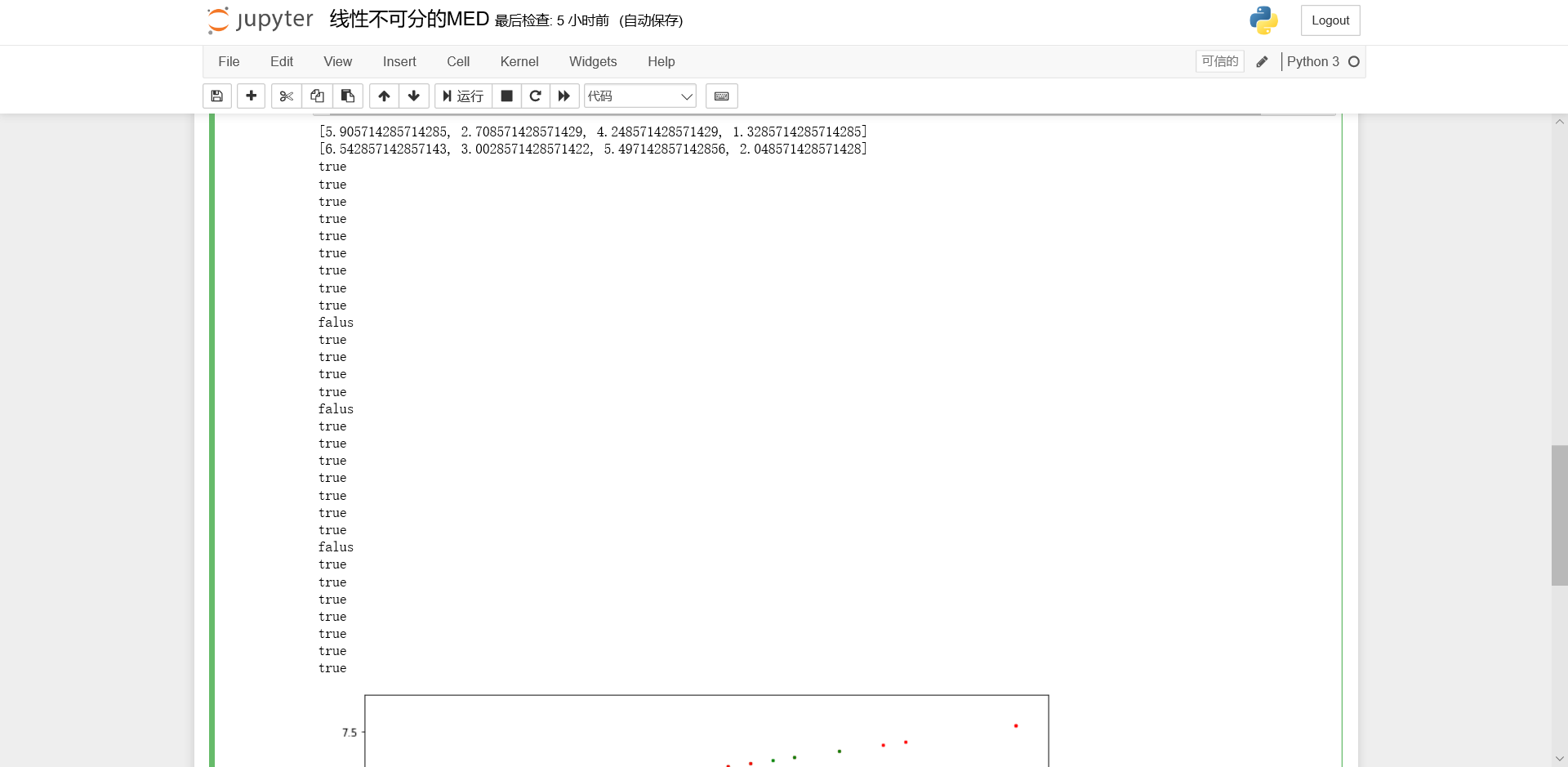
运行结果
Accuracy为90%
题目6
题目
请使用5折交叉验证为Iris数据集训练一个多分类的贝叶斯分类器。给出平均Accuracy,并可视化实验结果。与第3题和第5题结果做比较,讨论贝叶斯分类器的优劣。
#贝叶斯分类器,使用贝叶斯公式。
#将每种样本进行5折交叉验证,先验概率相同
#所以后验概率与观测似然概率成正比,只需比较观测似然概率即可得到结果
#且决策风险定位相同
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import math
def calculateProb(x,mean,var):
exponent = math.exp(math.pow((x-mean),2)/(-2*var))
p = (1/math.sqrt(2*math.pi*var))*exponent
return p
iris = load_iris().data # 加载机器学习的下的iris数据集
iris_setosa = iris[0:50]
iris_versicolor = iris[50:100]
iris_virginica = iris[100:150]
countT = 1
countF = 1
for i in range(0,5):#5折交叉验证
iris_setosa_train = np.vstack((iris_setosa[0:i*10],iris_setosa[10*(i+1):50]))
iris_setosa_text = iris_setosa[i*10:10*(i+1)]
iris_versicolor_train = np.vstack((iris_versicolor[0:i*10],iris_versicolor[10*(i+1):50]))
iris_versicolor_text = iris_versicolor[i*10:10*(i+1)]
iris_virginica_train = np.vstack((iris_virginica[0:i*10],iris_virginica[10*(i+1):50]))
iris_virginica_text = iris_virginica[i*10:10*(i+1)]
#分割处理
iris_setosa_train = np.hsplit(iris_setosa_train, 4) # 运用numpy.hsplit水平分割获取各特征集合,分割成四列
iris_versicolor_train = np.hsplit(iris_versicolor, 4)
iris_virginica_train = np.hsplit(iris_virginica, 4)
#求均值
iris_setosa_train_mean = []
iris_versicolor_train_mean = []
iris_virginica_train_mean = []
for j in range(0,4):
iris_setosa_train_mean.append(np.mean(iris_setosa_train[j]))
for j in range(0,4):
iris_versicolor_train_mean.append(np.mean(iris_versicolor_train[j]))
for j in range(0,4):
iris_virginica_train_mean.append(np.mean(iris_virginica_train[j]))
#求方差
iris_setosa_train_var = []
iris_versicolor_train_var = []
iris_virginica_train_var = []
for j in range(0,4):
iris_setosa_train_var.append(np.var(iris_setosa_train[j]))
for j in range(0,4):
iris_versicolor_train_var.append(np.var(iris_versicolor_train[j]))
for j in range(0,4):
iris_virginica_train_var.append(np.var(iris_virginica_train[j]))
#求观测似然概率,使用setosa验证集验证
for j in range(0,10):
iris_setosa_setosa_prob = calculateProb(iris_setosa_text[j][0],iris_setosa_train_mean[0],iris_setosa_train_var[0])\
*calculateProb(iris_setosa_text[j][1],iris_setosa_train_mean[1],iris_setosa_train_var[1])\
*calculateProb(iris_setosa_text[j][2],iris_setosa_train_mean[2],iris_setosa_train_var[2])\
*calculateProb(iris_setosa_text[j][3],iris_setosa_train_mean[3],iris_setosa_train_var[3])
iris_setosa_versicolor_prob = calculateProb(iris_setosa_text[j][0],iris_versicolor_train_mean[0],iris_versicolor_train_var[0])\
*calculateProb(iris_setosa_text[j][1],iris_versicolor_train_mean[1],iris_versicolor_train_var[1])\
*calculateProb(iris_setosa_text[j][2],iris_versicolor_train_mean[2],iris_versicolor_train_var[2])\
*calculateProb(iris_setosa_text[j][3],iris_versicolor_train_mean[3],iris_versicolor_train_var[3])
iris_setosa_virginica_prob = calculateProb(iris_setosa_text[j][0],iris_virginica_train_mean[0],iris_virginica_train_var[0])\
*calculateProb(iris_setosa_text[j][1],iris_virginica_train_mean[1],iris_virginica_train_var[1])\
*calculateProb(iris_setosa_text[j][2],iris_virginica_train_mean[2],iris_virginica_train_var[2])\
*calculateProb(iris_setosa_text[j][3],iris_virginica_train_mean[3],iris_virginica_train_var[3])
if (iris_setosa_setosa_prob>iris_setosa_versicolor_prob and iris_setosa_setosa_prob>iris_setosa_virginica_prob):
print("true")
print(countT)
countT = countT + 1
else:
print("falus")
print(countF)
countF = countF + 1
print(iris_setosa_setosa_prob)
print(iris_setosa_versicolor_prob)
print(iris_setosa_virginica_prob)
#使用versicolor验证集验证
for j in range(0,10):
iris_versicolor_setosa_prob = calculateProb(iris_versicolor_text[j][0],iris_setosa_train_mean[0],iris_setosa_train_var[0])\
*calculateProb(iris_versicolor_text[j][1],iris_setosa_train_mean[1],iris_setosa_train_var[1])\
*calculateProb(iris_versicolor_text[j][2],iris_setosa_train_mean[2],iris_setosa_train_var[2])\
*calculateProb(iris_versicolor_text[j][3],iris_setosa_train_mean[3],iris_setosa_train_var[3])
iris_versicolor_versicolor_prob = calculateProb(iris_versicolor_text[j][0],iris_versicolor_train_mean[0],iris_versicolor_train_var[0])\
*calculateProb(iris_versicolor_text[j][1],iris_versicolor_train_mean[1],iris_versicolor_train_var[1])\
*calculateProb(iris_versicolor_text[j][2],iris_versicolor_train_mean[2],iris_versicolor_train_var[2])\
*calculateProb(iris_versicolor_text[j][3],iris_versicolor_train_mean[3],iris_versicolor_train_var[3])
iris_versicolor_virginica_prob = calculateProb(iris_versicolor_text[j][0],iris_virginica_train_mean[0],iris_virginica_train_var[0])\
*calculateProb(iris_versicolor_text[j][1],iris_virginica_train_mean[1],iris_virginica_train_var[1])\
*calculateProb(iris_versicolor_text[j][2],iris_virginica_train_mean[2],iris_virginica_train_var[2])\
*calculateProb(iris_versicolor_text[j][3],iris_virginica_train_mean[3],iris_virginica_train_var[3])
if (iris_versicolor_versicolor_prob>iris_versicolor_setosa_prob and iris_versicolor_versicolor_prob>iris_versicolor_virginica_prob):
print("true")
print(countT)
countT = countT + 1
else:
print("falus")
print(countF)
countF = countF + 1
print(iris_setosa_setosa_prob)
print(iris_setosa_versicolor_prob)
print(iris_setosa_virginica_prob)
#使用virginica验证集验证
for j in range(0,10):
iris_virginica_setosa_prob = calculateProb(iris_virginica_text[j][0],iris_setosa_train_mean[0],iris_setosa_train_var[0])\
*calculateProb(iris_virginica_text[j][1],iris_setosa_train_mean[1],iris_setosa_train_var[1])\
*calculateProb(iris_virginica_text[j][2],iris_setosa_train_mean[2],iris_setosa_train_var[2])\
*calculateProb(iris_virginica_text[j][3],iris_setosa_train_mean[3],iris_setosa_train_var[3])
iris_virginica_versicolor_prob = calculateProb(iris_virginica_text[j][0],iris_versicolor_train_mean[0],iris_versicolor_train_var[0])\
*calculateProb(iris_virginica_text[j][1],iris_versicolor_train_mean[1],iris_versicolor_train_var[1])\
*calculateProb(iris_virginica_text[j][2],iris_versicolor_train_mean[2],iris_versicolor_train_var[2])\
*calculateProb(iris_virginica_text[j][3],iris_versicolor_train_mean[3],iris_versicolor_train_var[3])
iris_virginica_virginica_prob = calculateProb(iris_virginica_text[j][0],iris_virginica_train_mean[0],iris_virginica_train_var[0])\
*calculateProb(iris_virginica_text[j][1],iris_virginica_train_mean[1],iris_virginica_train_var[1])\
*calculateProb(iris_virginica_text[j][2],iris_virginica_train_mean[2],iris_virginica_train_var[2])\
*calculateProb(iris_virginica_text[j][3],iris_virginica_train_mean[3],iris_virginica_train_var[3])
if (iris_virginica_virginica_prob>iris_virginica_setosa_prob and iris_virginica_virginica_prob>iris_virginica_versicolor_prob):
print("true")
print(countT)
countT = countT + 1
else:
print("falus")
print(countF)
countF = countF + 1
print(iris_setosa_setosa_prob)
print(iris_setosa_versicolor_prob)
print(iris_setosa_virginica_prob)
print("Accuracy为:",countT/(countT+countF),"%")
结果图片
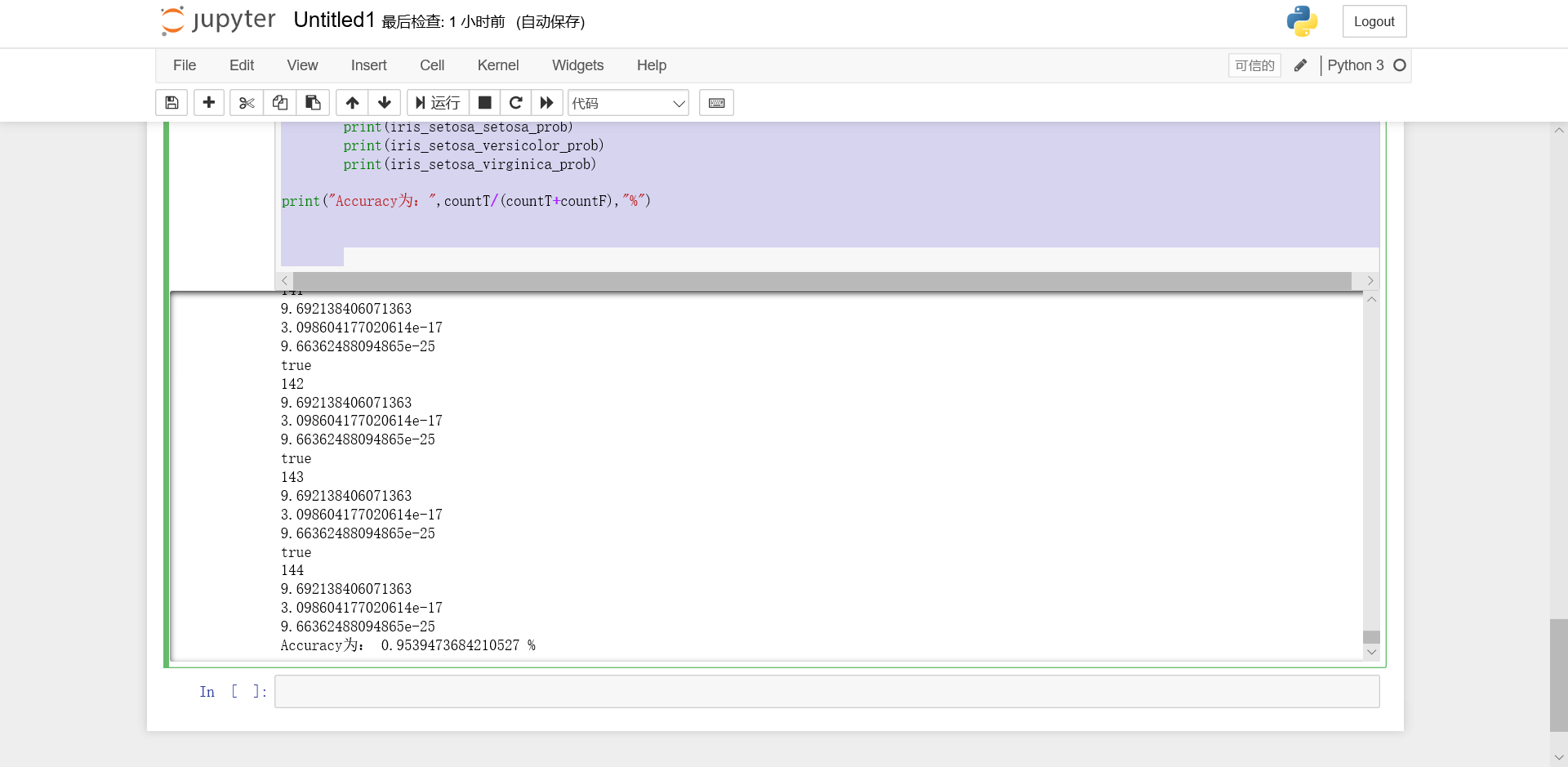
结果
Accuracy为95.39%




