洛阳师范学院ACM22级暑假前最后一次周测

玩的开心
B 一个难pizza HDU-1097
正解是:
枚举0-9每个数的次方循环
0 1 2 3 4 5 6 7 8 9 10
0: 1 0 0 0 0 0 0 0 0 0 0
1: 1 1 1 1 1 1 1 1 1 1 1
2: 1 2 4 8 6 2 4 8 6 2 4
3: 1 3 9 7 1 3 9 7 1 3 9
4: 1 4 6 4 6 4 6 4 6 4 6
5: 1 5 5 5 5 5 5 5 5 5 5
6: 1 6 6 6 6 6 6 6 6 6 6
7: 1 7 9 3 1 7 9 3 1 7 9
8: 1 8 4 2 6 8 4 2 6 8 4
9: 1 9 1 9 1 9 1 9 1 9 1
显然, 除了0次方的特殊情况, 其他都是有规律的, 要么以4个为循环(如2), 要么以2个为循环(如3)。
故直接打表+取模即可。
打表除了自己输入, 也可以直接程序输出对应的格式:
for (int i = 0; i <= a; i++)
{
cout << "{ ";
for (int j = 0; j <= 10; j++)
cout << (LL)pow(i, j) % 10 << ",}"[j == 10];
cout << "," << endl;
}
结果就是:
{ 1,0,0,0,0,0,0,0,0,0,0},
{ 1,1,1,1,1,1,1,1,1,1,1},
{ 1,2,4,8,6,2,4,8,6,2,4},
{ 1,3,9,7,1,3,9,7,1,3,9},
{ 1,4,6,4,6,4,6,4,6,4,6},
{ 1,5,5,5,5,5,5,5,5,5,5},
{ 1,6,6,6,6,6,6,6,6,6,6},
{ 1,7,9,3,1,7,9,3,1,7,9},
{ 1,8,4,2,6,8,4,2,6,8,4},
{ 1,9,1,9,1,9,1,9,1,9,1},
注意要让对应长度的第0位在首位, 如 8 对应的数组应该是 {6,8,4,2}, 长度为 4 就从 4 次方开始算。
也可以用 快速幂 硬过。
代码
#include <iostream>
#include <cmath>
using namespace std;
const int num[][4] = {
{0, 0, 0, 0},
{1, 1, 1, 1},
{6, 2, 4, 8},
{1, 3, 9, 7},
{6, 4, 6, 4},
{5, 5, 5, 5},
{6, 6, 6, 6},
{1, 7, 9, 3},
{6, 8, 4, 2},
{1, 9, 1, 9}};
const int len[] = {1, 1, 4, 4, 2, 1, 1, 4, 4, 2};
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int a, b;
while (cin >> a >> b)
{
int t = a % 10;
if (!b)
cout << 1 << endl;
else
cout << num[t][b % len[t]] << endl;
}
return 0;
}
C 塞尔达传说 王国之泪 CF-263A
求1关于终点(3,3)的曼哈顿距离。
设 1 点坐标为 \((x,y)\), 那么距离就是 \(res = |x - 3| + |y - 3|\)。
代码
#include <iostream>
#include <cmath>
using namespace std;
void solve()
{
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int x, y;
for (int i = 0; i < 5; i++)
for (int j = 0; j < 5; j++)
{
int t;
cin >> t;
if (t == 1)
x = i + 1, y = j + 1;
}
cout << abs(x - 3) + abs(y - 3) << endl;
return 0;
}
D 越狱 LibreOJ - 10196
来自信息竞赛一本通里的例题, 考察简单组合数学以及容斥原理, 当然也考了快速幂, 以及取模负数变非负数的小知识点。
有 n 个房间, 染 m 种色, 要求相邻房间同色的方案数。
易知总方案数为 \(m^n\), 且相邻房间不同色的方案数为 \(m\times (m-1) \times (m-1) \times \dots = m\times (m-1)^{n-1}\) 。
则就直接用容斥定理, 最终方案数就是 \(m^n -m\times(m-1)^{n-1}\) , 因为有取模, 故有概率会得到负数, 需要 \((x + MOD) \% MOD\) 给变成非负数。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MOD = 100003;
int qmi(LL a, LL b, int p)
{
int res = 1;
while(b)
{
if(b & 1) res = (res * a) % p;
a = (a * a) % p;
b >>= 1;
}
return res;
}
void solve() {
LL n,m;
cin >> m >> n;
cout << (qmi(m,n,MOD) - (m * qmi(m-1,n-1,MOD)) % MOD + MOD)% MOD << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
E 打桩 CF-50A
一眼看去还以为状压呢, 还好是最后让求能放多少个, 吓一跳。
做几个例子找找规律:
2x2: 2
2x3: 3, 都是 |
2x4: 4, 同上
3x3: 4, 三个 | 一个 --
3x5: 5+2, 五个 | 两个 --
5x5: 5*2+2, 十个 | 两个 --
5x10: 5*5 + 5, 二十五个 | 五个 --
猜测答案是 \(\frac{n}{2} \times m + \frac{m}{2}\)(当n是奇数时才加)。
采用贪心的策略去放, 先放竖的, 这样总共有 \(\frac{n}{2}\times m\) 个, 即 \(\frac{n}{2}\) 行, \(m\) 列, 此时对于 \(m\) 列不在乎它的奇偶, 因为每个牌只占一列。然后对于剩下的一行, 再放横的, 为 \(\frac{m}{2}\)。
有的朋友可能有个疑问, 如果是 \(n > m\) 呢? \(\frac{n\times m}{2} + \frac{m}{2}\) 肯定是把 \(n,m\) 交换之后才最大吧。这里的除法非除法, 而是特指向下取整, 因此不能把 m 塞进去。
交不交换是一样的, 各位可以自己试一试, 这里不再证明。
代码
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
if (n % 2)
cout << n / 2 * m + m / 2 << endl;
else
cout << n / 2 * m << endl;
return 0;
}
F 整数序列除法 CF-1102A
依然是枚举几个例子看看有啥规律:
1: 1 --> (1)() | 1
2: 1 2 --> (1)(2) | 1
3: 1 2 3 --> (1,2)(3) | 0
4: 1 2 3 4 --> (1,4)(2,3) | 0
5: 1 2 3 4 5 --> (1,2,4)(3,5) | 1
6: 1 2 3 4 5 6 --> (1,3,6)(2,4,5) | 1
7: 1 2 3 4 5 6 7 --> (2,5,7)(1,3,4,6) | 0
8: 1 2 3 4 5 6 7 8 --> (2,4,5,7)(1,3,6,8) | 0
9: 1 2 3 4 5 6 7 8 9 --> (1,2,4,7,9)(3,5,6,8) | 1
......
枚举策略我采用的是先奇偶分组, 然后根据相差\(d\), 挑对应差值为\(d/2\)的不同组数对交换, 找不到的话就随便挑个相差为1的换过去, 此时也大概率说明为1。
可以发现是按照 1100110011.. 这个周期来循环, 显然是一个长度为4的循环, 按照第二题的思路, 应从第4个开始, 即 0110。
代码
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int res[] = {0, 1, 1, 0};
int n;
cin >> n;
cout << res[n % 4] << endl;
return 0;
}
G 两姐妹与糖果 CF-1335A
CodeForces - 1335A 代码部队 - 1335A
给你一个数 \(n\), 在 \([1,n-1]\) 中选两个数 \(a,b\) 且满足 \(a < b\) 和 \(a + b = n\)。
二话不说做样例:
1: --> | 0
2: 1 --> | 0
3: 1 2 --> | (1,2)
4: 1 2 3 --> | (1,3)
5: 1 2 3 4 --> | (1,4), (2,3)
6: 1 2 3 4 5 --> | (1,5), (2,4)
7: 1 2 3 4 5 6 --> | (1,6), (2,5), (3,4)
...
这题可比上一题好枚举多了(
可以发现答案就是 \(\frac{n-1}{2}\)。
代码
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, T;
cin >> T;
while (T--)
{
cin >> n;
cout << (n - 1) / 2 << endl;
}
return 0;
}
H 得了一种想打APEX的病 HDU - 2602
简简单单小01背包, 直接一模板秒了。
代码
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1e3 + 10;
int v[N], w[N];
int f[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m, T;
cin >> T;
while (T--)
{
memset(f, 0, sizeof f);
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> w[i];
for (int i = 1; i <= n; i++)
cin >> v[i];
for (int i = 1; i <= n; i++)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
}
return 0;
}
I 普普通通序列 HDU - 1159
这题之前出过哦, 原题哦(
一道最长公共子序列的模板题。
定义状态: f[i][j] 从a串中选前i个, b串中选前j个的最大长度
状态转移:
若 \(a_{i}==b_i\) , 则从 \(f[i-1][j-1] + 1\) 转移。
若不等, 就从 \(f[i-1][j],f[i][j - 1]\) 转移, 挑最大的。
原题哦(
后面会附一个公共子序列模板介绍。
代码
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
const int N = 1e3 + 10;
int f[N][N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
string a, b;
while (cin >> a >> b)
{
memset(f, 0, sizeof f);
a = " " + a, b = " " + b; // 下标右移一位, 我的评价是, 不如用 char
int n = a.size() - 1, m = b.size() - 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (a[i] == b[j])
f[i][j] = max(f[i - 1][j - 1] + 1, f[i][j]);
else
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
cout << f[n][m] << endl;
}
return 0;
}
J 小奇采药 LibreOJ - 6559
一个01背包, 但没那么简单, 仔细一看数据范围, 居然背包容量能到 1e9, 但物品数只有150个, 显然这道题是用 DFS 来搜索结果。
但各位在赛后查看时可能会发现有人(指LibreOJ)用 01背包 硬过了, 只需要加上这条优化:
N = 1e5 + 10;
if (m > N)
{
m /= 10000;
for (int i = 1; i <= n; i++)
v[i] /= 10000;
}
这是因为题目中的一句话 “保证 \(m,t_i,v_i\) 在限制范围内均匀随机生成”, 类似的在 2021CCPC河南省赛也有一道题出现这个条件。往往代表着题目数据不强, 暗示你可以有一些 大胆 的想法, 而这道题, 就可以强制把大于 N 的给缩小到 N 以内来做, 当然只是体积, 价值还得是原来的。
算是奇技淫巧, 但也不得不品尝, 毕竟认真 WA 多少次也比不上一个偷跑的 AC。
当然这都是在你不会正解的情况下, 真要卡还是很简单的, 接下来介绍正解:
正常 01背包 是枚举物品再枚举体积, 而 DFS 就直接枚举所有可行方案, 每个物品有选和不选两种操作, 最坏时间复杂度为 \(O(2^{150})\), 这当然不可能过, 但也不是所有情况都成立。
DFS函数参数为 \(dfs(j,w)\) 当前方案的已用体积和总价值。
枚举前先将 \(v\) 数组从大到小排序, 这样把分支数量小的部分放前面会优化一些复杂度。
其次, 对于先选 A, 后选 B 与 先选 B, 后选 A 两种情况是等价的, 也就是说我们应该用组合的方式搜索, 而非排列的方式。
在代码中就是为 DFS函数增加一个参数 \(dfs(j,w,last)\) last表示上一步搜到了第几个物品, 接下来就从 last 继续往后搜。只看当前的物品, 递归搜索选和不选两种情况即可。
此时就已经可以过前 9 个样例了, 接下来就是更加具有启发性的剪枝优化操作。回忆一下生日蛋糕题目, 当时是用一个 \(minv\) 数组来提前把 \(v + minv > maxv\) 的情况减掉, 即当后面所有选择都选体积最小的方案, 依然会超出范围, 说明当前路线就不必选择。
同理, 这里也定义一个 \(sumW\) 数组, 如果当前 \(w+sumW_i\) 都小于之前得出的 \(res\), 那么就直接减掉。
也可以再定义一个 \(sumV\) 数组, 如果当前 \(j + sumV \le m\), 哪怕把后面所有的物品都拿上也在背包容量范围内, 那么就直接全拿了返回, 不再继续搜索。
总结下来, 这两个优化都属于 前瞻性剪枝。
对于这方面更体系的学习可以去看acwing提高课的搜索剪枝部分。
代码
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL f[N];
LL n, m;
LL res;
LL sumv[N], sumw[N];
struct Item {
LL v, w;
bool operator<(const Item &W) {
return v >= W.v;
}
} item[N];
void dfs(LL j, LL w, int last) {
if (w + sumw[last] < res)
return;
if (j + sumv[last] <= m) {
res = max(res, w + sumw[last]);
return;
}
res = max(res, w);
if (j + item[last].v <= m)
dfs(j + item[last].v, w + item[last].w, last + 1);
dfs(j, w, last + 1);
}
void solve() {
memset(f, 0, sizeof f);
res = -0x3f3f3f3f;
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> item[i].v >> item[i].w;
sort(item + 1, item + 1 + n);
for (int i = n; i >= 1; i--) {
sumv[i] = sumv[i + 1] + item[i].v;
sumw[i] = sumw[i + 1] + item[i].w;
}
dfs(0, 0, 1);
cout << res << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--)
solve();
return 0;
}
附 公共子序列
如果两个序列完全相同长度为n,一个的子序列数量是 2^n,暴力会超时,所以要用DP

状态计算如上 (这种分类为不重不漏)
01 代表缺少第i个但包含第j个
00 代表俩都缺少
从11开始分析,因为要满足包含 a[i]和b[j],所以a[i]和b[j] 一定是相等
当他们相等时,这个集合中每一个公共子序列如下:
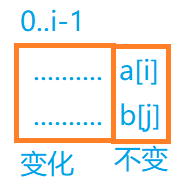
这个f[i].[j]的值便是 前面变化的公共子序列中的最大值加上1,也就是 f[i - 1][j - 1] + 1
至于00,则显然是 f[i - 1][j - 1]
01时不能用 f[i -1 ][j] 代表,因为此时表示的是 在 (0, i -1) 和 (0, j) 中选出的最长公共子序列,但不一定选到 j,有可能会变成 f[i - 1][j - 1]的结果
原则:求数量要保证不重不漏,但求最大值的时候重复可以
所以可以使用 f[i - 1]f[j],因为包含 b[j] 的情况也在里面
由此可得,f[i - 1][j - 1]会包含在 01 10 的情况中,故我们只需要求 01 10 11 的最值即可
状态转移 : f[i][j] = max(f[i - 1][j], f[i][j-1]) or max(f[i - 1][j - 1] +1) if a[i] == b[j]
优化写法:
因为只会用到 i - 1, j - 1 可以优化为 f[2][2]
只需要将上面的模板对 i % 2 即可。
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (a[i] == b[j])
f[i % 2][j % 2] = max(f[i % 2][j % 2], f[(i - 1) % 2][(j - 1) % 2] + 1);
else
f[i % 2][j % 2] = max(f[i % 2][(j - 1) % 2], f[(i - 1) % 2][j % 2]);
}
}
cout << f[n % 2][m % 2] << endl;
输出最长的序列
不能用优化写法, 保存所有路径。
我们转移是从 上, 左, 斜左上方向转移过来, 逆序思考:
斜左上转移时即说明 a[i] == b[j] 且 该点选中, 加入结果中。
左和上转移时判断 上左哪个和当前相等, 然后转移。
最后得到的就是逆序结果, 再逆序输出即可

int i = n, j = m;
while (i >= 1 && j >= 1)
{
if (a[i] == b[j])
s += b[j], i--, j--;
else if (f[i - 1][j] > f[i][j])
i--;
else
j--;
}
reverse(all(s));
cout << s << endl;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号