Team them up! - UVA 1627
#dp #线性dp #染色法划分二分图 #背包求方案 #01背包 #容斥原理 #T4
Team them up! - UVA 1627 - Virtual Judge --- 组队!- UVA 1627 - 虚拟裁判 (vjudge.net)
你的任务是将一些人分成两组,满足以下条件:
- 每个人都属于其中一个小组;
- 每个组至少有一个成员;
- 每组的每个人都认识同组的其他人;
- 各组的人数尽可能接近。
可能有多种划分方案, 你只需要输出任意一个即可, 若不存在则输出 No solution
例如,\(1\) 认识 \(2, 3, 5\);
\(2\) 认识 \(1, 3, 4, 5\);
\(3\) 认识 \(1, 2, 5\),
\(4\) 认识\(1, 2, 3\),
\(5\) 认识\(1, 2, 3, 4\)(注意 \(4\) 认识 \(1\) 但 \(1\) 不认识 \(4\) ),
则可以分两组:\(\{1,3,5\}\)和\(\{2,4\}\)。
输入
第一行输入数据组数 T。
对于每组数据:
为了简单起见,所有的人都被分配了一个从1到N的唯一的整数标识符。
第一行包含一个单一的整数N(2≤N≤100)为要分成小组的总人数
接下来是N行--按照标识符的升序,每个人一行。代表第 \(i\) 个人所认识的人。
每行包含不同数字\(A_{ij}(1≤A_{ij}≤N,A_{ij}\ne i)\)的列表,由空格分隔。
输出
对于每组数据,其输出必须遵循以下描述。两组数据的输出由一个空行分开。
如果问题的解决方案不存在,则输出'No solution'(不带引号)。
否则输出两行结果, 以单一空格分割:
第一行为第一组的人数, 然后是第一组的人员。
第二行是第二组的人数, 然后是第二组的人员。
组内人员的顺序不做要求。
样例
样例输入
2
5
3 4 5 0
1 3 5 0
2 1 4 5 0
2 3 5 0
1 2 3 4 0
5
2 3 5 0
1 4 5 3 0
1 2 5 0
1 2 3 0
4 3 2 1 0
样例输出
No solution
3 1 3 5
2 2 4
思路
题意为给一个有向关系图, 将所有点分到两个组中, 每个组内的点相互可以抵达。并输出对应的分组方案。
与其根据两两之间是否认识来划分, 不如利用容斥定理反过来思考, 定义两个点之间不认识时连一条边。那么样例就是这样一个图: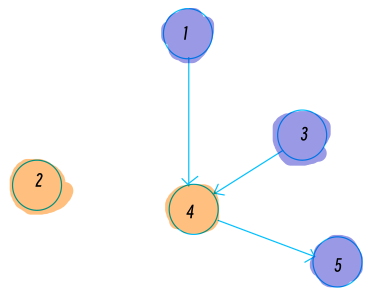
存在边的两个点无法放到一个组中, 显然对于1345这个连通块, 有两种分组方法:
- 组1:\(\{1,3,5\}\), 组2: \(\{4\}\), 对应的两组之间个数的差值 \(d = 2\)
- 组1:\(\{4\}\), 组2:\(\{1,3,5\}\), 对应的两组之间个数的差值 \(d = -2\)
也就是说, 一个连通块存在两种分组方式, 对应的差值为 \(+-d\) 。而划分时就是划分为二分图, 可以用染色法判断。
若所有的连通块都可以染色为二分图, 那么就可以得到一系列的 \(d_i\), 每个连通块有两个, 类似于分组背包, 我们找到一种选择方案, 使得最终的 \(\sum_{i=0}^{cnt}\limits{d_i}\) 最接近0。
状态定义:\(d[i][j]\) 第 \(i\) 个连通块, 当前的 \(d_{sum}\) 差值 的状态是否存在
状态转移:
采用刷表法的方式, 用 \(state_i\) 更新能到的 \(state_j\)。
初始状态 \(d[0][0 + n] = 1\)。这里因为 \(j\) 的取值范围是在 \(-n\) 到 \(n\), 下标不能为负数, 故加个偏移量。
接着枚举所有 \(d[i][j], i\subset[0,cnt), j\subset[-n,n]\), 若当前状态存在 \(d[i][j + n] == 1\) , 则更新该状态能到的新状态 \(d[i+1][j + diff[i] + n], d[i+1][j - diff[i] + n]\), 这里有两个 diff 是因为每个连通块有两种分组方式, 其对应的 \(d\) 值刚好相反。
而求差值最小的方案时, 就枚举最终结果看是否存在。先从0开始往两边找就是最小的情况。
最后输出方案时再反向遍历, 若当前结果状态可以从前一个状态 \(-diff[i]\) 转移到, 即 \(d[i][ans - diff[i] +n]\) 则说明当前结果状态是 \(+diff\) 转移过来的, 和dp时正好相反。
代码
#include <bits/stdc++.h>
using namespace std;
const int N =100 + 5;
int n, g[N][N];
int color[N]; // 二分图染色判断
int diff[N], cnt; // 记录每个连通块的队伍1和队伍2的人数差值, 连通块个数
vector<int> team[N][2]; // 第i个联通分量的c颜色的分组情况
bool dfs(int u, int c)
{
color[u] = c;
team[cnt][c - 1].push_back(u);
for(int v = 0; v < n; v++)
{
if(u != v && !(g[u][v] && g[v][u]))
{
if(color[v] > 0 && color[v] == color[u]) return false;
if(!color[v] && !dfs(v, 3 - c)) return false;
}
}
return true;
}
bool build()
{
memset(color, 0, sizeof color);
cnt = 0;
for(int i = 0; i < n; i++)
{
if(!color[i])
{
team[cnt][0].clear();
team[cnt][1].clear();
if(!dfs(i, 1)) return false;
diff[cnt] = team[cnt][0].size() - team[cnt][1].size();
cnt++;
}
}
return true;
}
int d[N][N * 2];
void print(int ans)
{
vector<int> team1, team2; // 最终的两个队伍
for(int i = cnt - 1; i >= 0; i--) // 求方案时要逆序求
{
int t; // 代表当前是哪个颜色被分到队伍1
// 因为dp时先 i + diff[i], 故逆序时也是先 - diff[i], 且因为求 diff 时默认是 team[cnt][0] - team[cnt][1]
// 即 队伍1-队伍2 的差值, 0颜色作为队伍1
if(d[i][ans - diff[i] + n]) { t = 0; ans -= diff[i]; }
// 若不存在则说明是让 1颜色作为队伍1, dp时是 - diff, 则求方案时就由 -(-diff), 即 + diff 求得
else {t = 1; ans += diff[i]; }
for(int j = 0; j < team[i][t].size(); j++)
team1.push_back(team[i][t][j]);
for(int j = 0; j < team[i][t^1].size(); j++)
team2.push_back(team[i][t^1][j]);
}
cout << team1.size();
for(int i = 0; i < team1.size(); i++) cout << " " << team1[i] + 1;
cout << endl;
cout << team2.size();
for(int i = 0; i < team2.size(); i++) cout << " " << team2[i] + 1;
cout << endl;
}
void dp()
{
memset(d, 0, sizeof d);
d[0][0 + n] = 1;
// 状态表示为: 前 i 个连通块, 总共 队伍1 - 队伍2 的人数差值为 j 的划分情况是否存在
// 因为第二维的取值范围是 -n ~ n, 故这里进行+n的偏移, 避免访问负数下标
for(int i = 0; i < cnt ;i ++)
for(int j = -n; j <= n; j++) if(d[i][j + n])
{
d[i + 1][j + diff[i] + n] = 1;
d[i + 1][j - diff[i] + n] = 1;
}
// 从小到大枚举最终的人数差, 若当前成立则当前就是最小值, 类似于二维dp的思路
for(int ans = 0; ans <= n; ans++)
{
if(d[cnt][ans + n]) { print(ans); return; }
if(d[cnt][-ans + n]) { print(-ans); return; }
}
}
void solve() {
cin >> n;
memset(g, 0, sizeof g);
for(int u = 0; u < n; u++)
{
int v;
while(cin >> v && v) g[u][v - 1] = 1;
}
// 如果无法把每个连通块划分为两组, 即二分图染色, 则说明无解
if(n == 1 || !build()) cout << "No solution" << endl;
else dp();
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while(T--)
{
solve();
if(T) cout << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号