2022ACM第二次招新题解
A - 签到题
这道超级简单的题目没有任何输入。
你只需要在一行中输出著名短句"hello world"就可以了。
代码&思路
无思路
记得完全一样就行, 别整 Hello world / helloworld / hellowrold / hello word / \"hello world\"
Ctrl+C Ctrl+v 一下就行, 循环都会写, helloword过不了怪丢人的。
#include <stdio.h>
int main()
{
printf("hello world");
return 0;
}
B - 猜猜ASCII
蒜术师知道每个字符的 ASCII 码,但是他想考考你!
输入一个除空格以外的可见字符(保证在函数scanf中可使用格式说明符%c读入),输出其 ASCII 码。
输入格式
一个可见字符。
输出格式
一个十进制整数,即该字符的 ASCII 码。
思路&代码
读个字符呗, 甚至题目都说了scanf咋写, 这不过, 就不礼貌了。
字符输出其ASCII码可以用 (int)c 强转换, 或者直接 %d, 会自动转换。
#include <stdio.h>
int main()
{
char c;
scanf("%c", &c);
printf("%d",c);
return 0;
}
C - 作为洛师的优秀学子想必你一定对除法了如指掌
今天蒜术师准备了一道带余数除法的题目,希望你能加深对它的理解并且通过这道题。
给定被除数和除数,求整数商及余数。
此题中请使用默认的整除和取余运算,无需对结果进行任何特殊处理。看看程序运行结果与数学上的定义有什么不同?
输入格式
一行,包含两个整数,依次为被除数和除数(除数非零),均在 [-106,106][−106,106] 范围内,中间用一个空格隔开。
输出格式
一行,包含两个整数,依次为整数商和余数,中间用一个空格隔开。
思路&代码
题目够长吧, 有没有被吓到(
除法是 /
取余是 %
#include <stdio.h>
int a,b;
int main()
{
scanf("%d %d", &a, &b);
printf("%d %d", a/b, a%b);
return 0;
}
D - 高富帅
某专家指出,从洛阳师范毕业的很多学生,后来都成了高富帅(especially ACM TEAM ^ ^),让我们算一算他们每个月的平均月薪是多少。
输入
输入有12行,代表12个月的薪水。
输出
输出一行,代表这一年的平均月薪。首先输出一个$,再输出每个月的平均金额。结果保留两位小数。
input
100.00
489.12
12454.12
1234.10
823.05
109.20
5.27
1542.25
839.18
83.99
1295.01
1.75
output
$1581.42
思路&代码
题目所言甚是
读入用 %f, 输出也用 %f 即可, 我见很多人用数组, 没必要哈, 定义sum为和然后除一下就行。
#include <stdio.h>
int main()
{
float sum = 0;
for(int i = 0; i < 12; i++)
{
float t = 0;
scanf("%f",&t);
sum += t;
}
printf("$%.2f\n", sum / 12.0);
return 0;
}
E - 反向反向反向反向
小蒜蒜有一个三位数,她想让聪明的你反向输出这个三位数。
输入格式
一个三位数 n\ (100\le n \le 999)n (100≤n≤999)。
输出格式
反向输出 nn,要保留前导 00。
input
100
output
001
思路&代码
水仙花低配版
设输入为 n
百位 a = n / 100
十位 b = n / 10 % 10
各位 c = n % 10
#include <stdio.h>
int main()
{
int a,b,c;
scanf("%d", &a);
b = a / 10 % 10;
c = a % 10;
a = a / 100;
printf("%d%d%d", c, b, a);
return 0;
}
F - 来点难的
输入一个长度为\(n(1 <= n <= 1000)\)的数组\(a\),元素为\(a[1]....a[n]\),之后进行\(m\)次询问,每次询问给出两个值\((l,r)(r >= l)\),求数组:\(a[l] + a[l+1] + ..... a[r]\)的值。
Input
第一行2个数,n和m,中间用空格分隔\((1 <= n, m <= 1000)\)。 之后\(n+m\)行, 第 \(1\) 至 \(n\) 行:每行一个数字\(a[i](0 <= a[i] <= 1000)\) 第 \(n + 1\) 至 \(n + m\) 行:每行2个数字\(l,r\),中间用空格分隔\((0 < l <= r <= n)\)
Output
输出共m行,每行一个数,对应\(a[l] + a[l+1] + ..... a[r]\)的值。
Data Description
对于5%的数据,\(1≤l≤r≤m≤10\),\(1≤n≤10\);
对于10%的数据,\(1≤l≤r≤m≤100\),\(1≤n≤100\);
对于100%的数据,\(1≤l≤r≤m≤1000\),\(1≤n≤1000\);
思路&代码
当我们用朴素写法时:
for(l; l <= r; l++)
sum += a[l];
显然对于 100% 的数据中, 当 m = n = 1000 且每次的 l = 1, r = 1000 时, 总时间复杂度为 \(1000\times1000 = 1e6\)
肯定不能.....诶其实是能的。
这波属于是出题失误, 不过看各位代码好像都用的前缀和。
前缀和思想就是对于数组 a[n], a[i] 表示前i个数之和, 然后就可以用 a[r] - a[l -1] 来表示区间 [l,r] 之间数的和, 这样就不需要每次计算时都遍历一下区间了, 效率更快。
#include <stdio.h>
#define N 1010
int a[N];
int main()
{
int n,m;
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
a[i] += a[i - 1];
}
while(m--)
{
int l,r;
scanf("%d %d", &l, &r);
printf("%d\n", a[r] - a[l - 1]);
}
return 0;
}
甚至朴素版跟前缀和耗时都是15ms(
G - 经典Feb
小蒜蒜最近学习了斐波那契数列。
斐波那契数列是指这样的数列:数列的第一个和第二个数都为 1,接下来每个数都等于前面 22 个数之和。
给出一个正整数 k,要求斐波那契数列中第 k 个数是多少。
输入格式
输入一行,包含一个正整数 k。\((1≤k≤46)\)
输出格式
输出一行,包含一个正整数,表示斐波那契数列中的第 k 个数。
思路&代码
依稀记得当时C语言期末考试就考了斐波那契代码, 迟早也是要学的, 等到时候你们就可以跟同学装一装了
假设数组 a[n] 来存斐波那契, 显然对于 a[i] 的值就是 a[i-1] + a[i-2]。
初始化为 a[1] = 1 即可。
这个思想在以后的动态规划算法中也有类似的体现, 各位好好体会。
// 函数写法
#include <stdio.h>
int getFeb(int k)
{
if(k == 0) return 0;
else if(k == 1) return 1;
else return getFeb(k - 1) + getFeb(k - 2);
}
int main()
{
int k;
scanf("%d", &k);
printf("%d\n", getFeb(k));
return 0;
}
但这种写法会超时:
当计算F(10)的时候,他需要先计算 F(9) 和 F(8),计算 F(8) 的时候需要计算F(7)和F(6), F(9)要算F(8)和F(7),关键在于刚才已经把F(8)算过了,所以又会去算F(8),于是又会去算F(7)和F(6)。
因此造成大量的时间浪费, 最好的方法是使用数组来进行计算, 这样只会计算一次。
也就是递推写法:
#include <stdio.h>
#define N 60
int f[N];
int getFeb(int k)
{
f[1] = 1;
for(int i = 2; i <= k; i++)
f[i] = f[i - 1] + f[i - 2];
return f[k];
}
int main()
{
int k;
scanf("%d", &k);
printf("%d\n", getFeb(k));
return 0;
}
H - Why not try this?
小明有一个数组\(a = a_1, a_2, ..., a_n\)和\(m\)次操作。每个操作如下: \(l_i, r_i, d_i, (1 ≤ l_i ≤ r_i ≤ n)\)。每一个操作意味着在\(l_i\)到\(r_i\)的区间里每个数字都加上\(d_i\)。 同时他有K次查询。每个查询有以下形式: \(x_i, y_i, (1 ≤ x_i ≤ y_i ≤ m)\)。这意味着应该对数组执行第\(x_i, x_i + 1, ..., y_i\)个操作。 现在小明的老师想知道,在执行所有查询之后,数组a会是什么。为了不让小明滚出去,请写个程序帮助他。
Input
第一行包含整数 \(n, m, k (1 ≤ n, m, k ≤ 10^5)\)。第二行包含n个整数: \(a_1, a_2, ..., a_n (0 ≤ a_i ≤ 10^5)\)——初始数组。
接下来m行包含运算,运算编号i写成3个整数:
\(l_i, r_i, d_i, (1 ≤ l_i ≤ r_i ≤ n), (0 ≤ d_i ≤ 10^5)\)。
接下来的k行包含查询,查询号i被写成两个整数: \(x_i, y_i, (1 ≤ x_i ≤ y_i ≤ m)\)。
行中的数字由单个空格分隔。
input
3 3 3
1 2 3
1 2 1
1 3 2
2 3 4
1 2
1 3
2 3
output
9 18 17
代码&思路
显然这题可不能想前缀和那样暴力了, 1e5的平方肯定超时。
所以这里需要用差分做法。
差分的思想就是先记录变化, 当需要在区间 [l,r] 加上 c 时, 在差分数组中 b[l] += c; b[r + 1] -= c;
此时, 若对差分数组做一次前缀和操作, 则 在差分数组中的 [l,r] 区间上全都是c。
那么只需要把原数组中依次加上对应差分数组中的数, 不就是区间修改么。
通过用差分来将所有变化都操作完成后, 就可以直接求出最终结果。
这里需要记录操作数组, k个询问中, 是执行 x-y 的操作。
那要直接用循环执行操作吗?
while(k--)
{
int x,y;
scanf("%d %d", &x, &y);
for(x; x <= y; x++)
//...
}
似乎也会超时, k 最大为 1e5, xy也能达到 1e5。
那么得需要两次差分, 即把每个操作的操作次数记录下来, 然后最后一起操作
#include <stdio.h>
#define N 100010
long long a[N];
int l[N], r[N], c[N];
long long A[N], b[N]; // b是A数组的差分数组, A是a数组的差分数组
int main()
{
long long n,m, k;
scanf("%lld %lld %lld", &n, &m, &k);
for(int i = 1; i <= n; i++) scanf("%lld", &a[i]);
for(int i = 1; i <= m; i++)
scanf("%d %d %d", &l[i], &r[i], &c[i]);
while(k--)
{
int x,y;
scanf("%d %d", &x, &y);
b[x]++;
b[y + 1]--;
}
for(int i = 1; i <= m; i++)
{
b[i] += b[i - 1];
int times = b[i];
A[l[i]] += (long long)times * c[i]; // 防溢出
A[r[i] + 1] -= (long long)times * c[i];
}
for(int i = 1; i <= n; i++)
{
A[i] += A[i - 1];
a[i] += A[i];
printf("%lld ", a[i]);
}
return 0;
}
I - 这道菜是您最喜欢的质数
蒜头君有一个长度为 n 的数列,第 i个数为 \(a_i\)。花椰妹最近对质数很感兴趣,所以花椰妹向蒜头君提出了 Q 个问题,对于每个问题,花椰妹想知道蒜头君的这个数列中区间 \([l,r]\) 中质数的个数。
质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数,例如 \(2,3,5,7,11,⋯\)。
输入格式
- 输入第一行一个正整数 n,表示蒜头君的数列长度。
- 第二行以空格隔开的 n 个正整数 \(a_i\),表示蒜头君的数列。
- 第三行一个正整数 Q,表示花椰妹的询问次数。
- 接下来 Q 行,第 i 行两个以空格隔开的正整数 \(l,r\),表示花椰妹的询问区间。
输出格式
输出共 Q 行,每行一个非负整数。第 i 行的数表示花椰妹第 i 次询问的结果。
数据范围
- 对于 \(20\%\)的数据,\(1\leq n,Q\leq 100, 1\leq a_i \leq 10^6\)
- 对于另外 \(30\%\) 的数据,\(1\leq n\leq 10^4, 1\leq Q \leq 10^3,1\leq a_i \leq 10^6\) ;
- 对于 \(100\%\) 的数据,\(1\leq n \leq 10^4, 1\leq Q\leq 10^6, 1\leq a_i \leq 10^6, 1\leq l\leq r \leq n\)
input
8
1 2 3 4 5 6 7 8
3
1 3
2 6
1 8
output
2
3
4
- 区间 \([1,3]\)中共有 2 个质数,分别为:\(\{2,3\}\);
- 区间 \([2,6]\)中共有 3 个质数,分别为:\(\{2,3,5\}\);
- 区间 \([1,8]\)\ 中共有 4 个质数,分别为:\(\{2,3,5,7\}\);
思路&代码
求一个区间中包含的质数的个数。
比如 1 2 3 4 5 6 7 8, 可以遍历一遍数组, 然后对每个数判断是否为素数, 若是则 sum + 1。
显然很慢, 且肯定超时, 首先可以省去素数判断, 打个表, 先把 从1 - n 的 所有素数算出来, 用 isprime[i] 来表示数 i 是不是素数, 若是则为1, 若不是则为0。
如果这么做之后会得到这样一个数组:
isprime:0 1 1 0 1 0 1 0
原数组: 1 2 3 4 5 6 7 8
然后再进行遍历 给出的 [l,r] 区间, 若 isprime[i] == 1 则 sum + 1。
既然都是1, 为啥我们不直接让 sum += isprime[i] 呢?
既然都加 isprime[i] 了, 为啥不用前缀和来实现 sum += isprime[l.r] (加上[l,r]区间的isprime[i])呢?
故总思路是先把素数打表, 然后用前缀和求区间和即可。
#include <stdio.h>
#define N 1001000
int a[N];
int isprime[N];
int main()
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
isprime[i] = 1;
if(a[i] <= 1) isprime[i] = 0;
for(int j = 2; j <= a[i] / j; j++)
if(a[i] % j == 0)
{
isprime[i] = 0;
break;
}
isprime[i] += isprime[i - 1]; // 直接求前缀和
}
int Q;
scanf("%d", &Q);
while(Q--)
{
int l,r;
scanf("%d %d", &l, &r);
printf("%d\n", isprime[r] - isprime[l - 1]);
}
return 0;
}
J - 异或矩阵

思路&代码
异或操作有三个性质:
- 满足结合律, 即
A ^ B ^ C == A ^ (B ^ C) 0 ^ A = AA ^ A = 0
显然该题不能通过遍历方法来计算, 必超时。
对于二维的矩阵运算, 我们知道有个二维前缀和, 那么是否这里也可以用上呢?
设 b[i][j] 为从 (1,1) 到 (i,j) 中所有数的异或和。
那么对于所求区间 (x1, y1) - (x2, y2), 其值就是
b[x2][y2] ^ b[x1 -1][y2] ^ b[x2][y1 - 1] ^ b[x1 - 1][y1 - 1]
为啥这么写是对的呢?
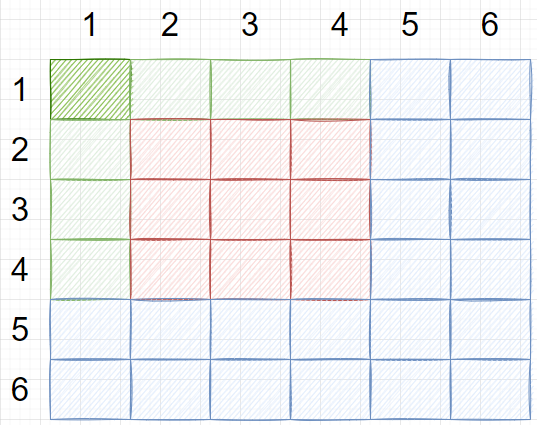
标红为 b[4][4], 若想得到 (2,2)-(4,4) 的异或和:
这里我们是多异或了b[1][4] 和 b[4][1], 根据异或的性质3, 可以通过 ^ b[1][4] ^ b[4][1] 来去掉多出来的, 但这么做之后会像二维前缀和一样多减一次 b[1][1]吗?
其实是多了, 因为在 ^b[1][4] 时, b[1][1] 就已经被减去, 然后根据性质2, 在^b[4][1]时, 又会把b[1][1] 加上。故这里仍需要 ^b[1][1] 来减去多的部分, 这样就只留下了 (2,2)-(4,4) 的异或和。
代码如下:
#include <stdio.h>
#define N 1010
int a[N][N];
int b[N][N];
int n,m;
int main()
{
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
scanf("%d", &a[i][j]);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
b[i][j] = b[i-1][j]^b[i][j-1]^b[i-1][j-1]^a[i][j];
int T = 1;
scanf("%d", &T);
while(T--)
{
int x1,y1,x2,y2;
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
printf("%d\n", b[x2][y2]^b[x1-1][y2]^b[x2][y1-1]^b[x1-1][y1-1]);
}
return 0;
}

