Hotel Atlantis Lost Cows
Hotel
题目
火山经营着一个停车场,假设的停车场有\(N\)车位(编号\(1-N\))都在一条线上,最初所有车位都没停车。经常有人来定车位,他要定连续的\(k(1 ≤ k ≤ N)\)个车位。火山要确定是否能够满足客人的要求,如果能,他要将这\(k\)个连续的车位安排在编号最小的地方停下。若不能,则客人不停在火山的停车场。在某一时间,有些车会被车主开走了。火山的停车场很大,火山想让学弟学妹写个程序帮助他。
第1行输入\(N\) 和 \(M\)。\(N\)是车位个数,M是停车和开走车操作的总次数
接下来M行,先输入操作类型(1或2)
若是1,表示有人来停车,再输入\(k\)
若是2,再输入\(l\), \(r\),表示区间\([l, l + r)\)的车被开走了。
\(N (1 ≤ N ≤ 50,000)\) \(M (1 ≤ M < 50,000)\)
当输入为1时,若火山的停车场有连续的k个车位,那么输出第一辆车停的最小的编号,否则输出0。
input
10 6
1 3
1 3
1 3
1 3
2 5 5
1 6
output
1
4
7
0
5
思路
线段树记录每个区间的最大连续未停车长度, 叶子节点就是1/0. 父节点则判断左子树的连续区间是否和右子树的连续区间连接, 如果连接则为相加后长度, 若不连接则取最大长度。
用st,ed记录当前区间的最大停车长度会导致区间内两个相同长度的区间只能用其中一个, 对后续的区间合并有很大影响。
正解是储存 lsum 从左端点向右的停车长度, rsum从右端点向左的停车长度, 至于中间的区间两端都不占则会由 msum取代(max_sum), 这个msum也可以是lsum / rsum 只要他们的长度大于中间长度(因为可以完全代替且还方便合并,中间的区间是永远无法用来合并的)。
建树:
默认全空, 则直接将 lsum = rsum = msum = len(区间长度)
更新:
因为是区间更新, 使用lazy懒更新来优化时间。(有向上更新pushup和向下更新pushdown)
设当前节点为 father, 左子树为 lson, 右子树为 rson。
- pushup:
father的lsum, 直接等于 lson的lsum
father的rsum, 直接等于 rson的rsum
father的msum, 直接等于 lson和rson的 msum 最大值
接下来考虑是否合并区间
若lson的lsum跟它的区间长度相等, 也就是说全部都可以停车, 则father的lsum = lson.lsum + rson.lsum
若rson的rsum跟它的区间长度相等, 也就是说全部都可以停车, 则father的rsum = ron.rsum + lson.rsum
至于msum, 则在(lson.msum, rson.msum, lson.rsum + rson.lsum)
最后一项是中间拼接的结果。
- pushdown:
如果lazy != -1说明需要下放标记
如果是更新0(可以停)就 lsum = rsum = msum = len(左/右子树分别为 len - len/2 / len/2)
如果是更新1(不可以停)就 lsum = rsum = msum = 0
查询:
若根节点的msum都小于k则直接输出0
若大于等于k则 优先往左边找, 左子树也大于等于k则继续找子节点。
直到找到一个节点它的左子树和右子树都小于k, 说明该区间就是要找的区间, 返回mid - 左子树的rsum + 1 即是区间最左边的点位置。
代码量很大, 但理清思路就很好写了, 注意规范码风这样不容易出现小错误。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 5e4 + 10, M = N << 2;
struct Node
{
int l, r;
int lsum, rsum, msum;
void set(int val)
{
lsum = rsum = msum = val;
}
} t[M];
int lazy[M];
void pushup(int u, int len)
{
Node &l = t[u << 1], &r = t[u << 1 | 1]; // 用引用简化代码
t[u].lsum = l.lsum, t[u].rsum = r.rsum; // 不考虑合并区间
if (l.lsum == len - (len >> 1)) // 合并区间
t[u].lsum += r.lsum;
if (r.rsum == (len >> 1))
t[u].rsum += l.rsum;
t[u].msum = max(max(l.msum, r.msum), l.rsum + r.lsum);
}
void pushdown(int u, int len)
{
if (lazy[u] != -1)
{
Node &l = t[u << 1], &r = t[u << 1 | 1];
lazy[u << 1] = lazy[u << 1 | 1] = lazy[u]; // 标记下放
if (lazy[u])
l.set(0), r.set(0);
else
l.set(len - (len >> 1)), r.set(len >> 1);
lazy[u] = -1;
}
}
void build(int l, int r, int u = 1)
{
int len = r - l + 1;
// t[u] = {l, r, len, len, len}; // POJ不支持的特性
t[u].l = l, t[u].r = r, t[u].lsum = t[u].rsum = t[u].msum = len;
if (l == r)
return;
int mid = l + r >> 1;
build(l, mid, u << 1), build(mid + 1, r, u << 1 | 1);
}
void modify(int L, int R, int val, int u = 1)
{
if (t[u].l >= L && t[u].r <= R)
{
if (val)
t[u].set(0);
else
t[u].set(t[u].r - t[u].l + 1);
lazy[u] = val;
return;
}
pushdown(u, t[u].r - t[u].l + 1);
int mid = t[u].l + t[u].r >> 1;
if (mid >= L)
modify(L, R, val, u << 1);
if (R > mid)
modify(L, R, val, u << 1 | 1);
pushup(u, t[u].r - t[u].l + 1);
}
int query(int len, int u = 1)
{
if (t[u].l == t[u].r)
return t[u].l;
pushdown(u, t[u].r - t[u].l + 1);
int mid = t[u].l + t[u].r >> 1;
if (t[u << 1].msum >= len)
return query(len, u << 1);
else if (t[u << 1].rsum + t[u << 1 | 1].lsum >= len) // 要找的最小区间
return mid - t[u << 1].rsum + 1;
else
return query(len, u << 1 | 1);
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n, m;
cin >> n >> m;
build(1, n);
memset(lazy, -1, sizeof lazy);
while (m--)
{
int op;
cin >> op;
if (op == 1)
{
cin >> op;
if (t[1].msum < op)
cout << 0 << "\n";
else
{
int res = query(op);
cout << res << "\n";
modify(res, res + op - 1, 1);
}
}
else
{
int l, r;
cin >> l >> r;
modify(l, l + r - 1, 0);
}
}
/*
for (int i = 1; i <= n + 2; i++)
cout << t[i].lsum << " " << t[i].rsum << " " << t[i].msum << endl;
*/
return 0;
}
Atlantis
题目
输入包含几个测试用例。每个测试例开始与含有可用映射的单个整数n\((1 <= N <= 100)\)的线。
接下来的n行分别描述一张地图。
每条线包含四个数字
\(x1; y1; x2; y2x1;y1;x2;y2\)
\((0<=x1<x2<=100000;0<=y1<y2<=100000)\),不一定是整数。
值\((x1; y1)\)和\((x2; y2)\)是左上角的坐标。映射区域的右下角。
输入文件由包含单个0的行终止。请勿对其进行处理。
对于每个测试用例,您的程序应输出一个部分。
每个部分的第一行必须是 Testcase #k,其中k是测试用例的编号(从1开始)。
第二个必须是Total explored area: a,其中a是总探索区(即此测试用例中所有矩形的并集面积),精确打印到小数点右边的两位数。
在每个测试用例之后输出空白行。
input
2
10 10 20 20
15 15 25 25.5
0
output
Test case #1
Total explored area: 180.00
思路
有大佬制作视频讲解
不过有些细节没讲, 看完可以参考我下面写的。
扫描线的算法如下:
图片来源:POJ1151 Atlantis(线段树,扫描线,离散化,矩形面积并)_riba2534的博客-CSDN博客
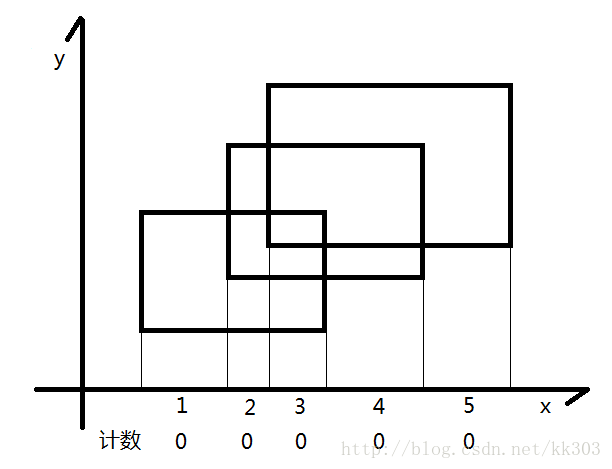
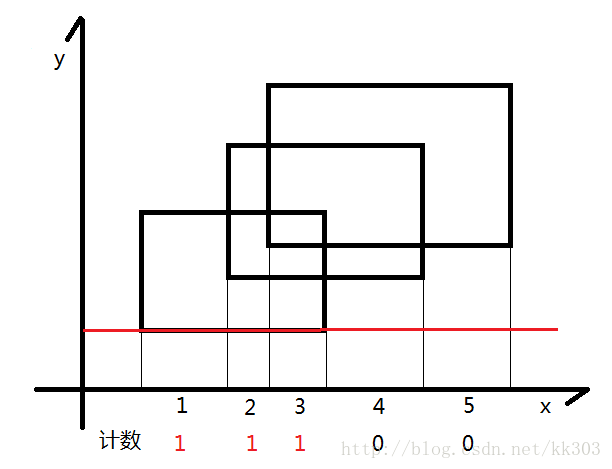
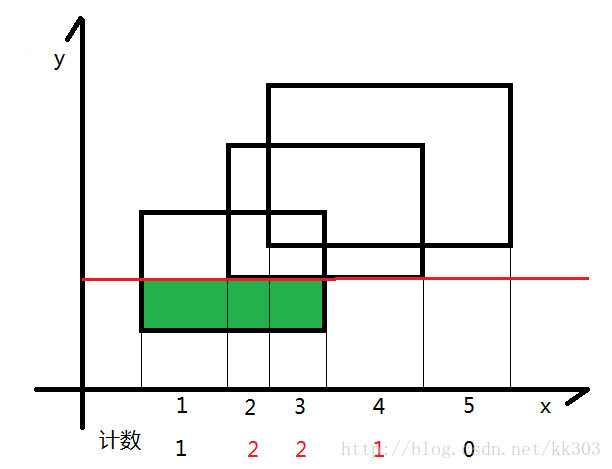
遇到新边时则扩大, 碰到之前的上边时就缩小
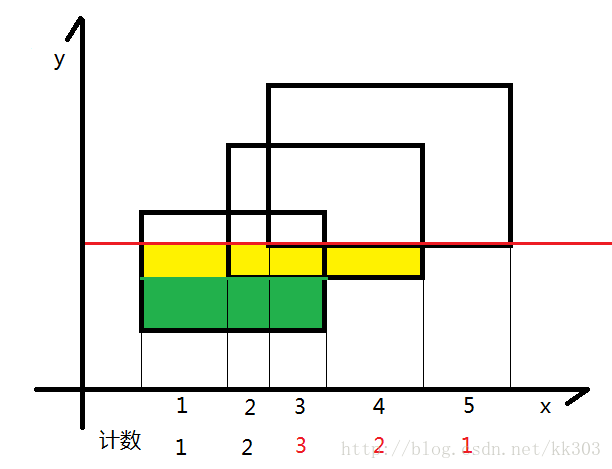
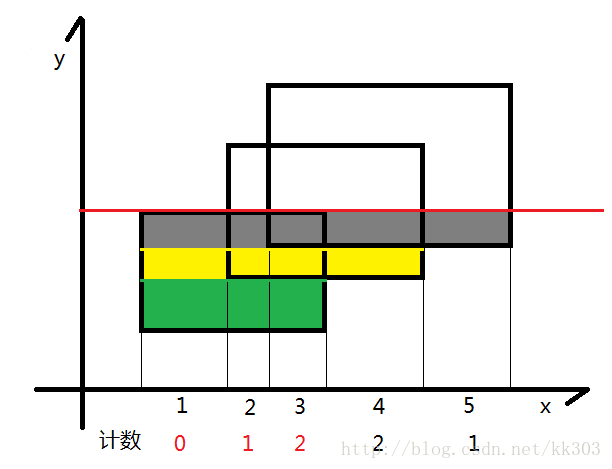
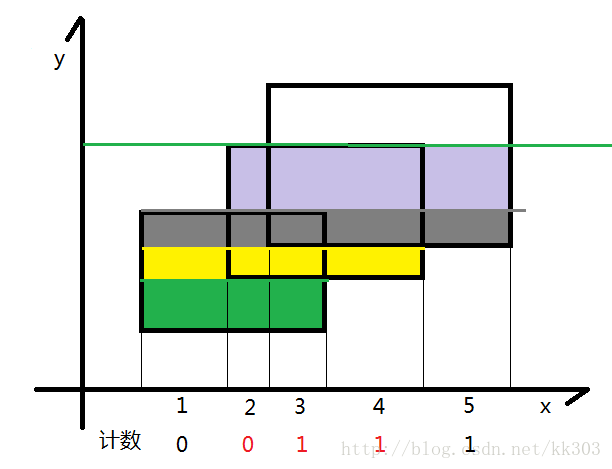
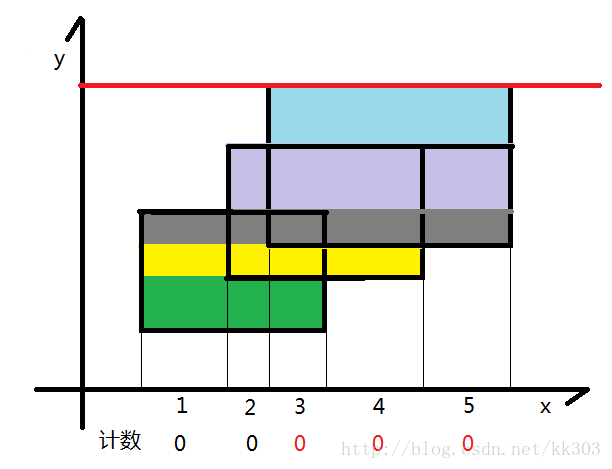
大概思路大佬那篇讲的很棒了, 我这里就配合代码讲一讲过程。
题目要求多个矩形合并起来的总面积, 以上思路中可以发现, 我们只需要存储矩形的上边和下边, 求和过程中利用线段树进行长度的变化, 从一条边扫描到另一条边时就乘上它们之间的宽度,便是这段小矩形的面积。
边的存储:
struct Seg
{
double l,r,h; // 左端点 右端点 高度
int flag; // 区分是上边还是下边
Seg(){}
Seg(double a, double b, double c, int d):l(a),r(b),h(c),flag(d){}
// 构造函数
bool operator < (const Seg &b) const
{
return h < b.h; // 根据y1 从小到大正序排序
} // 这样就从下面开始扫扫到顶端
}edge[N];
计算面积时就从低到高枚举边, res += 当前的长度 * (下一条边的高度 - 当前边的高度)
如何求当前的长度呢?
我们需要知道当前有哪些区间是正在被使用的, 可以用一个数组当做x轴, 每次查询就遍历一次数轴来统计当前长度, 这种方法首先很慢, 其次这里的数是包含小数, 不能只用下标来保存。
小数很好处理, 我们可以将所有点的x坐标进行排序, 然后利用在排序后的位置信息来遍历整个数轴。这种操作就是离散化。
既然是区间问题我们就可以使用线段树来解决:
每个节点储存当前区间的已被使用长度(len), 当前区间是否完全被使用(cnt)
需要用到的操作是区间更新和树根查询(t[1]):
区间更新正常来说是需要lazy懒标记来优化时间, 这里我们并不需要, 因为用到一个区间时并不会去关心它的子区间, 如果一个区间被完全使用, 那么它就可以被当做一个叶子区间(最小区间),不需要再往下划分。
所以只需要一个 pushup 操作来更新父节点:
void pushup(int l, int r, int u)
{
if(t[u].cnt) // 如果当前区间被完全使用
t[u].len = x[r + 1] - x[l]; // 加上当前区间的长度 右端点-左端点
else if(l == r) // 若左右端点相同则长度为0
t[u].len = 0;
else // 未被完全使用的话就是子区间被使用的长度之和
t[u].len = t[u << 1].len + t[u << 1 | 1].len;
}
为什么用 x[r + 1] 而不是 x[r]?
线段树存的并不是当前 [l,r] 的长度, 而是 [l, r + 1] 的长度, 避免出现 [3,3] 这种即是点又是线段的情况出现, 保证每个节点都存的是一条线段, 也方便判断当前区间是否为点(l == r)。
需要构建一个树嘛?不需要, 默认值就是0,我们只用实现update方法即可:
void update(int L,int R, int l, int r, int u, int val) // LR是目标区间,lr是线段树区间
{
if(L <= l && R >= r) // 若当前节点在目标区间内
{
t[u].cnt += val; // val为1则加上该边, 为-1则减去该边
pushup(l,r,u); // 直接更新, 可以不用这个, 只写 t[u].len = x[r + 1] - x[l] 不过效果一样
return;
}
int mid = l + r >> 1;
if(L <= mid)
update(L,R,l,mid,u << 1, val);
if(R > mid)
update(L,R,mid+1,r,u<< 1 | 1, val);
pushup(u);
}
main函数里面就看下面代码的注释吧。
这题是相当难的一道线段树, 不仅仅是用到了扫描线扩展知识, 重要的是把每个节点的值都看成线段和每个节点都有含义这两个思想, 对于深刻理解线段树很有帮助(编的)
不过写出来之后确实感觉很棒, 各位加油!
参考博客:
【hdu1542】线段树求矩形面积并 - 拦路雨偏似雪花 - 博客园 (cnblogs.com)
POJ1151 Atlantis(线段树,扫描线,离散化,矩形面积并)_riba2534的博客-CSDN博客
代码
#include <iostream>
#include <iomanip>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 220;
struct Seg
{
double l, r, h;
int flag;
Seg() {}
Seg(double l, double r, double h, int flag) : l(l), r(r), h(h), flag(flag) {}
bool operator<(const Seg &b) const
{
return h < b.h;
}
} edge[N];
struct Node
{
int cnt; // 该区间是否被完全使用上
double len;
} t[N << 2];
double x[N]; // 用来离散化储存坐标x
void pushup(int l, int r, int u)
{
if (t[u].cnt)
t[u].len = x[r + 1] - x[l];
else if (l == r) // 该区间未全被使用
t[u].len = 0;
else // 当前区间没占满, 为两个子节点区间长度之和
t[u].len = t[u << 1].len + t[u << 1 | 1].len;
}
void update(int L, int R, int l, int r, int u, int val)
{
if (L <= l && R >= r)
{
t[u].cnt += val;
pushup(l, r, u);
return;
}
int mid = l + r >> 1;
if (L <= mid)
update(L, R, l, mid, u << 1, val);
if (R > mid)
update(L, R, mid + 1, r, u << 1 | 1, val);
pushup(l, r, u);
}
int main()
{
cin.tie(0)->sync_with_stdio(false); // 快读
cout << fixed << setprecision(2); // 保留两位小数 iomanip
int n, kase = 0;
while (cin >> n && n)
{
memset(t, 0, sizeof t);
int cnt = 0; // 用于存放数据的下标
for (int i = 0; i < n; i++)
{
double a, b, c, d;
cin >> a >> b >> c >> d;
x[cnt] = a, edge[cnt++] = Seg(a, c, b, 1); // 上边
x[cnt] = c, edge[cnt++] = Seg(a, c, d, -1); // 下边
}
sort(x, x + cnt);
/*
for (int i = 0; i < cnt; i++)
cout << x[i] << " ";
cout << endl;
*/
sort(edge, edge + cnt);
int m = unique(x, x + cnt) - x; // 不重复部分的尾部
double res = 0;
for (int i = 0; i < cnt; i++)
{
int l = lower_bound(x, x + m, edge[i].l) - x; // 二分查找
int r = lower_bound(x, x + m, edge[i].r) - x - 1;
//cout << i << ": " << l << " " << r << endl;
update(l, r, 0, m, 1, edge[i].flag); // 加边 或者 减边
res += t[1].len * (edge[i + 1].h - edge[i].h); // 长 * (宽)
//cout << "len : " << t[1].len << endl;
}
cout << "Test case #" << ++kase << "\nTotal explored area: " << res << "\n\n";
}
}
Lost Cows
题目
有n只小动物,每只都有一个独特的编号,分别从1到n。现在他们从左到右依次排在一条直线上,顺序是乱的。
现在,我们只知道每个位置前面有几个比他小的数。请你根据给出的信息计算出每个位置上的数是多少。
n<=80000。
输入第一行是一个正整数n,表示小动物的数量。
接下来有n-1个数,第i个数表示在第i+1个位置以前有多少个比第i+1个位置上的数小的数。
输出n行,每行一个整数,表示对应位置小动物的编号。
input
5
1
2
1
0
output
2
4
5
3
1
思路
画个图看看:

整体上来看没什么思路, 我们从后往前单独看最后一个数, 比它小的在前面有4个, 又知总共有6个数, 显然这个数就应该为5。
同理到倒数第二个数时, 前面4个数中比它小的只有一个, 故肯定为2.
枚举到导数第四个数时, 当前已经确定的位置有 [? 2 ? 4 5 ?], 且前面未确定的数中比当前数小的有2个, 说明该数应该在最后一位,为6。
因此可以推断出, a[i] + 1 就是 a[i] 在未确定数中的位置。
朴素方法可以声明一个 vis[] 数组记录每个数是否确定, 然后从1到n枚举直到未确定的数数量等于 a[i] + 1, 此时的下标就是该位置上的数。
优化方法:
同样是vis数组我们求前缀和之后可以通过二分快速找到 a[i] + 1。
因为每次确定一个数之后, 未确定数的数量就会变化, 不能用前缀和, 这里可以用树状数组/线段树来快速处理。
总共用到的只有区间求和和单点修改。
注意二分查询时的边界条件, 如果是这样会死循环:(我也不知道为啥)
while(l < r)
{
int mid = l + r + 1 >> 1;
if(query(1,mid,1,n) <= a[i] + 1)
l = mid;
else
r = mid - 1;
}
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 8e5 + 10, M = N << 2;
int t[M];
int a[N], ans[N];
void build(int l, int r, int u = 1)
{
if (l == r)
{
t[u] = 1;
return;
}
int mid = l + r >> 1;
build(l, mid, u << 1), build(mid + 1, r, u << 1 | 1);
t[u] = t[u << 1] + t[u << 1 | 1];
}
int query(int L, int R, int l, int r, int u = 1)
{
if (L <= l && R >= r)
{
return t[u];
}
int mid = l + r >> 1;
int res = 0;
if (L <= mid)
res += query(L, R, l, mid, u << 1);
if (R > mid)
res += query(L, R, mid + 1, r, u << 1 | 1);
return res;
}
void modify(int idx, int l, int r, int u = 1)
{
if (l == r)
{
t[u] = 0;
return;
}
int mid = l + r >> 1;
if (mid >= idx)
modify(idx, l, mid, u << 1);
else
modify(idx, mid + 1, r, u << 1 | 1);
t[u] = t[u << 1] + t[u << 1 | 1];
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n;
cin >> n;
for (int i = 2; i <= n; i++)
cin >> a[i];
build(1, n);
for (int i = n; i > 0; i--)
{
int l = 1, r = n;
while (l < r) // 二分找所有前缀和位置中等于 a[i] + 1的位置
{
int mid = (l + r) >> 1;
if (query(1, mid, 1, n) >= a[i] + 1)
r = mid;
else
l = mid + 1;
}
ans[i] = r;
modify(r, 1, n); // 将该数标记为已确定
}
for (int i = 1; i <= n; i++)
cout << ans[i] << "\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号