S-Nim | Brave Game | Good Luck in CET-4 Everybody!
Brave Game
题目
十年前读大学的时候,中国每年都要从国外引进一些电影大片,其中有一部电影就叫《勇敢者的游戏》(英文名称:Zathura),一直到现在,我依然对于电影中的部分电脑特技印象深刻。
今天,大家选择上机考试,就是一种勇敢(brave)的选择;这个短学期,我们讲的是博弈(game)专题;所以,大家现在玩的也是“勇敢者的游戏”,这也是我命名这个题目的原因。
当然,除了“勇敢”,我还希望看到“诚信”,无论考试成绩如何,希望看到的都是一个真实的结果,我也相信大家一定能做到的~
各位勇敢者要玩的第一个游戏是什么呢?很简单,它是这样定义的:
1、 本游戏是一个二人游戏;
2、 有一堆石子一共有\(n\)个;
3、 两人轮流进行;
4、 每走一步可以取走\(1…m\)个石子;
5、 最先取光石子的一方为胜;
如果游戏的双方使用的都是最优策略,请输出哪个人能赢。
input
2
23 2
4 3
output
first
second
思路
把 \(n\) 个石子分为 \(k\) 堆, 每堆 \(m+1\) 个。
若刚好 \(k\) 堆, 每堆都是 \(m+1\) 个, 则先手必输。
证明:
若只有一堆, 那么先手无论是取1, 还是取m, 最后都会剩下一部分, 而这一部分能被后手全部取完。
若 \(k\) 堆, 同样如此, 先手取任意一堆中一部分, 这堆中剩下部分都能被直接取完, 那么到最后还是剩一堆 \(m+1\) 且仍先手取。
若 \(k\) 堆, 第 \(k\) 堆不足 \(m+1\) 个, 则先手必赢。
证明:
由上个结论可得, 若每堆数量都是 \(m+1\) 则先手必输, 这里多出一堆小于\(m+1\)的, 当先手把这一小堆拿走后, 剩下的就是先手必输局面。
代码
#include <iostream>
using namespace std;
int main()
{
int T;
cin >> T;
while(T--)
{
int n,m;
cin >> n >> m;
if(n % (m + 1)) cout << "first\n";
else cout << "second\n";
}
return 0;
}
Good Luck in CET-4 Everybody!
题目
大学英语四级考试就要来临了,你是不是在紧张的复习?也许紧张得连短学期的ACM都没工夫练习了,反正我知道的Kiki和Cici都是如此。当然,作为在考场浸润了十几载的当代大学生,Kiki和Cici更懂得考前的放松,所谓“张弛有道”就是这个意思。这不,Kiki和Cici在每天晚上休息之前都要玩一会儿扑克牌以放松神经。
“升级”?“双扣”?“红五”?还是“斗地主”?
当然都不是!那多俗啊~
作为计算机学院的学生,Kiki和Cici打牌的时候可没忘记专业,她们打牌的规则是这样的:
1、 总共n张牌;
2、 双方轮流抓牌;
3、 每人每次抓牌的个数只能是2的幂次(即:1,2,4,8,16…)
4、 抓完牌,胜负结果也出来了:最后抓完牌的人为胜者;
假设Kiki和Cici都是足够聪明(其实不用假设,哪有不聪明的学生~),并且每次都是Kiki先抓牌,请问谁能赢呢?
当然,打牌无论谁赢都问题不大,重要的是马上到来的CET-4能有好的状态。
input
1
3
output
Kiki
Cici
思路
做完上一题之后, 可以总结出一个方向, 若可以把总数分成多个先手必输的局面即必输态, 且无论何时都能让后手所遇到的局面为必输态, 那么就是先手必胜态,
上一题中就是分为 \(m+1\) 堆石子, 这一堆中谁先手必输。
这题取法不相同, 可以取所有的偶数。
显然若\(n\)为偶数或\(1\), 先手可直接取完, 为必胜态,
若\(n\)为奇数, 则将其分为 \(k\) 堆, 每堆 \(3\) 张牌, 对于每一堆, 先手只能取\(2\), 故为必输态。
此时和上一题已经是一样的思路了:
若刚好每堆都是 \(3\) 那就是先手必输, 若有一堆没分满\(3\), 则为先手必胜态。
代码
#include <iostream>
using namespace std;
int main()
{
int n;
while(cin >> n)
{
if(n % 3) cout << "Kiki\n";
else cout << "Cici\n";
}
return 0;
}
S-Nim
S-Nim
两个人玩游戏,规则是有 n 堆石子,分别有 \(a_1,a_2,…,a_n\)颗石头,每次从一堆石子中取一些石子,但是可取的石子数是规定了的,必须是 \(s_1,s_2,…,s_k\) 中的一个,谁无法操作就输。
input
2 2 5
3
2 5 12
3 2 4 7
4 2 3 7 12
5 1 2 3 4 5
3
2 5 12
3 2 4 7
4 2 3 7 12
0
output
LWW
WWL
思路
是否可以用之前的思路来写呢?把n堆合并成一堆, 然后找必胜态。
显然不行, 三个 \(1\) 石子 的堆并不能拿 \(3\) 个。
引入SG函数:
Mex运算:
设S表示一个非负整数集合.定义\(mex(S)\)为求出不属于集合\(S\)的最小非负整数运算,即:
\(mes(S)=min{x}\);
例如:\(S={0,1,2,4}\),那么\(mes(S)=3\);
SG函数:
在有向图游戏中,对于每个节点\(x\),设从\(x\)出发共有\(k\)条有向边,分别到达节点\(y1,y2,····yk\),定义\(SG(x)\)的后记节点\(y1,y2,····\)
\(yk\)的\(SG\)函数值构成的集合在执行\(mex\)运算的结果,即:
\(SG(x)=mex({SG(y1),SG(y2)····SG(yk)})\)
特别地,整个有向图游戏\(G\)的\(SG\)函数值被定义为有向图游戏起点\(s\)的\(SG\)函数值,即 \(SG(G)=SG(s)\).
有向图游戏的和
设\(G_1,G_2,····,G_m\)是\(m\)个有向图游戏.定义有向图游戏\(G\),他的行动规则是任选某个有向图游戏\(G_i\),并在\(G_i\)上行动一步.\(G\)被称为有向图游戏\(G_1,G_2,·····,G_m\)的和.
有向图游戏的和的\(SG\)函数值等于它包含的各个子游戏\(SG\)函数的异或和,即:
\(SG(G)=SG(G_{1}) \wedge SG(G_2) \wedge··· \wedge SG(G_m)\)
先来看看简单的样例:
假设取石子的集合 \({2,5}\) , 仅有一堆石子, 石子数为 \(10\):
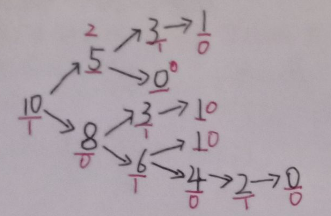
求出整个图的SG函数值(红色即是该节点的SG值)
可以发现:当SG值为0时, 从该点先手一定会输。
再根据有向图游戏的和性质, 若所有堆石子数异或后的结果为0, 则先手必输。
计算所有SG函数时使用记忆化搜索, 也算枚举了所有选择的可能, 相当暴力的做法, 复杂度为指数级别。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <unordered_set>
using namespace std;
//------- Coding Area ---------//
const int N = 1e2 + 10, M = 1e4 + 10; //f数组设大一点
int n, m, k;
int s[N], f[M];
int SG(int x)
{
if (f[x] != -1)
return f[x];
bool st[110];
memset(st, false, sizeof st);
for (int i = 0; i < k; i++)
if(x >= s[i])
st[SG(x-s[i])] = 1;
for (int i = 0;; i++)
if (!st[i])
return f[x] = i;
}
int main()
{
while (cin >> k && k)
{
memset(s, 0, sizeof s);
memset(f, -1, sizeof f);
for (int i = 0; i < k; i++)
scanf("%d", &s[i]);
//sort(s, s + k); 很多博客这里会加sort, 其实可以不加, 具体看下文
scanf("%d", &m);
while(m--)
{
scanf("%d", &n);
int res = 0;
while(n--)
{
int x;
scanf("%d", &x);
res ^= SG(x);
}
if (res)
printf("W");
else
printf("L");
}
printf("\n");
}
return 0;
}
有关是否排序
S-Nim(hdu1536+SG函数)_寻找星空的孩子的博客-CSDN博客

这篇博客说一定要排序, 但经过测试后证明不需要排序也可以。
用 time.h 和 algorihtm 的 random_suffle 函数将数组乱序, 效果如下:

应用到题目中然后提交可以AC:
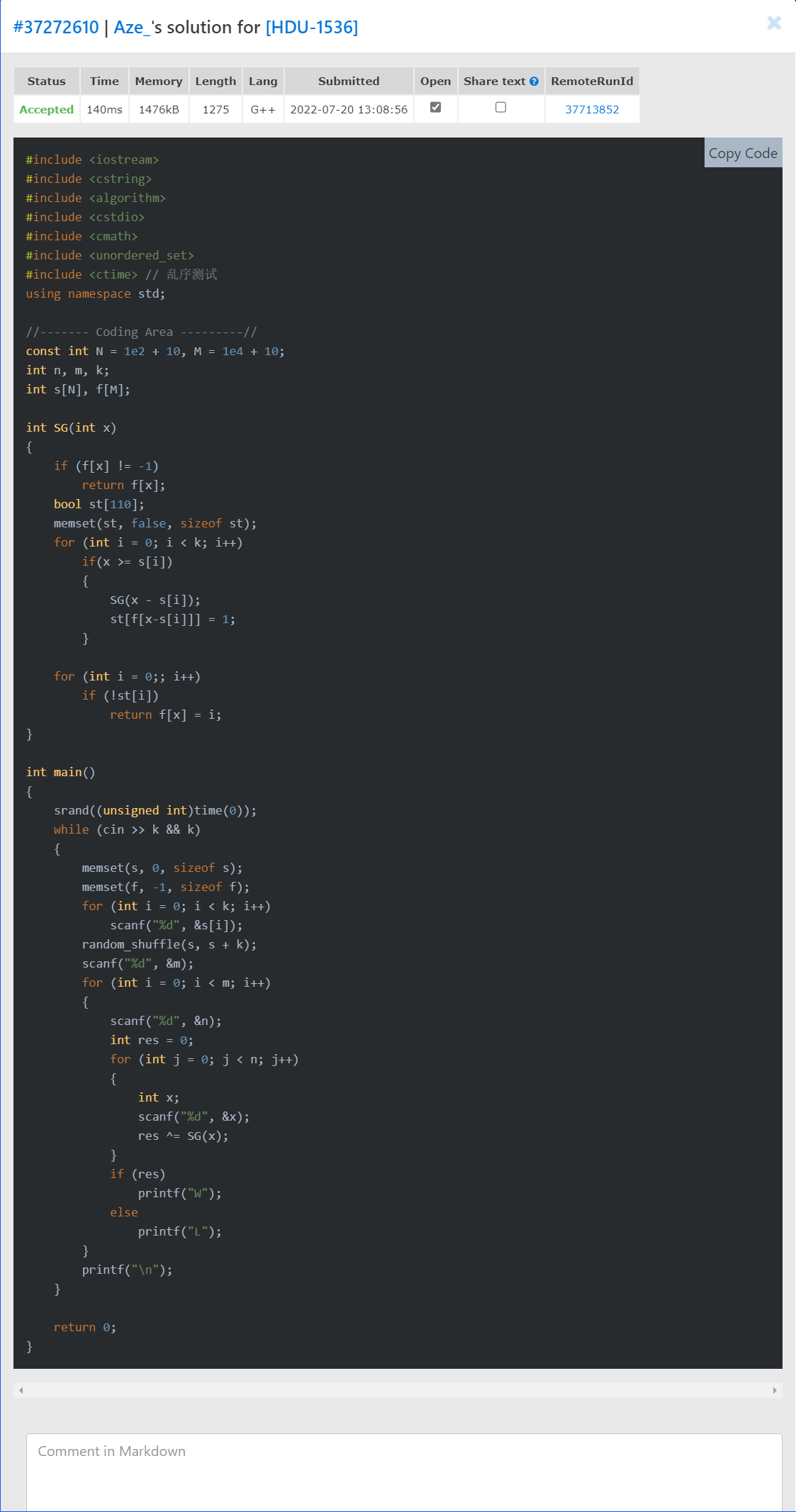
在时间上有sort和无sort的区别:

差别不大, 毕竟SG函数本身就是 \(n^2\) 的算法, 多个 \(n\log n\) 没差多少
感谢syf学长的指导(


 浙公网安备 33010602011771号
浙公网安备 33010602011771号