Corn Fields 单词接龙 Bugs Integrated
Corn Fields
农场主John新买新牧场,这块牧场被划分成M行N列(1 ≤ M ≤ 12; 1 ≤ N ≤ 12),每一格都是一块正方形的土地。John打算在牧场上的某几格里种上美味的草,供他的奶牛们享用。
遗憾的是,有些土地相当贫瘠,不能用来种草。并且,奶牛们喜欢独占一块草地的感觉,于是John不会选择两块相邻的土地,也就是说,没有哪两块草地有公共边。
John想知道,如果不考虑草地的总块数,那么,一共有多少种种植方案可供他选择?(当然,把新牧场完全荒废也是一种方案)
Input
第一行:两个整数M和N,用空格隔开。
第2到第M+1行:每行包含N个用空格隔开的整数,描述了每块土地的状态。第i+1行描述了第i行的土地,所有整数均为0或1,是1的话,表示这块土地足够肥沃,0则表示这块土地不适合种草。
Output
一个整数,即牧场分配总方案数除以100,000,000的余数。
Sample Input
2 3
1 1 1
0 1 0
Sample Output
9
思路
蒙德里安那道题的一种应用, 依然是用二进制来表示该列上哪个位置种草。
总思路就是枚举所有可行状态, 然后计算转移, 最后得出结果方案数。
直接迁移思考路径, 先考虑怎样的一列是成立的:
题目要求任意两块草坪不能相邻, 相比于蒙德里安要简单一些, 只需要用个计数来判断是否存在相邻草坪即可
for(int i = 0; i < 1 << n; i++)
{
bool cnt = false, flag = false;
for(int j = 0; j < n; j++)
{
if(i >> j & 1) // 这一位是1, 种草坪
{
if(cnt) // 如果相邻一位也是1
{
flag = true;
break;
}
else cnt = true;
}
else cnt = false;
}
if(!flag) ...; // 如果成立再进行下一步操作
}
接着考虑某一个状态可以从哪个状态中转移过去:
设 第i列 当前状态为 j, i - 1列 状态为 k, 初始状态可以转移
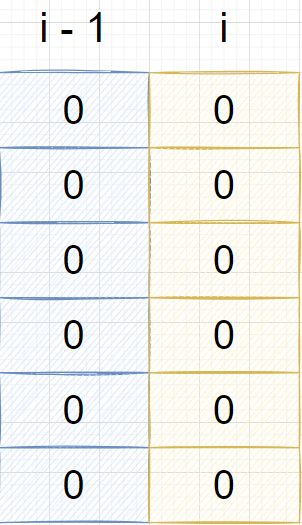
当出现相邻1时, 不能转移(不成立):
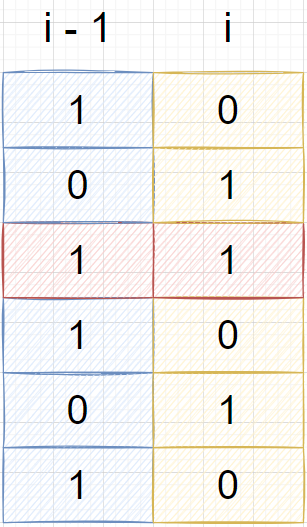
故需要满足 k & j == 0。
题目上还有一个条件, 有的地方是不能种草坪的, 所以在判断某列是否成立时, 需要加上判定:
for(int k = 1; k <= n; k++)
for(int i = 0; i < 1 << m; i++)
{
bool cnt = false, flag = false;
for(int j = 0; j < m; j++)
{
if(i >> j & 1) // 这一位是1, 种草坪
{// k 表示某一列, 这里无论j是否能将题目中数组对应上二进制的位置, 对结果没有影响, 因为需要在意的只是相对位置
if(cnt || g[k][j] == 0) // 如果相邻一位也是1
{
flag = true;
break;
}
else cnt = true;
}
else cnt = false;
}
if(!flag) ...; // 如果成立再进行下一步操作
}
最后的结果怎么求:
遍历最后一列的所有状态, 将其加起来即可。
for(int i = 0; i < 1 <<m; i++)
{
if(check(i))
res += f[n][i];
}
对于当前列状态是否有效还有一种更巧判断方法:
判断是否存在相邻1可以 (x&(x >> 1)) && (x&(x <<1)) 若左/右移后再&结果不为0 则说明存在相邻, 整个表达式返回0时才说明状态存在。
判断是土地是否肥沃可以先将输入处理成同样的状态表示 map[i] , 若状态 x 可以存在, 说明 x & map[i] == x。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
//------- Coding Area ---------//
const int N = 15,M = 1 << N, MOD = 100000000; // M是状态
int n, m;
int g[N][N], f[N][M], map[N];
long long res;
bool check(int k,int x) // 第k列的状态x
{
bool flag1 = (x & (x >> 1)) && (x & (x << 1));
bool flag2 = (x & map[k]) != x;
return !(flag1 || flag2);
}
int main()
{
cin >> m >> n;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
cin >> g[j][i];
// 处理输入
for (int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
map[i] = (map[i] << 1) + g[i][j];
}
// 起始状态计算
for (int i = 0; i < 1 << m; i++)
if (check(0,i)) f[0][i] = 1;
// 开始DP
for (int i = 1; i < n; i++)
{
for (int j = 0; j < 1 << m; j++)
{
for (int k = 0; k < 1 << m; k++)
{
if ((j & k) == 0 && check(i, j) && check(i - 1, k))
f[i][j] = (f[i][j] + f[i - 1][k]) % MOD;
}
}
}
// 找出答案
for (int i = 0; i < 1 << m; i++)
{
if (check(n - 1, i)) res = (res + f[n - 1][i]) % MOD;
}
cout << res << endl;
return 0;
}
单词接龙
单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙”中出现两次),在两个单词相连时,其重合部分合为一部分,例如 beast和 astonish,如果接成一条龙则变为 beastonish ,另外相邻的两部分不能存在包含关系,例如 at 和 atide 间不能相连。
输入格式
输入的第一行为一个单独的整数 n (n \le 20)n(n≤20) 表示单词数,以下 nn 行每行有一个单词,输入的最后一行为一个单个字符,表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。
输出格式
只需输出以此字母开头的最长的“龙”的长度。
样例说明
连成的“龙”为 atoucheatactactouchoose
Sample 1
Input
5
at
touch
cheat
choose
tact
a
Output
23
思路
参考:题解 P1019 【单词接龙】 - FeTieTer - 洛谷博客 (luogu.com.cn)
!!该解法不是标准解法, 因为题目数据太水所以可行!!
因为每个单词都可以选两次, 但状压DP只能选一次, 所以需要将单词复制一份
复制一份之后 n *= 2, 会导致状态大小超出 int 2^32 范围 (1 << 32), 从而 MLE(内存超限)
不过该题经测试 n <= 8, 所以 状态数 为 1 << 16 就能过。
---正文----
状态压缩就是将所有能选的情况化为二进制01来表示, 然后计算状态转移, 最后得出结果。
这里的状态就是单词选择情况。
上一题是用 第i - 1列 转移到 第i列, 这里则是从 没选择第i个单词的情况 到 选择第i个单词的情况。
状态表示: f[i][j] i是二进制表示所有单词的选择情况, j表示以第j个单词结尾
状态属性: max
状态计算: f[i][j] = max(f[i][j], f[q][k] + len[k][j]);
q表示没有选上第j个单词的状态, k表示q状态的结尾单词
len[k][j] 就是j接到k单词后面所增加的长度
最后的结果需要在计算过程中找最大值:
ans = max(ans, f[i][j]);
如何得到len数组呢:
两层循环枚举所有单词, 对于 单词a 和 单词b:
当 a b 互不包含, 且 a单词末尾存在与b单词开头相同的部分时, b可以接在a后面
判断a b是否互不包含:
string a, b;
if((strstr(a.c_str(), b.c_str())
|| strstr(b.c_str(). a.c_str()))
&& a.size() != b.size()) // a==b 时不算包含
return 不能接;
判断a b是否可以接上且接上后增加多少长度:
for(int k = a.size() - 1; k >= 0; k--)
{
if(a[k] == b[0])// 当找到a中一个与b起始字母相同的便开始判断
{
int j = 0, i = k;
for(i,j; i < a.size(), j < b.size(); i++,j++)
if(a[i] != b[j]) break; // 这个选点不对
if(i == a.size()) return b.size() - j; // b.size() - j 即是增加长度
}
}
return -1;
加起来就是怎样判断b是否能接到a:
int check(string a, string b)
{
if((strstr(a.c_str(), b.c_str()) || strstr(b.c_str(), a.c_str()) && a.size() != b.size())) return -1;
for (int k = a.size() - 1; k >= 0; k++)
{
if (a[k] == b[0])
{
int i = k, j = 0; // 双指针算法
for (; i < a.size(), j < b.size(); i++, j++)
if (a[i] != b[j]) break;
if (i == a.size() - 1) return b.size() - j;
}
}
return -1;
}
计算len:
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i == j) continue;
else {
int t = check(word[i], word[j]);
if (t == 0) t = -1; // 为了省时间把不增加的也给表示成无法接上
lens[i][j] = t;
}
得到len数组之后, 就可以开始DP啦:
初始条件处理
char tmp; cin >>tmp;
for (int i = 0; i < n; i++)
{
if (word[i][0] == tmp)
{
f[1 << i][i] = word[i].size(); // 1 << i 是只选中第i个单词的状态
ans = max(f[1 << i][i], ans);
}
}
代码
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
//------- Coding Area ---------//
const int N = 1010, M = 1 << 16; // M是状态
int n, m;
string word[N];
int f[M][17], lens[N][N];
int check(string a, string b)
{
if((strstr(a.c_str(), b.c_str()) || strstr(b.c_str(), a.c_str())) && a.size() != b.size()) return -1;
for (int k = a.size() - 1; k >= 0; k--)
{
if (a[k] == b[0])
{
int i = k, j = 0; // 双指针算法
for (; i < a.size() && j < b.size(); i++, j++)
if (a[i] != b[j]) break;
if (i == a.size()) return b.size() - j;
}
}
return -1;
}
int main()
{
memset(f, -1, sizeof f);
cin >> n;
for (int i = 0; i < n; i++) cin >> word[i];
for (int i = n; i < n * 2; i++) word[i] = word[i - n]; // 复制一份
n *= 2;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i == j) continue;
else {
int t = check(word[i], word[j]);
if (t == 0) t = -1;
lens[i][j] = t;
}
getchar(); // 吃换行
char tmp;
cin >> tmp;
int ans = 0;
// dp初始状态处理
for (int i = 0; i < n; i++)
{
if (word[i][0] == tmp)
{
f[1 << i][i] = word[i].size();
ans = max(f[1 << i][i], ans);
}
}
// 开始dp
for (int i = 0; i < (1 << n); i++)
{
for (int j = 0; j < n; j++) // 准备选第j个单词
{
if ((i >> j) & 1) continue; // 若已经选上则返回
for (int k = 0; k < n; k++)
{
if (((i >> k) & 1) && lens[k][j] != -1 && f[i][k] != -1)
{// 若当前状态k已被选上 且 j能接到k后面 且 转移前状态已被计算
f[i | (1 << j)][j] = max(f[i | (1 << j)][j], f[i][k] + lens[k][j]);
ans = max(ans, f[i | (1 << j)][j]);
}
}
}
}
cout << ans << endl;
return 0;
}
Bugs Integrated, Inc.
https://www.cnblogs.com/autoint/p/10794147.html
看这个大佬的吧, 比我的清楚多了(〃'▽'〃)
问题收集
有啥没搞懂的私聊问我, 之后会贴在这方便有同样问题的朋友。(虽然我也没自信说会)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号