[算法简结]递归分治(二):合并排序
在上一篇中,我们知道了递归分治的一些理论知识以及一个排列的实现。今天我们继续,讲一个排序:合并排序。
1.合并排序
基本思想就是先将n含有个元素的集合分成n/2个元素的子集合,分别对两个子集合进行合并排序,最后将排好序的子集合合并。我用一张实例图来概括一下。
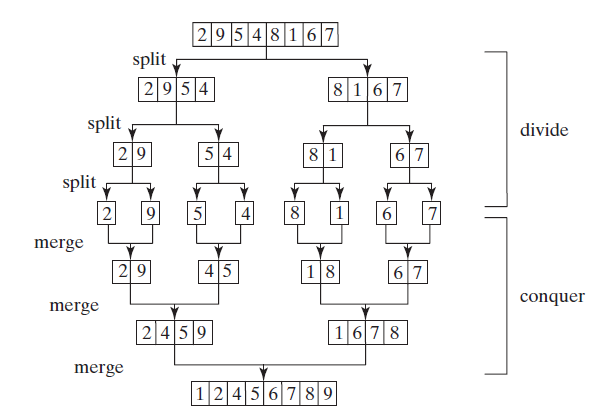
待排序集合为{2,9,5,4,8,1,6,7},首先将这个集合左右分解成两个子集合{2,9,5,4},{8,1,6,7},直到集合中的元素为一个(只有一个元素当然是已排好的)。再依次将两个已排序的子集合合并。最近在看的一部算法书中强调软件工程的API形式,即先API,再实现。那我也来试写下此算法的API。
合并排序的API
| void mergeSort(Comparable[] list) | 算法的入口 |
| void mergeSort(Comparable[] list, int low, int high) | 排序从low到high的元素 |
| void merge(Comparable[] list, int low, int mid, int high) | 在mergeSort中调用,将子集合[low...mid]和[mid+1...high]合并 |
我们先声明一个临时数组来辅助存储元素,而不在用每次合并时新声明一个数组。
private static Comparable[] tmp;
这样核心算法的实现就简单了,如下
 mergeSort
mergeSort
这里要注意下merge方法头同样是用private修饰的,因为只有mergeSort才能调用它,对于类外肯定是隐藏的(面向对象的封装属性)。
 merge
merge
1 private static void merge(Comparable[] list, int low, int mid, int high) 2 { 3 4 int i = low, //第一个数组的下标 5 j = mid + 1; //第二个数组的下标 6 for(int k = low; k <= high; k++) //临时数组赋值 7 { 8 tmp[k] = list[k]; 9 } 10 11 for(int k = low; k <= high; k++) 12 { 13 if(i > mid) //第一个数组已经比较完,只留下第二个数组的元素 14 list[k] = tmp[j++]; 15 else if(j > high) //第二个数组已经比较完,只留下第一个数组的元素 16 list[k] = tmp[i++]; 17 else if(tmp[j].compareTo(tmp[i]) == -1) // 第二个数组当前指向的元素大于第二个数组当前指向的元素 18 list[k] = tmp[j++]; 19 else 20 list[k] = tmp[i++]; 21 } 22 }
2.自底向上的合并排序
上面这种合并,被称为自顶向下的合并排序。其实只要将两个有序的集合合并成一个更大的有序集合就是合并操作。所以我们为什么不先合并那些微笑的集合,然后再成对合并得到的子集合。事实上这种方法比前面那种方法在代码上更加简洁。
所以我们先两两合并,然后再四四合并,...这样合并到顶。如果把元素个数不是2的幂的情况考虑进来的话,在最后一个合并中,第二个子集合一定小于或等于第一个子集合。
我把这个方法命名为mergeSortBU即为bottom-up mergesort,实现如下
 mergeSortBU
mergeSortBU
1 public static <E extends Comparable> void mergeSortBU(E[] list) 2 { 3 int n = list.length; 4 5 tmp = new Comparable[n]; 6 7 for(int size = 1; size < n; size = size + size) //size为子数组的大小,逐渐变大 8 { 9 for(int low = 0; low < n - size; low += size * 2) //low为子数组的索引,即每两个子数组的第一个元素下标 10 { 11 merge(list, low, low + size - 1, Math.min(low + size * 2 - 1, n - 1)); //将两个小数组合并成大小为size*2的数组 12 } 13 } 14 }
该方法完成子数组大小从小到大的合并,每一次进行的合并都是用循环划分成几个合并操作,即把两个小数组[low...low+size-1]和[low+size...low+size*2 -1](若最后一个数组有这么长的话)合并。
两种排序方法在进行比较和访问数组的次数和顺序会有所不同,关键还是元素个数是不是2的幂。你是希望像mergeSort()一样化整为零的解决方式,还是希望像mergeSortBU()那样循序渐进的解决方法呢?
3.改进
还可以对合并排序进行3项改进:加快小数组的排序速度,检测数组是否已经有序以及通过在递归中狡猾参数来避免数组复制。


