3.【几何基础】03 - 合同公理、平行公理、连续公理2022-01-22

4.【几何基础】04 - 比例和面积2022-01-22 5.【几何基础】05 - 笛沙格几何2022-01-29

1. 合同公理

1.1 线段和角的合同

　　关联定义了三大主角（点线面）的依附关系，顺序又限定了点在空间的次序（并间接影响线面的空间次序），现在还缺少对空间的度量。所谓度量就是对几何对象建立相等的概念，而相等的另一个等价说法就是教材上的“迁移”，“重合、相等”这样的概念本质上就是对象的动态关系，这样的关系我们称之为合同，记做 $=$ （为区别于常识上的 $=$ ，教材用的 $\equiv$ ）。所有对象的合同关系其实又可以拆解为线段合同与角合同，线段合同是对一维空间的度量（长度），而借助角合同可以把度量扩展到更高维（面积、体积）。

　　 $I I I .$ 合同公理

　　　　 $I I I_{1} .$ 直线 $a$ 上有两点 $A, B$ ，则 $a^{'}$ 上 $A^{'}$ 的任一侧都存在点 $B^{'}$ ，使得 $A B = A^{'} B^{'}$ 。

　　　　 $I I I_{2} .$ 假设 $A^{'} B^{'} = A B, A^{″} B^{″} = A B$ ，则有 $A^{'} B^{'} = A^{″} B^{″}$ 。

　　　　 $I I I_{3} .$ $B, B^{'}$ 分别在线段 $A C, A^{'} C^{'}$ 上，且 $A B = A^{'} B^{'}, B C = B^{'} C^{'}$ ，则有 $A C = A^{'} C^{'}$ 。

　　　　 $I I I_{4} .$ 对给定的角 $∠ (h, k)$ 和平面 $α^{'}$ 上的射线 $h^{'}$ ，则 $α^{'}$ 上 $h^{'}$ 的任一侧都存在唯一射线 $k^{'}$ 使得 $∠ (h, k) = ∠ (h^{'}, k^{'})$ 。

　　　　 $I I I_{5} .$ 任何角都与自己合同。

　　　　 $I I I_{6} .$ 假设 $A B = A^{'} B^{'}, A C = A^{'} C^{'}, ∠ B A C = ∠ B^{'} A^{'} C^{'}$ ，则有 $∠ A B C = ∠ A^{'} B^{'} C^{'}$ 。

　　需要提醒的是，为了使公理数量尽量少，公理中并没有直接给出合同关系的对称性和传递性。此时我们还只能认为“ $=$ ”是最一般的对象关系，然后通过公理推导出对称性和传递性。另外，由于线段（角）的定义中端点（边）的书写顺序不影响所表示的对象，这里也不区分 $A B$ 和 $B A$ 、 $∠ (a, b)$ 和 $∠ (b, a)$ 。

　　前三条公理是单独针对线段合同的， $I I I_{1}$ 给出了将线段迁移到直线上点的任一侧的可能性，其唯一性还需要后面的公理。 $I I I_{2}$ 给出了线段合同的一个性质，利用它可以直接证明线段合同的对称性和传递性，并继而证明线段与自己合同。 $I I I_{3}$ 其实说明了线段合同的可加性，这是度量最重要的一个性质。单纯的线段合同没有什么太多可讨论的（除非你想在直线上建立实数体系），它必须和角合同一起才能发挥威力。

　　再后两条公理是单独针对角合同的， $I I I_{4}$ 给出了角迁移到平面上射线任一侧的可能性和唯一性， $I I I_{5}$ 只给出了角与自身合同。结合这两个公理可知，如果 $∠ (a, b) = ∠ (a, b^{'})$ ，那么 $b, b^{'}$ 是一条射线，这个唯一性在后面很有用。角公理的唯一性和线段公理形成互补关系，它们结合之后才能发挥更大威力。但目前还得不出更多的结论，甚至连角合同的对称性和传递性都不能断言，以下论述中请千万注意这一点。这里先给出几个你已经熟知的定义：对于 $∠ (a, b)$ ， $∠ (a, b^{'})$ 称为它的邻补角， $∠ (a^{'}, b^{'})$ 称为它的对顶角，如果 $∠ (a, b) = ∠ (a, b^{'})$ ，称为直角。

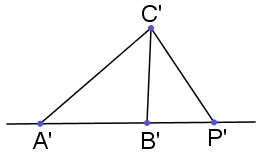
　　公理 $I I I_{6}$ 将线段合同与角合同相结合，合同关系也得以从一维上升到更高维。你可能发现它就是“三角形全等的边角边判定规则”中的一部分，由对称性其实还有 $∠ A C B \equiv ∠ A^{'} C^{'} B^{'}$ ，但是还需要证明 $B C = B^{'} C^{'}$ 。在射线 $B^{'} C^{'}$ 上取 $B^{'} D^{'} = B C$ （以下右图），则可知 $∠ C A B = ∠ D^{'} A^{'} B^{'}$ ，由角迁移的唯一性可知 $D^{'}, C^{'}$ 是重合的，即 $B C = B^{'} C^{'}$ 。结论中这种三条边和角都合同的三角形也成为合同的，记作 $△ A B C = △ A^{'} B^{'} C^{'}$ ，但要注意在角的对称性和传递性未证明之前，三角形合同也不一定满足这些性质。

　　公理 $I I I_{6}$ 选择的条件是非常独立的（角上线段与角本身独立），但又是构成三角形的自然方式，把它作为公理非常恰当。同样的方法其实还可以证明“角边角判定定理”，即已知 $∠ B = ∠ B^{'}, ∠ C = ∠ C^{'}, B C = B^{'} C^{'}$ ，则可判定 $△ A B C = △ A^{'} B^{'} C^{'}$ 。但要注意，如果给的条件是 $∠ A = ∠ A^{'}, ∠ B = ∠ B^{'}, B C = B^{'} C^{'}$ ，它是不同于“角边角”的条件的（没有三角和相等的概念），需要后续的论证。另外，同样的方法还可以证明线段迁移的唯一性，由唯一性就可以补齐可加性的同侧情况，至此线段合同的一般性质就算补齐了。

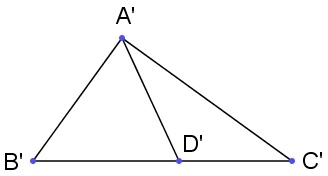
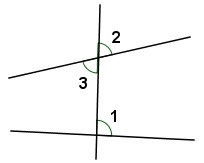
　　目前关于角合同，还未证明其对称性、传递性、可加性，而这些性质都是线段合同具有的，故证明中可考虑借助线段合同。先来看可加性，给定两组射线 $h, l, k$ 和 $h^{'}, l^{'}, k^{'}$ 和顶点 $O, O^{'}$ ，假设 $∠ (h, k) = ∠ (h^{'}, k^{'}), ∠ (l, k) = ∠ (l, k)$ ，且 $h, l$ 和 $h^{'}, l^{'}$ 同时在 $k, k^{'}$ 的同侧或异侧，目的是证明 $∠ (h, l) = ∠ (h^{'}, l)$ 。对在同侧的情况，可以假定 $l$ 在 $h, k$ 之间（以上右图），在 $h, h^{'}$ 取 $O A = O^{'} A^{'}$ 、在 $k, k^{'}$ 取 $O B = O^{'} B^{'}$ ，并设 $A B$ 交 $l$ 于 $C$ 。在 $B^{'} A^{'}$ 上取 $B^{'} C^{'} = B C$ ，可证明 $∠ (l, k) = ∠ C^{'} O^{'} B^{'}$ ，由角合同的唯一性可知 $l^{'}$ 与射线 $O^{'} C^{'}$ 重合，接下来不难证明结论。

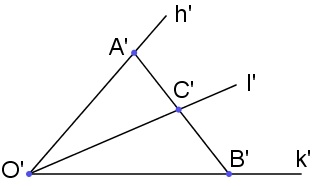
　　当 $h, l$ 和 $h^{'}, l^{'}$ 同时在 $k, k^{'}$ 的异侧时，证明非常类似，只要注意点证明射线重合及处理好平角就行。可加性的一个极端情况是，其中一个角是平角，要证明的其实是：已知两角合同，求证它们的补角也合同。以下取 $A B = A^{'} B^{'}, B C = B^{'} C^{'}, B D = B^{'} D^{'}$ 和 $∠ A B C = ∠ A^{'} B^{'} C^{'}$ （以下左图），要证 $∠ C B D = ∠ C^{'} B^{'} D^{'}$ 。结论的证明很简单，但要很好体会这几个结论中对线段合同可加性的运用。直接利用结论便可证明：对顶角相互合同。最后来构造直角，在射线 $O A$ 两侧作 $∠ B O A = ∠ C O A, O B = O C$ （以下右图），并设 $B C$ 交直线 $O A$ 于 $D$ 。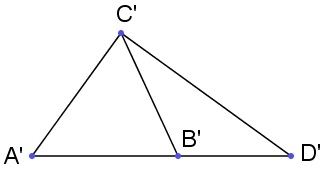若 $D$ 就是 $O$ 则 $∠ B O A$ 即为直角，不管 $D$ 在不在射线 $O A$ 上，都容易有 $∠ B O D = ∠ C O D$ ，接下来不难证明 $∠ B D O$ 就是直角。

　　角合同的对称性和传递性只能通过线段合同的性质证明，但由单纯的线段合同如何导出角合同？最简单的情形是这样的，利用 $I I I_{6}$ 不难发现，等腰三角形的两底角互相合同。复杂一点的情形，其实我们更想得到“边边边判定定理”，为了用到等腰三角形的结论，可以先退一步，考察有共边的两个三角形 $△ A B C, △ D B C$ ，其中 $A, D$ 在 $B C$ 两侧（以下左图）、且 $A B = D B, A C = D C$ 。利用等腰三角形的性质和角的可加性，容易证得两个三角形相互合同。

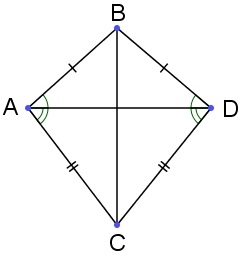
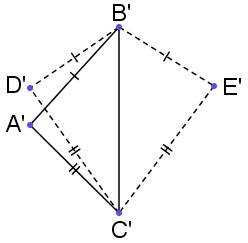
　　然后当 $△ A B C, △ A^{'} B^{'} C^{'}$ 三条边都相等时，将 $△ A B C$ 迁移到 $B^{'} C^{'}$ 的两侧得到 $△ D B^{'} C^{'}, △ E B^{'} C^{'}$ （以上右图）。利用刚才的结论， $∠ E C^{'} B^{'}$ 和 $∠ A^{'} C^{'} B^{'}, ∠ D C^{'} B^{'}$ 都合同，由唯一性便知射线 $C^{'} A^{'}, C^{'} D$ 重合。这就说明了 $∠ A C B = ∠ A^{'} C^{'} B^{'}$ ，从而 $△ A B C = △ A^{'} B^{'} C^{'}$ 。论证中注意哪些是一般合同、哪些是互相合同，千万不要随便交换等式两边。有了这个“边边边判定定理”之后，角合同的对称性和传递性也就显然了，至此角合同的基本性质也全部得到。

1.2 线段和角的比较

　　有“相等”（合同）就有“不相等”，顺序公理中对不相等的情况建立了序列，而这就方便了在度量中引入“大于”“小于”的概念。当两个角没有公共边时，必须通过合同迁移使得一条边重合，迁移后如果两条边都重合，两个角自然就是合同的。如果 $∠ 1$ 迁移后在 $∠ 2$ 内侧，则称 $∠ 1$ 小于 $∠ 2$ 、或 $∠ 2$ 大于 $∠ 1$ ，记作 $∠ 1 < ∠ 2$ 或 $∠ 2 > ∠ 1$ 。作为一种关系，它应当是确定的，也就是说随着各种迁移方法都有一致的结果。对于两个角 $∠ (a, b), ∠ (c, d)$ ，可以将 $∠ (c, d)$ 的一条边迁移到 $a$ 或 $b$ ，也可以将 $∠ (a, b)$ 迁移到 $c$ 或 $d$ 。

　　先来比较迁移到 $b, d$ 两种情形，假设 $c$ 被迁移到 $∠ (a, b) 外侧$ ，则在 $∠ (c, d)$ 内侧作 $∠ (d, a^{'}) = ∠ (a, b)$ （以下左图，可行性自证），由角合同的唯一性可知， $∠ (a, b)$ 迁移到 $d$ 的 $c$ 一侧时， $a$ 与 $a^{'}$ 重合。其它情况证明类似，总之，不管何种迁移方法，大、小于的结论都一致，这是一个良性的定义。这个定义也可以轻松地用在线段上，而且在此定义下，有这样简单的事实：两个线段（角）必有 $=, >, <$ 之一的关系。设三个线段（角）有关系 $a ⩾ b, b ⩾ c$ ，不难证明有传递性 $a ⩾ c$ ，等号成立充要条件是 $a = b, b = c$ 。

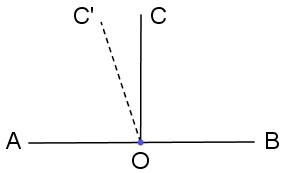
　　中学教材中规定：大于直角的角叫钝角，小于钝角的角叫锐角。不过在这里我们先要证明“直角”是一个确定的角，也就是说直角都互相合同。假设直线 $A B$ 上有 $∠ A O C = ∠ B O C$ （以上右图），则它们都是直角。再假设其它直角被迁移到射线 $O A$ 的 $C$ 这一侧时，另一条射线为 $O C^{'}$ ，则有 $∠ A O C^{'} = ∠ B O C^{'}$ 、且它们都是直角。如果 $O C^{'}$ 在 $∠ A O C$ 内侧，则有关系式 $∠ A O C^{'} < ∠ A O C = ∠ B O C < ∠ B O C^{'}$ ，这显然与 $∠ A O C^{'} = ∠ B O C^{'}$ 矛盾。当 $O C^{'}$ 在 $∠ B O C$ 内侧时，也有同样的矛盾，故只有 $O C$ 与 $O C^{'}$ 重合，所有直角都合同。

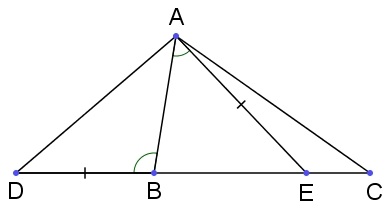
　　三角形的三个角也叫它的内角，每个角的补角也叫外角，现在来比较外角与其它两个内角的关系。假设 $△ A B C$ 中有 $∠ A B D ⩽ ∠ A$ （下图），则可以在 $∠ A$ 内部（或合同）作 $∠ B A E = ∠ A B D$ 。取 $D$ 使得 $B D = A E$ ，可证 $△ A B E = △ B A D$ ，所以 $∠ B A D = ∠ A B E$ ，但 $∠ B A D$ 显然与 $∠ B A E$ 不互补，导出矛盾。这就是说必然有 $∠ A B D > ∠ A$ ，同样也有 $∠ A B D > ∠ C$ ，即外角大于其它两个内角，该结论称为外角定理。

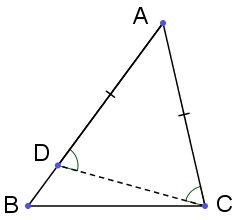
　　外角定理非常有用，它可以推导出一系列直观的结论。之前说过，等腰对应等角，当三角形两条边不相等时，不妨设 $A B > A C$ （以下左图）。在 $A B$ 上取 $A D = A C$ ，则有关系 $∠ B < ∠ A D C = ∠ A C D < ∠ A C B$ ，这个结论可以总结为：三角形中长边对应的角也大。反过来，如果知道两个角的关系呢？其实因为线段的关系只有三种，如果逆命题不成立，必然会导致矛盾。所以至此，完整结论可以叙述为：三角形中边长排序和对应角的排序总是一致的。这也是一个很有用的结论，比如在 $△ A B C$ 中（以下右图），延长 $B A$ 使得 $A D = A C$ ，由 $∠ D < ∠ B C D$ 可知 $B C < A D = A B + A C$ ，即三角形两边和大于第三边。

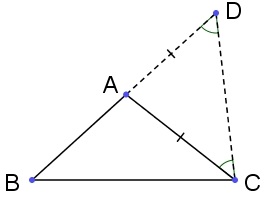
　　由于现在还没有三角形三角和的概念，之前的“角边角判定定理”还有一个变异的“角角边”的情况需要证明，即已知 $∠ A = ∠ A^{'}, ∠ B = ∠ B^{'}, B C = B^{'} C^{'}$ ，求证 $△ A B C = △ A^{'} B^{'} C^{'}$ 。其实就只要证 $∠ C = ∠ C^{'}$ ，否则假设 $∠ C > ∠ C^{'}$ ，把 $∠ C^{'}$ 迁移到射线 $C B$ 的 $A$ 侧、并交 $A B$ 于 $D$ （以下左图）。先证得 $△ D B C = △ A^{'} B^{'} C^{'}$ ，从而 $∠ B D C = ∠ A^{'} = ∠ A$ ，这与外角定理矛盾，故“角角边判定定理”也成立。

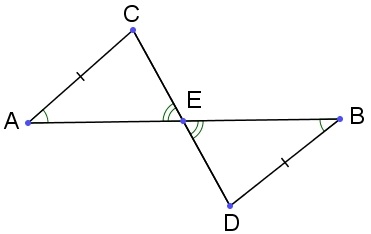
　　在这个判定定理下，我们可以把任意线段二等分。对给定线段 $A B$ （以上右图），在 $A B$ 两侧分别作 $∠ C A B = ∠ D B A$ 、并取 $A C = B D$ ，设 $C D$ 交直线 $A B$ 于 $E$ 。由判断定理可知 $△ E A C = △ E B D$ ，从而 $A E = B E$ ，不难证明 $E$ 一定在 $A, B$ 之间，它就是线段 $A B$ 的二等分点。继而我们还可以把任意角 $∠ A O B$ 二等分，只需取 $A O = B O$ 并取线段 $A B$ 的中点 $C$ ，容易证明射线 $O C$ 就是 $∠ A O B$ 的角平分线。

1.3 图形的合同

　　从两点的合同到三角形的合同，其实描述的是同一个概念，即图形的运动。因此我们可以把合同的概念推广到更一般的图形中，这里我们把图形定义为空间中的一个点集 $Φ$ ，在同一平面的图形也叫平面图形。两个图形 $Φ, Φ^{'}$ 合同其实就是通过运动能互相重合，这就要求 $Φ, Φ^{'}$ 的点集之间可以建立一一对应，在此对应下，共线、共面、共侧关系保持一致，而且相应的线段、角度也都合同。在欧几里得空间中，我们有这样的印象：只要两个图形点的相互距离保持不变，这个图形的形状也不变，我们自然想问：线段合同是不是图形合同的充要条件？

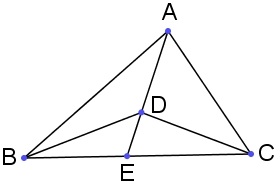
　　首先由上面的“三角形两边和大于第三边”，不难证明三点共线即顺序关系一定是保持的，进而也不难推断出所有的共线和顺序关系保持一致。再根据三角形的“边边边判定定理”，也容易知道所有对应角也都合同。现在来证共面性也是一致的，即如果 $D$ 在平面 $A B C$ 上（以下左图， $A, B, C$ 不共线）， $D^{'}$ 也一定在平面 $A^{'} B^{'} C^{'}$ 上。如果 $D$ 与 $A, B, C$ 中某两点共线，结论是显然的。若不共线则一定可以选定点 $A$ ，使得线段 $A D$ 或其延长线与线段 $B C$ 相交（自行证明并分类讨论），设交点为 $E$ 。在 $B^{'} C^{'}$ 上作对应的合同点 $E^{'}$ ，讨论图形 ${A, D, E}$ 与 $A^{'}, D^{'}, E^{'}$ 的合同性，则容易知道 $D^{'}$ 一定也在直线 $A^{'} E^{'}$ 上，即在平面 $A^{'} B^{'} C^{'}$ 上，共面性保持一致。

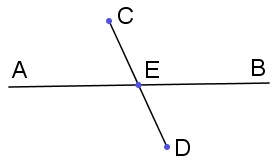
　　最后来看共侧关系，如果点 $C, D$ 在直线 $A B$ 两侧（以上右图），设线段 $C D$ 与直线 $A B$ 交于 $E$ 。在直线 $A^{'} B^{'}$ 上作合同的点 $E^{'}$ ，讨论图形 ${C, D, E}$ 与 ${C^{'}, D^{'}, E^{'}}$ 的合同性，不难知道 $C^{'}, D^{'}$ 也在 $A^{'} B^{'}$ 两侧。这就证明了平面上直线两侧的关系保持不变，同样也可以证明空间中平面两侧的关系也不变。至此我们便证明了两个图形合同的充要条件是对应的线段全部合同。

　　在欧几里得空间中，我们知道一维、二维、三维图形的运动其实分别由两个不同点、三个不共线点四个不共面点确定（以下称基础点）。也就是说如果知道了运动后基础点的位置，其它的点都能唯一构造出来。或者换个说法，对于包含基础点的两个合同图形 $Φ, Φ^{'}$ ，当在 $Φ$ 上扩充点 $P$ 时，也一定能在 $Φ^{'}$ 上扩充唯一的 $P^{'}$ ，且扩充后图形仍然合同。在一维空间（直线）中，利用线段的可加性，不难构造出唯一的扩充点 $P^{'}$ ，请自行证明。对于更高维的情况，都需要论证新扩充点的存在性（与所有点的线段保持合同），以及唯一性（一般构造过程即说明了唯一性）。

　　在二维空间（平面）中，如果 $P$ 与 $Φ$ 中某两点 $A, B$ 共线，则先在 $Φ^{'}$ 的直线 $A^{'} B^{'}$ 上构造合同的唯一点 $P^{'}$ （以下左图），然后利用判定定理不难证明： $P^{'}$ 与直线外任意点 $C^{'}$ 都满足 $P^{'} C^{'} = P C$ 。当 $P$ 不与任何两点共线时，可以构造过点 $P$ 的直线交两条已知直线于 $P_{1}, P_{2}$ （以下右图，自行证明存在性）。则可以先将 $P_{1}, P_{2}$ 扩充到 $Φ$ 中，根据刚才共线的讨论， $Φ^{'}$ 可以加进的扩展点 $P_{1}^{'}, P_{2}^{'}$ 。而这时 $P$ 与新图形 $Φ$ 中的 $P_{1}, P_{2}$ 共线，也自然能在 $Φ^{'}$ 中扩充进对应的 $P^{'}$ 。不过要注意，这时的 $P^{'}$ 对于原图 $Φ^{'}$ 来说只是存在，还需证明其唯一性。这时再把刚才的 $P_{1}, P_{2}$ 添加进来，反过来根据合同关系证明 $P_{1}^{'}, P_{2}^{'}, P^{'}$ 共线即可。

　　在三维空间中，如果 $P$ 与 $Φ$ 中的某两点共线（或三点共面），刚才的论述在线上（或面上）的唯一扩充是存在的，与线（面）外点线段合同用上段同样的方法证明。如果 $P$ 不在任何已知直线（平面）上，同样可以构造某条过 $P$ 且与已知线面相交至少两次的直线，接下来类似地证明 $P^{'}$ 存在和唯一性。这几段论述，进一步验证了，图形合同的本质就是图形的运动。

2. 平行公理

　　前面的三套公理定义了点、线、面的基本关系，它们可以构成一套非常自洽的系统。在前面的论述中，你可能注意到，很多问题的描述都依赖交点的存在，而尽量避免讨论不相交的情况，平行公理就是对不相交作了一定限制。当同一平面上的两条直线没有交点、直线或平面与另一个平面没有交点时，都称它们是平行的（注意说直线平行意味着一定共面），记做 $a ∥ b$ 、 $a ∥ α$ 或 $α ∥ β$ 。我们需要讨论平行线（面）的存在性以及其数量，还要研究平行的判定定理及性质。

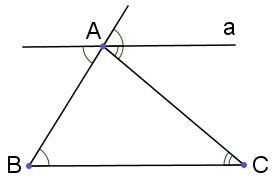
　　先来看最简单的情形，考虑同一平面上的直线 $a$ 和直线外一点 $A$ ，研究平面上过 $A$ 且与 $a$ 平行的直线。先来看一些你中学时熟悉的概念，过 $A$ 作一条与 $a$ 相交的直线 $c$ 和任意直线 $b$ （以下左图），其中 $∠ 1$ 与 $∠ 2$ 互为同位角， $∠ 1$ 与 $∠ 3$ 互为内错角，而且显然 $∠ 2 = ∠ 3$ 。如果作直线 $b$ 时让 $∠ 1 = ∠ 2$ 或 $∠ 1 = ∠ 3$ ，不难用反正法证明 $a, b$ 是平行的（使用外角定理）。这就证明了平面上过直线外固定点的平行线的存在性，它是直线平行的一个判定定理。

　　这个判定定理的逆命题是否成立呢？或者说除了直线 $b$ 是否还有其它平行线呢？这个问题的答案从之前的公理中是无法得知的，只能用以下平行公理作限制，结合平行公理和刚才的存在性，便可知平行线的唯一性。这样的假设符合欧几里得空间的常识，而且在后续的问题讨论中起到非常重要的作用，它在欧几里得的《几何原理》中也是被作为著名的“第五公设”而提出的。历史上很多人尝试去证明第五公设，但要么无功而返、要么在证明中隐晦地使用到了第五公设的推论。后来人们构造出了不满足第五公设的几何体统，才认识到它的独立性，并由此对不同的几何进行了深入的讨论。

　　在有平行公理的情况下，刚才构造的直线 $b$ 便是唯一的平行线，或者换个说法：平面上如果有 $a ∥ b, a ∥ c$ ，则 $b, c$ 重合或 $b ∥ c$ 。平行线的唯一性，使得由平行也能反推到“同位角相等”和“内错角相等”，这是个很有用的结论。比如在 $△ A B C$ 中（以上右图），过点 $A$ 作 $B C$ 的平行线 $a$ ，显然有 $∠ 3 = ∠ 1 = ∠ B$ 和 $∠ 2 = ∠ C$ 。这时我们可以说：三角形三角和为一个平角，或者说三角形的外角等于另外两内角之和，它可以看成是外角定理的加强版。在这个结论下，便可以定义并讨论圆的一些性质，这些就是初等几何的内容了。

　　 $I V .$ 平行公理

　　　　 $I V .$ （欧几里得公理）设直线 $a$ 和其外一点 $A$ 确定平面 $α$ ，则 $α$ 上至多有一条过 $A$ 且不与 $a$ 相交的直线。

　　现在把对平行的讨论放到三维空间中。已知平面 $α$ 和平面外一点 $A$ ，对 $α$ 上的任一条直线 $a$ ，都存在唯一过 $A$ 的直线 $a^{'}$ 与 $a$ 平行。设 $A, a$ 确定的平面是 $β$ ，则 $α, β$ 相交于 $a$ ，故如果 $a^{'}$ 与 $α$ 有交点，一定也在 $a$ 上，这是不可能的，从而 $a^{'} ∥ α$ 。这就证明了过 $A$ 与 $α$ 平行的直线的存在性，同时证明过程还给出了直线与平面平行的一个判定定理，即如果 $a$ 与平面 $α$ 上的一条直线平行，则 $a$ 在 $α$ 上或 $a ∥ α$ 。这个判定定理换个说法就是，如果 $a ∥ b$ ，则过 $b$ 的任意平面要么过 $a$ 、要么与 $a$ 平行。反之如果有 $a ∥ α, a ∥ β$ ，且 $α, β$ 交于 $b$ ，取 $b$ 上一点 $A$ ，并设平面 $(A, a)$ 分别交平面于 $b^{'}, b^{″}$ 。由于 $a$ 与 $b^{'}, b^{″}$ 都平行，故只能是 $b^{'}, b^{″}$ 重合于 $b$ ，所以有 $a ∥ b$ 。

　　刚才我们用到这样一个简单的结论：如果 $a ∥ α$ ，则过的 $a$ 平面 $β_{1}, β_{2}, \dots$ 与 $α$ 的交线 $b_{1}, b_{2}, \dots$ 都与 $a$ 平行。其实由 $β_{i}$ 间交线的唯一性，可知 $b_{i}$ 之间没有交点，从而 $b_{1}, b_{2}, \dots$ 互相平行。对这个结论，我们有两点扩充。其一是该命题的逆命题，即如果 $α$ 上有 $b ∥ c$ ，且分别过 $b, c$ 的平面 $β, γ$ 相交于直线 $a$ ，则一定有 $a ∥ α$ 。其实由 $b ∥ c$ 得到 $c ∥ β$ ，从而 $c ∥ a$ ，再而 $a ∥ α$ 。另一个扩充是，如果 $a ∥ b, a ∥ c$ ，能否推出 $b ∥ c$ ？其实由 $a ∥ b$ 知 $b$ 平行于平面 $(a, c)$ ，取 $c$ 上一点 $C$ 、并设平面 $(C, b)$ 交平面 $(a, c)$ 于 $c^{'}$ ，这时应当有 $a ∥ c^{'}$ ，由唯一性知 $c^{'}, c$ 重合，即 $b ∥ c$ 。

　　以上两段是直线与平面平行的一些判定定理和性质，现在回到构造平行线的现场。设 $α$ 上有两条相交直线 $a, b$ ，在 $α$ 外一点 $A$ 分别作 $a^{'} ∥ a, b^{'} ∥ b$ ，不难证明 $a^{'}, b^{'}$ 是不同的直线，也就是说过点 $A$ 与 $α$ 平行的直线不唯一。记 $a^{'}, b^{'}$ 组成的平面为 $β$ ，如果 $β$ 与 $α$ 有交线 $c$ ，则应该有 $a^{'} ∥ c, b^{'} ∥ c$ ，从而 $a^{'} ∥ b^{'}$ ，这与 $a^{'}, b^{'}$ 交于 $A$ 矛盾。也就是说 $α ∥ β$ ，我们构造了一个过点 $A$ 且与 $α$ 平行的平面。

　　其实对于任意过 $A$ 且与 $α$ 平行的平面 $β^{'}$ ，可知 $a^{'}, b^{'}$ 都是平面 $(A, a), (A, b)$ 与 $β^{'}$ 的交线，这说明 $β^{'}, β$ 重合，平行面是唯一的。进而其实还说明，任何过点 $A$ 且与 $α$ 平行的直线，都在平面 $β$ 上。两平行平面上的任意两条线没有交点，所以如果不限定在一个平面上，不相交直线将有无数条，不能保证平行线的唯一性。另外也容易证明，如果 $α ∥ β, α ∥ γ$ ，则 $β, γ$ 重合或平行。

3. 连续公理

　　至此，公理能建立起来的几何系统已经相当完整了，但还不完全等价于欧几里得几何空间，我们需要在点集上作进一步的限制。在此之前，公理的讨论都只针对有限的对象，而刻意避开了无穷的概念，但在这里就必须面对“直线的上的所有点”这样的问题。顺序公理要求直线上的点集构成一个全序集，而连续公理的目的是把它限制为与实数集同构的全序集。

　　 $V .$ 连续公理

　　　　 $V_{1} .$ （阿基米德公理）给定线段 $A B, C D$ ，从点 $A$ 开始向 $B$ 的方向作收尾交替、且都与 $C D$ 的合同的线段，则有限次后必将超过点 $B$ 。

　　　　 $V_{2} .$ （完备公理）任一直线上的点集都不能再扩充。

　　实数有两个重要的特点，一个是两个点的距离不会“无限远”，这个特点在抽象代数中就叫“阿基米德公理”。这个公理限定了直线上点集的上限，它必须同构与实数集的一个子集。实数的另一个特点就是其完备性，也就是说实数集里没有空隙，而完备公理则要求直线点集只能与实数集同构。当然，对于一般的讨论，完备公理是有点冗余的，选择一个合适的子集也能得到比较完整的直观系统。甚至连阿基米德公理也可以排除在一般几何的讨论之外，彻底将几何与“数”分割开来。其实教材的主要篇幅，都摒弃了连续公理，而纯粹地讨论空间关系（非阿基米德几何）。

　　连续公理都是限定在直线上的，其实它们在三维空间中也成立，下面来证明完备公理的空间形式。先来看任意已有的平面 $α$ ，其上必定有三个不共线的点 $A, B, C$ （以下左图），现在试图在 $α$ 上添加新点 $P$ 。在某条边上任取旧点 $D$ ，已知直线 $D P$ 与 $△ A B C$ 必然还有一个交点 $E$ ，但旧点 $D, E$ 确定的直线不应当能添加新点 $P$ 。这就导致矛盾，故已有平面上一定不能再添加新点。再假设空间中可以添加新点 $P$ ，任选不共面的旧点 $A, B, C, D$ （以下右图），并设平面 $(A, B, P)$ 与平面 $(B, C, D)$ 交于直线 $B E$ 。由于面 $(B, C, D)$ 是已知面，故点 $E$ 也是旧点，平面 $(A, B, E)$ 也是已知面，其中不能添加新点 $P$ 。这个矛盾就说明了三维空间中也不能添加新点，空间中完备定理得证。