| 习题 118:求n!位数(ct15)★ 题目描述:
求n!的位数,例如1!=1,1位;5!=120,3位。
输入:
本题有多组测试数据,每组一行整数n<=1e6。输入以一个任意负数结束。
输出:
对于每一组测试数据n,输出一行一个整数,代表n!的位数。
样例输入:
1
5
-1
样例输出:
1
3
其它信息:
Contest15竞赛题目
经典问题
难度:Very Easy
|
常规思路就是先求出n!的值,然后log10(n!)就是n!位数。
我们先来用常规方法求一下n!:
public class FactorialClass {
//递归
long recursive(int n){
if(n<=1)
{
return 1;
}
else
{
return n*recursive(n-1);
}
}
//非递归
long non_recursive(int n){
long product=n;
if(n<=0)
{
return 1;
}
for(int i=n-1;i>1;i--)
{
product*=i;
}
return product;
}
}
public class FactorialTest {
/**
* @Version 1.6 2009/10/05
* @author Eduardo
*/
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
FactorialClass value=new FactorialClass();
int n;
System.out.println("请输入n的值:");
while(cin.hasNextInt())
{
n = cin.nextInt();
if(n<0)break;
System.out.println("n的阶乘为:"+value.non_recursive(n));
System.out.println("阶乘的位数为 :"+((int)Math.log10(value.non_recursive(n))+1));
System.out.println("输入一个正数【继续】,输入任意负数【退出】");
} }
} |
从输出结果看:

当n取21时,n!的值溢出了,即超过了long的取值范围,这也就表明常规解法不能求出大数值的n!。
上Baidu查询解决办法,得知斯特林公式可以解决问题:
|
维基百科
斯特灵公式是一条用来取n阶乘近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特灵公式十分好用,而且,即使在n很小的时候,斯特灵公式的取值已经十分准确。
公式为:
 (1) (1)
这就是说,对于足够大的整数n,这两个数互为近似值。更加精确地:
 (2) (2)
或
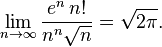 (3) (3) |
我们把公式(1)推导一下:
ln(n!)=0.5*ln(2*PI*n)+n*ln(n/e)
=0.5*ln(2*PI*n)+n*ln(n)-n
根据换底公式ln(n)/ln(10)=log10(n)得:
log10(n!)=(0.5*ln(2*PI*n)+n*ln(n)-n)/log10(n)
下面我就用Java表示求阶乘近似位数公式。
Math类有两个静态属性:E和PI。E代表数学中的e 2.7182818,而PI代表派pi 3.1415926。
| 类型 |
属性名 |
描述 |
| static double |
E |
比任何其他值都更接近 e(即自然对数的底数)的 double 值。 |
| static double |
PI |
比任何其他值都更接近 pi(即圆的周长与直径之比)的 double 值。 |
Math类有很多静态方法:求三角函数、反三角函数、指数函数、幂数函数、绝对值等等。下面只列举部分方法,其他方法参见JDK帮助文档。
| 类型 |
方法名 |
描述 |
| static double |
log(double a) |
返回 double 值的自然对数(底数是 e)。 |
| static double |
log10(double a) |
返回 double 值的底数为 10 的对数。 |
| static double |
log1p(double x) |
返回参数与 1 之和的自然对数。 |
| 类型 |
方法名 |
描述 |
| static double |
ceil(double a) |
返回最小的(最接近负无穷大)double 值,该值大于等于参数,并等于某个整数。 |
由于log10(n!)是double所以要向上取整:
log10(n!)=(int)(Math.ceil((0.5*Math.log(2*n*Math.PI)+n*Math.log(n)-n)/Math.log(10)))
import java.io.*;
import java.util.*;
public class Stirling {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
int n;
while(cin.hasNextInt()){
n = cin.nextInt();
if(n<0)break;
if(n==1||n==0)System.out.println(1);
else System.out.println((int)(Math.ceil((0.5*Math.log(2*n*Math.PI)+n*Math.log(n)-n)/Math.log(10))));
}
}
}
|
这样既可满足习题的要求了。




 (1)
(1) (2)
(2)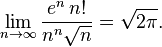 (3)
(3)

