二叉树的二叉链表存储表示如下
//二叉树的二叉链表存储表示
typedef struct BiTNode {
char data;//结点数据域
struct BiTNode* lchild, * rchild;//左右孩子指针
}*BiTree;
根据括号表示法的字符串创建树(括号里的表示括号前结点的子结点,‘,’号左边是左子结点,右边是右子结点)
比如:a(b(d,e),c(f,g(h,i)))
表示的则是
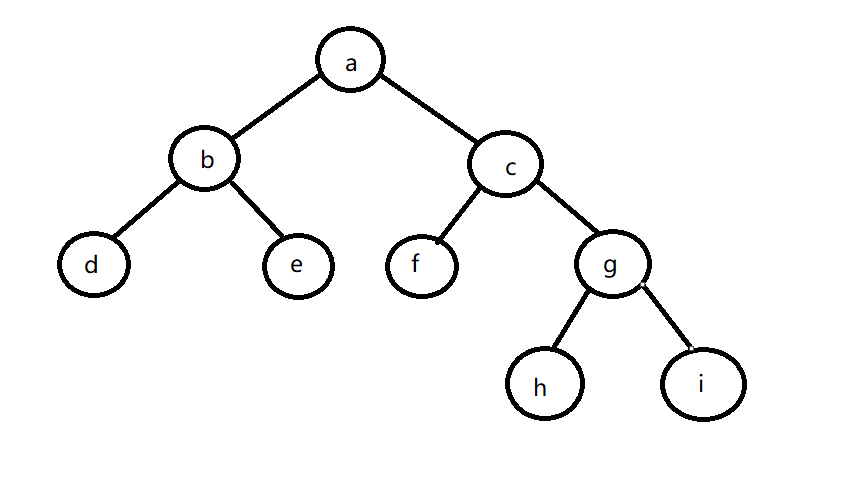
//创建树
void CreateBiTree(BiTree& T)
{
stack<BiTNode*> s;//用于确定需要操作的结点
BiTNode* p=NULL;
int i = 0;
bool child_Direct;//0表示左子结点,1表示右子结点
//按先序次序输入二叉树中结点的值(一个字符),创建二叉链表表示的二叉树T
string TreeStr;
cin >> TreeStr;
while (TreeStr[i] != '\0') {
switch (TreeStr[i])
{
case'('://左子结点
s.push(p);
child_Direct = false;
break;
case')':
s.pop();
case','://右子结点
child_Direct = true;
break;
default:
p = new BiTNode;
p->data = TreeStr[i];
p->lchild = p->rchild = NULL;
if (T == NULL)//若根节点为空则p指向根节点
T = p;
else {
if (!child_Direct)
s.top()->lchild = p;
else
s.top()->rchild = p;
}
break;
}
i++;
}
}
非递归先序、中序、后序遍历
先序:
void PreOrderTraverse(BiTree T) {
stack<BiTNode*> s;
BiTNode* p = T, * q = new BiTNode();
while (p != NULL || !s.empty()) {
if (p)//p非空
{
cout << p->data;
s.push(p);//根指针入栈
p = p->lchild;//遍历左子树
}
else {
p = s.top();
s.pop();
p = p->rchild;//遍历右子树
}
}
}
中序:
//中序遍历
void InOrderTraverse(BiTree T) {
stack<BiTNode*> s;
BiTNode* p = T, * q = new BiTNode();
while (p != NULL || !s.empty()) {
if (p)//p非空
{
s.push(p);//根指针入栈
p = p->lchild;//遍历左子树
}
else {
p = s.top();
s.pop();
cout << p->data;
p = p->rchild;//遍历右子树
}
}
}
后序:
//后序遍历
void PostOrderTraverse(BiTree T) {
BiTNode* p = T, * r = NULL;
stack<BiTNode*> s;
while (p != NULL || !s.empty()) {
if (p != NULL) {//走到最左边
s.push(p);
p = p->lchild;
}
else {
p = s.top();
if (p->rchild != NULL && p->rchild != r)//右子树存在,未被访问
p = p->rchild;
else {
s.pop();
cout << p->data;
r = p;//记录最近访问过的节点
p = NULL;//节点访问完后,重置p指针
}
}//else
}//while
}
完整代码
#include <iostream>
#include <stack>
#include <string>
using namespace std;
//二叉树的二叉链表存储表示
typedef struct BiTNode {
char data;//结点数据域
struct BiTNode* lchild, * rchild;//左右孩子指针
}*BiTree;
void Initial(BiTree& T) {
T = new BiTNode;
T = NULL;
}
//创建树
void CreateBiTree(BiTree& T)
{
stack<BiTNode*> s;//用于确定需要操作的结点
BiTNode* p=NULL;
int i = 0;
bool child_Direct;//0表示左子结点,1表示右子结点
//按先序次序输入二叉树中结点的值(一个字符),创建二叉链表表示的二叉树T
string TreeStr;
cin >> TreeStr;
while (TreeStr[i] != '\0') {
switch (TreeStr[i])
{
case'('://左子结点
s.push(p);
child_Direct = false;
break;
case')':
s.pop();
case','://右子结点
child_Direct = true;
break;
default:
p = new BiTNode;
p->data = TreeStr[i];
p->lchild = p->rchild = NULL;
if (T == NULL)//若根节点为空则p指向根节点
T = p;
else {
if (!child_Direct)
s.top()->lchild = p;
else
s.top()->rchild = p;
}
break;
}
i++;
}
}
//以括号表示法输出二叉树
void DispBTNode(BiTNode *&b)
{
if (b != NULL)
{
cout<<b->data;
if (b->lchild != NULL || b->rchild != NULL)
{
cout<<"(";
DispBTNode(b->lchild);
if (b->rchild != NULL) cout<<(",");
DispBTNode(b->rchild);
cout<<")";
}
}
}
#pragma region 递归遍历
//先序
void PreOrderTraverseR(BiTree T) {
if (T != NULL) {
cout << T->data;
PreOrderTraverseR(T->lchild);
PreOrderTraverseR(T->rchild);
}
}
//中序
void InOrderTraverseR(BiTree T) {
if (T != NULL) {
InOrderTraverseR(T->lchild);
cout << T->data;
InOrderTraverseR(T->rchild);
}
}
//后序
void PostOrderTraverseR(BiTree T) {
if (T != NULL) {
PostOrderTraverseR(T->lchild);
PostOrderTraverseR(T->rchild);
cout << T->data;
}
}
#pragma endregion
#pragma region 非递归遍历
//先序遍历
void PreOrderTraverse(BiTree T) {
stack<BiTNode*> s;
BiTNode* p = T, * q = new BiTNode();
while (p != NULL || !s.empty()) {
if (p)//p非空
{
cout << p->data;
s.push(p);//根指针入栈
p = p->lchild;//遍历左子树
}
else {
p = s.top();
s.pop();
p = p->rchild;//遍历右子树
}
}
}
//中序遍历
void InOrderTraverse(BiTree T) {
stack<BiTNode*> s;
BiTNode* p = T, * q = new BiTNode();
while (p != NULL || !s.empty()) {
if (p)//p非空
{
s.push(p);//根指针入栈
p = p->lchild;//遍历左子树
}
else {
p = s.top();
s.pop();
cout << p->data;
p = p->rchild;//遍历右子树
}
}
}
//后序遍历
void PostOrderTraverse(BiTree T) {
BiTNode* p = T, * r = NULL;
stack<BiTNode*> s;
while (p != NULL || !s.empty()) {
if (p != NULL) {//走到最左边
s.push(p);
p = p->lchild;
}
else {
p = s.top();
if (p->rchild != NULL && p->rchild != r)//右子树存在,未被访问
p = p->rchild;
else {
s.pop();
cout << p->data;
r = p;//记录最近访问过的节点
p = NULL;//节点访问完后,重置p指针
}
}//else
}//while
}
#pragma endregion
int main()
{
BiTree b;
Initial(b);
//创建树
CreateBiTree(b);
//先序遍历
cout << "先序遍历:";
PreOrderTraverse(b);
cout << endl;
//中序遍历
cout << "中序遍历:";
InOrderTraverse(b);
cout << endl;
//后序遍历
cout << "后序遍历:";
PostOrderTraverse(b);
}
程序示例:





