【CV】Nerf中体素渲染的离散公式推导

在文章《NeRF: representing scenes as neural radiance fields for view synthesis》中体素渲染的连续形式为

在文章中给出了其离散形式为

实际上这里的离散形式并不是将积分直接离散化，而是通过把路径上的density和color设定为分段常数，如下图所示

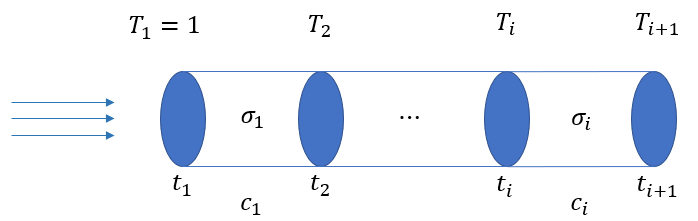
于是先计算\(T\),

\[\begin{aligned} T_i=T(t_i)&=\exp(-\int_{0}^{t_i}\sigma(t)dt) \\ &=\exp(-\sum_{j=1}^{i-1}\int_{t_{j}}^{t_{j+1}}\sigma(t)dt) \\ &=\exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j), \end{aligned} \]

其中\(\delta_i=t_{i+1}-t_i\)。然后计算\(C\),

\[\begin{aligned} C(\mathbf{r})=\int_0^{t_{N+1}}T(t)\sigma(t)\mathbf{c}(t)dt&=\sum_{i=1}^N\int_{t_i}^{t_{i+1}}T(t)\sigma(t)\mathbf{c}(t)dt \\ &=\sum_{i=1}^N\int_{t_i}^{t_{i+1}}\exp(-\int_0^t\sigma(s)ds)\sigma_i\mathbf{c}_idt \\ &=\sum_{i=1}^N\int_{t_i}^{t_{i+1}}T_i\exp(-\int_{t_i}^t\sigma(s)ds)\sigma_i\mathbf{c}_idt \\ &=\sum_{i=1}^NT_i\sigma_i\mathbf{c}_i \int_{t_i}^{t_{i+1}}\exp(-\sigma_i(t-t_i))dt \\ &=\sum_{i=1}^NT_i\sigma_i\mathbf{c}_i\cdot-\frac1{\sigma_i}\exp(-\sigma_i(t-t_i))\big|_{t_i}^{t_{i+1}} \\ &=\sum_{i=1}^NT_i\mathbf{c}_i\cdot(1-\exp(-\sigma_i\delta_i)). \end{aligned} \]

就跟原文中一样啦。