YOLOv1

目录

• 论文信息
• 前言
• Introduction
• Unified Detection
  • Network Design
  • Training
  • Inference
  • Limitations of YOLO
• Experiments
  • VOC 2007 Error Analysis
  • Combining Fast R-CNN and YOLO
  • Generalizability: Person Detection in Artwork
• Conclusion

论文信息

Joseph Redmon, Santosh Divvala, Ross Girshick, and Ali Farhadi. You Only Look Once: Unified, Real-Time Object Detection. CVPR 2016.

http://arxiv.org/abs/1506.02640

前言

YOLOv1基本上可以被认定为神经网络新时代one stage的祖宗, 其创新点若干, 或者可以说作者在此新模型时(2015前后)并没有用受前任影响太多, 是一项开天辟地式的工作.

我本打算直接整理YOLO9000的内容, 但考虑到YOLOv1早晚要整理且当时阅读时自己能力有限可能并没有完全理解,便当复习重新看了一遍.

Introduction

作者从人类的glace说起, 我们看物体大多是只看一次(You Only Look it Once, YOLO for short)就会记得其特点, 因此作者希望以此文出发点构建一种新的模型.

当时的object detection模型大多是从classifier通过微调迁移过来. 以R-CNN为例是先通过proposal再进行classification, 对此结果的bbox和class进行refine. 这种pipeline方法是低速且难以优化的, 因为它将各部分分离.

作者提出一种简单的直接regression的方法, 此方法直接从各个pixel与bbox及class probability建立联系.

简易框架如图所示:

一个单卷积网从一系列box(后文会详细解释)产生bbox和class probability, YOLO再用全图直接对其进行优化. 这样做有以下几点好处:

1. 速度快, 不需要pipeline.
2. 利用全图信息, 不容易将bg信息分错.
3. 泛化性强, 可以从自然图像迁移到艺术图象检测中.

但YOLO精度还是不如当时的state-of-the-art水平, 且在小物检测仍有欠缺.

Unified Detection

此系统将图片划成\(S\ times S\)个grid, 当有物体的中心落到grid里时, 该grid cell就会对其有响应(牢记这一点).

每个grid cell都会预测\(B\)个bbox.

该bbox包含confidence score. 这个confidence score是根据预测类别和IOU综合确定的:

\[condience = Pr(Object) * IOU_{pred}^{truth} \]

这里的\(Pr(Object)\)是指预测该bbox内有物体的把握, 如果预测里面没有物体则其为0, 同时confidence score也为0.

同时该bbox也包含\(x, y, w, h\)即用来确定位置尺寸的信息, 在bbox regression的资料会有介绍.

每个grid cell同时还还预测\(C\)个class的probability - \(Pr(Class_i|Object)\), 很容易看出这是指在有物体的情况的条件概率. 每个grid cell只预测一个set的class probability(这便是本模型的缺陷 - 一个cell只能预测一个物体, 如果存在多个物体就会预测失败, 在后来的模型中解决了此问题.). 此set不受bbox的数量\(B\)的影响.

因此综合考虑我们得到复合confidence prediction, 并利用概率理论简化此结果:

\[Pr(Class_i|Object) * Pr(Object) * IOU_{pred}^{truth} = Pr(Class_i) * IOU_{pred}^{truth} \]

此最终的score对probability和bbox的位置进行了综合表示.

Network Design

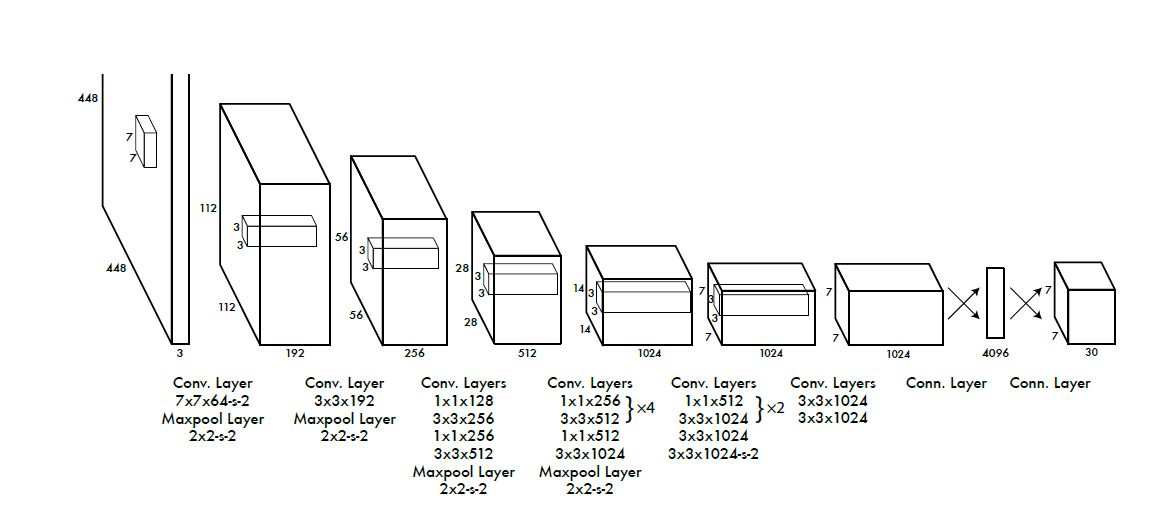
网络结构是以GoogLeNet作为backbone, 先用ConvNet提取feature, 后用fc预测probabilities和coordinates, 结构如下图:

同时作者还提出了一个更快的Fast YOLO以应对极致的速度追求, 此网络主要特点是ConvNet使用了更少的filter, 其余基本与YOLO相同.

Training

对backbone先预训练, 作者了解到Ren et al.的研究, 又加入了4个卷积层和2个fc层.

最终输出probabilities和coordinates, 作者对bbox的w, h用图片的w, h对其归一化, 并将x, y用对所在的grid cell相对位置将其归一化, 所有激活层使用leakyReLU激活:

\[\phi(x) = max(x, 0.1x) \]

使用sum-squared error进行优化. 作者说又由于对每个不包含物体的grid cell太多, 即使其score接近0, 这些不含物体的cell仍会统治导数, 因此作者对其重新加权, 来降低不含物体cell的score(权重\(\lambda_{coord} = 5\)), 并提升含物体cell的score(权重\(\lambda_{noobj} = 0.5\)).

又因为小的变化对小尺寸的bbox影响应该比大尺寸的bbox更大, 因此作者将bbox的w和h用方根表示而非直接使用.

因为上文提到每个cell预测了\(B\)个bbox, 而这些bbox只有一个对物体有响应, 因此作者在loss中也只取score最高的那个bbox而不管此cell中其他的bbox的score.

那么综上考虑, 我们就得到了multi-part loss:

\[\lambda_{\text{coord}}\sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{obj}}[(x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2]\\ + \lambda_{\text{coord}}\sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{obj}}[(\sqrt{w_i} - \sqrt{\hat{w}_i})^2+(\sqrt{h_i} - \sqrt{\hat{h}_i})^2]\\ + \sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{obj}}(C_i - \hat{C}_i)^2\\ +\lambda_{\text{noobj}}\sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{noobj}}(C_i - \hat{C}_i)^2\\ + \sum\limits_{i = 0}^{S^2}\mathbb{1}_i^{\text{obj}}\sum\limits_{c \in \text{classes}}(p_i(c) - \hat{p}_i(c))^2 \]

latex公式用的不熟的朋友就等着哭吧, 这个公式我打了快10分钟, 它大概长这个样子...

$$
\lambda_{\text{coord}}\sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{obj}}[(x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2]\\
+ \lambda_{\text{coord}}\sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{obj}}[(\sqrt{w_i} - \sqrt{\hat{w}_i})^2+(\sqrt{h_i} - \sqrt{\hat{h}_i})^2]\\
+ \sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{obj}}(C_i - \hat{C}_i)^2\\
+\lambda_{\text{noobj}}\sum\limits_{i = 0}^{S^2}\sum\limits_{j = 0}^{B}\mathbb{1}_{i, j}^{\text{noobj}}(C_i - \hat{C}_i)^2\\
+ \sum\limits_{i = 0}^{S^2}\mathbb{1}_i^{\text{obj}}\sum\limits_{c \in \text{classes}}(p_i(c) - \hat{p}_i(c))^2
$$

其中\(\mathbb{1}_i^{\text{obj}}\)在cell\(i\)中有物体时为1, 否则为0, 类似的\(\mathbb{1}_{i, j}^{\text{obj}}\)是指cell\(i\)中的第\(j\)th个bbox对物体有响应时为1, 否则为0.

也就是说loss只惩罚有物体的cell, 和有响应的bbox. 其余的参数细节见原文在此就不再赘述了.

Inference

这种grid设计加强了bbox预测的空间多样性, 通常当一个物体在cell中时的情况很明显, 此网络也只预测该物体的一个box, 当对于一些大的物体或是落在多个cell边界区域时能由多个cell合作产生较好的预测位置. 此外作者还采用NMS来fit此multiple detections.

Limitations of YOLO

因为box有限, 且只有一个box对物体有相应, 当有物体相邻时YOLO表现不够好.

其次, 网络对小bbox中的小变化专注程度有限, 因此在localization上表现不够好.

Experiments

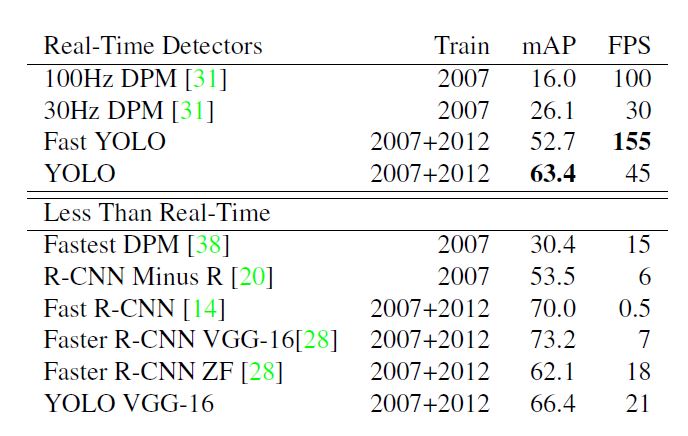
主要针对其他real-time的方法对比, YOLO从速度和质量上有碾压性优势, 对于其他非real-time方法, YOLO也极具竞争力.

VOC 2007 Error Analysis

作者定义了以下几种情况并命名:

• Correct: correct class and IOU > .5
• Localization: correct class, .1 < IOU < .5
• Similar: class is similar, IOU > .1
• Other: class is wrong, IOU > .1
• Background: IOU < .1 for any object

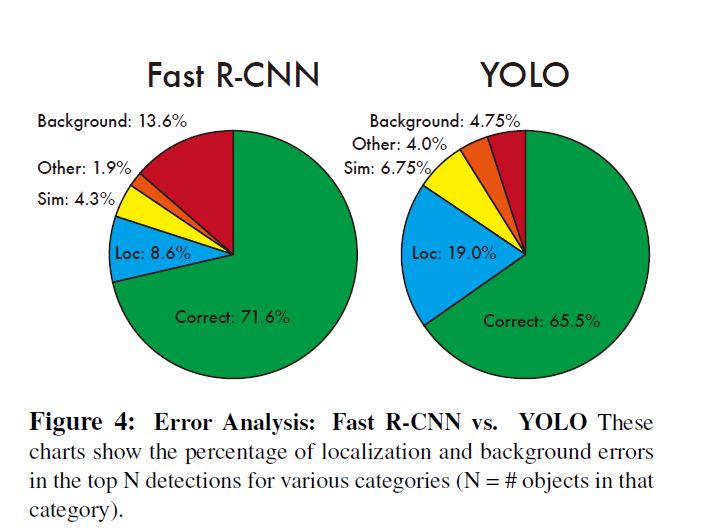
实验结果与Fast R-CNN对比如图:

可以看出, Fast R-CNN在背景分类上会产生更多的错误, YOLO会在localization上产生更多的错误.

Combining Fast R-CNN and YOLO

既然二者有相互补充的地方, 作者就尝试将二者结合, 用YOLO来帮助Fast R-CNN提升背景分类质量. 实验结果证明确实有补充的效果, 但令人遗憾的是因为Fast R-CNN速度较慢, 最终速度表现较差.

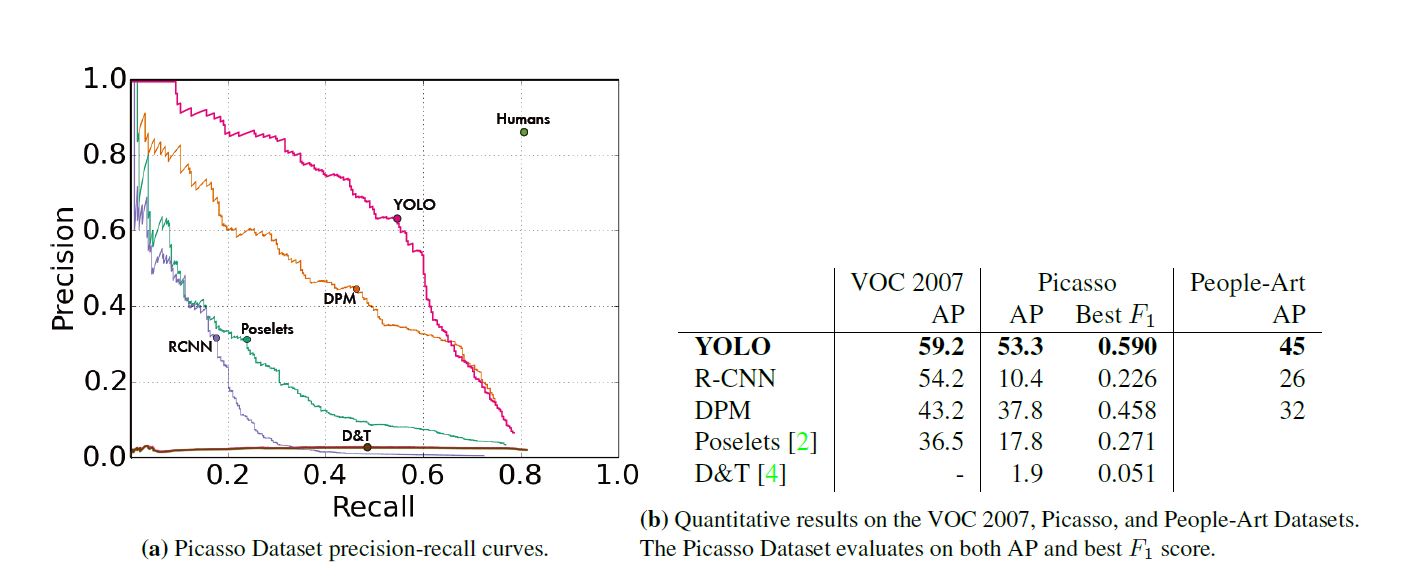
Generalizability: Person Detection in Artwork

作者将若干模型先用VOC预训练, 其后在艺术品集上测试, 得到以下结果, 另附图例.

Conclusion

本文作为one stage模型的开山之作在当时引起了极大轰动, 绕过proposal的过程, 且提出的grid cell思想对以后的影响非凡, 但本方法存在个别问题如临近物体检测效果不好, 后人对该模型改进克服了此困难.